人教版九年级数学上册22.2 二次函数与一元二次方程课件(共40张 用WPS打开)
文档属性
| 名称 | 人教版九年级数学上册22.2 二次函数与一元二次方程课件(共40张 用WPS打开) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 08:07:18 | ||
图片预览




文档简介
(共40张PPT)
22.2
二次函数与一元二次方程
人教版数学九年级上册
3.会利用二次函数的图象求一元二次方程的近似解.
1.探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系.
2.掌握二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系,表述何时方程有两个不等的实根、两个相等的实数和没有实根.
学习目标
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系:
h=20t-5t2,
考虑以下问题:
二次函数与一元二次方程的关系
探究新知
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
O
h
t
15
1
3
∴当球飞行1s或3s时,它的高度为15m.
解:15=20t-5t2,
t2-4t+3=0,
t1=1,t2=3.
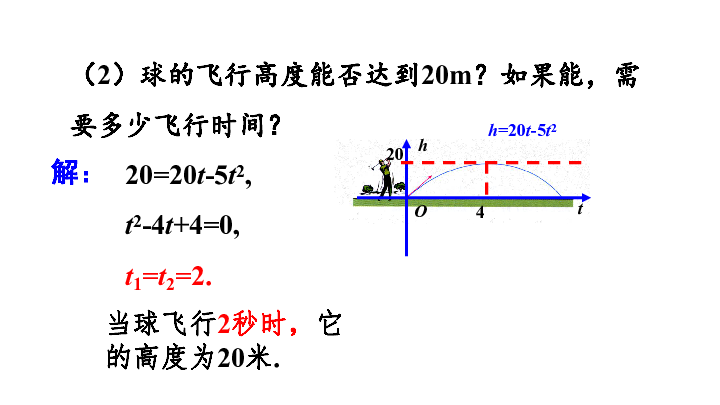
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
O
h
t
20
4
20=20t-5t2,
t2-4t+4=0,
t1=t2=2.
当球飞行2秒时,它的高度为20米.
h=20t-5t2
解:
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
O
h
t
20.5
解:20.5=20t-5t2,
t2-4t+4.1=0,
因为(-4)2-4
×4.1<0,
所以方程无解.
即球的飞行高度达不到20.5米.
h=20t-5t2
(4)球从飞出到落地要用多少时间?
O
h
t
0=20t-5t2,
t2-4t=0,
t1=0,t2=4.
当球飞行0秒和4秒时,它的高度为0米.
即0秒时球地面飞出,4秒时球落回地面.
h=20t-5t2
解:小球飞出时和落地时的高度均为0m,
从上面发现,二次函数y=ax2+bx+c何时为一元二次方程?
一般地,当y取定值且a≠0时,二次函数为一元二次方程.
如:y=5时,则5=ax2+bx+c就是一个一元二次方程.
为一个常数
(定值)
二次函数与一元二次方程关系密切.
例如,已知二次函数y
=
-x2+4x的值为3,求自变量x的值,可以解一元二次方程-x2+4x=3(即x2-4x+3=0).
反过来,解方程x2-4x+3=0
又可以看作已知二次函数
y
=
x2-4x+3
的值为0,求自变量x的值.
已知二次函数中因变量的值,求自变量的值
解一元二次方程
二次函数与一元二次方程的关系(1)
例1
已知二次函数
y=2x2-3x-4的函数值为1,求自变量x的值,可以看作解一元二次方程
2x2-3x-4=1
.
反之,解一元二次方程
2x2-3x-5=0,又可以看作已知二次函数y=2x2-3x-5的函数值为0时自变量x的值.
考点探究1
二次函数与一元二次方程的关系
解之得:x1=-1,x2=2.5
1.
二次函数y=x2-3x+2
,当
x=1
时,y=
;当y=0时,x=
.
2.
抛物线y=4x2-1与y轴的交点坐标为
;与x轴的交点坐标为
.
0
1或2
(0,-1)
(0.5,0)和(-0.5,0)
巩固练习
利用二次函数与x轴的交点讨论一元二次方程的根的情况
【思考】观察思考下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数的值是多少?由此你能得出相应的一元二次方程的根吗?
(1)y=x2+x-2;
(2)y=x2-6x+9;
(3)y=x2-x+1.
探究新知
二次函数图象与x轴的公共点的横坐标是多少?
无公共点
先画出函数图象:
公共点的函数值为
.
0
对应一元二次方程的根是多少?
x1
=-2,
x2
=1.
x1
=x2
=3.
方程无解
有两个不等的实根
有两个相等的实根
没有实数根
由上述问题,你可以得到什么结论呢?
方程ax2+bx+c=0的解就是抛物线y=ax2+bx+c与x轴公共点的横坐标.当抛物线与x轴没有公共点时,对应的方程无实数根.
反过来,由一元二
次方程的根的情况,
也可以确定相应的
二次函数的图象与
x
轴的位置关系.
有两个不等实根
有两个相等实根
没有根
有两个交点
有一个交点
没有交点
△
>
0
△
=
0
△
<
0
一元二次方程ax2+bx+c
=
0
的根
抛物线
y=ax2+bx+c与x轴
若抛物线
y=ax2+bx+c
与
x
轴有交点,则
b2
–
4ac
≥
0
△=
b2
–
4ac
二次函数与一元二次方程的关系(2)
△>0
△=0
△<0
o
x
y
△
=
b2
–
4ac
y=ax2+bx+c
那么a<0时呢?
a>0
1
x
y
O
y
=
x2-6x+9
y
=
x2-x+1
y
=
x2+x-2
观察图象,完成下表:
抛物线与x轴公共点个数
公共点
横坐标
相应的一元二次
方程的根
y
=
x2-x+1
y
=
x2-6x+9
y
=
x2+x-2
0个
1个
2个
x2-x+1=0无解
3
x2-6x+9=0,x1=x2=3
-2,
1
x2+x-2=0,x1=-2,x2=1
二次函数y=ax2+bx+c的图象与x轴交点
一元二次方程ax2+bx+c=0的根
b2-4ac
有两个交点
有两个不相等的实数根
b2-4ac
>
0
有两个重合的交点
有两个相等的实数根
b2-4ac
=
0
没有交点
没有实数根
b2-4ac
<
0
二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0根的关系
例2
已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(1)求证:此抛物线与x轴总有交点;
(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是整数,求正整数m的值.
解:(1)证明:∵m≠0,
∴Δ=[-(m+2)]2-4m×2=m2+4m+4-8m=(m-2)2.
∵(m-2)2≥0,
∴Δ≥0,因此抛物线与x轴总有两个交点;
考点探究2
利用二次函数与一元二次方程的根的关系确定字母的值(范围)
(2)令y=0,则(x-1)(mx-2)=0,即x-1=0或mx-2=0,解得x1=1,x2=
.当m为正整数1或2时,x2的值为整数,因为当m为2时,△=0,抛物线与x轴只有一个交点,所以正整数m的值为1.
已知抛物线y=kx2+2x-1与x轴有两个交点,则k的取值范围是
.
3.
k>-1且k0
巩固练习
例3
如图,丁丁在扔铅球时,铅球沿抛物线
运行,其中x是铅球离初始位置的水平距离,y是铅球离地面的高度.
(1)当铅球离地面的高度为2.1m时,它离初始位置的水平距离是多少?
(2)铅球离地面的高度能否达到2.5m,它离初始位置的水平距离是多少?
(3)铅球离地面的高度能否达
到3m?为什么?
考点探究3
二次函数与一元二次方程关系在实际生活中的应用
探究新知
解:
由抛物线的表达式得
即
解得
即当铅球离地面的高度为2.1m时,它离初始位置的水平距离是1m或5m.
(1)当铅球离地面的高度为2.1m时,它离初始位置的水平距离是多少?
(2)铅球离地面的高度能否达到2.5m,它离初始位置的水平距离是多少?
解:由抛物线的表达式得
即
解得
即当铅球离地面的高度为2.5m时,它离初始位
置的水平距离是3m.
解:由抛物线的表达式得
即
因为
所以方程无实根.
所以铅球离地面的高度不能达到3m.
(3)铅球离地面的高度能否达到3m?为什么?
一元二次方程与二次函数紧密地联系起来了.
如图设水管AB的高出地面2.5m,在B处有一自动旋转的喷水头,喷出的水呈抛物线状,
可用二次函数y=-0.5x2+2x+2.5描述,在所
示的直角坐标系中,求水流的落地点D到
A的距离是多少?
解:根据题意得
-0.5x2+2x+2.5
=
0,
解得x1=5,x2=-1(不合题意舍去)
答:水流的落地点D到A的距离是5m.
分析:根据图象可知,水流的落地点D的纵坐标为0,横坐标即为落地点D到A的距离.
即y=0
.
3.
巩固练习
求一元二次方程
的根的近似值(精确到0.1).
分析:一元二次方程
x?-2x-1=0
的根就是抛物线
y=x?-2x-1
与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫做图象法.
利用二次函数求一元二次方程的近似解
探究新知
解:画出函数
y=x?-2x-1
的图象(如下图),由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.
求一元二次方程
的根的近似值(精确到0.1).
先求位于-1到0之间的根,由图象可估计这个根是-0.4或-0.5,利用计算器进行探索,见下表:
x
…
-0.4
-0.5
…
y
…
-0.04
0.25
…
观察上表可以发现,当x分别取-0.4和-0.5时,对应的y由负变正,可见在-0.5与-0.4之间肯定有一个x使y=0,即有y=x2-2x-1的一个根,题目只要求精确到0.1,这时取x=-0.4或x=-0.5都符合要求.但当x=-0.4时更为接近0.故x1≈-0.4.同理可得另一近似值为x2≈2.4.
利用二次函数的图象求一元二次方程2x2+x-15=0的近似根.
(1)用描点法作二次函数
y=2x2+x-15的图象;
(2)观察估计二次函数
y=2x2+x-15的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个是-3,另一个在2与3之间,分别约为-3和2.5(可将单位长再十等分,借助计算器确定其近似值);
(3)确定方程2x2+x-15=0的解;
由此可知,方程2x2+x-15=0的近似根为:x1≈-3,x2≈2.5.
一元二次方程的图象解法
根据下列表格的对应值:
判断方程
ax2+bx+c
=0
(a≠0,a,b,c为常数)一个解x的范围是(
)
A.
3<
x
<
3.23
B.
3.23
<
x
<
3.24
C.
3.24
3.25
D.
3.25
3.26
x
3.23
3.24
3.25
3.26
y=ax2+bx+c
-0.06
-0.02
0.03
0.09
C
4.
巩固练习
1.已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的近似根为( )
A.x1≈-2.1,x2≈0.1
B.x1≈-2.5,x2≈0.5
C.x1≈-2.9,x2≈0.9
D.x1≈-3,x2≈1
B
课堂检测
基础题
2.若二次函数y=-x2+2x+k的部分图象如图所示,且关于x的一元二次方程-x2+2x+k=0的一个解x1=3,则另一个解x2=
;
-1
3.
一元二次方程
3x2+x-10=0的两个根是x1=-2
,x2=
,那么二次函数
y=
3x2+x-10与x轴的交点坐标是
.
(-2,0)
(
,0)
4.
若一元二次方程
无实根,则抛物线
图象位于(
)
A.x轴上方
B.第一、二、三象限
C.x轴下方
D.第二、三、四象限
A
5.
二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
A.k<3
B.k<3且k≠0
C.k≤3
D.k≤3且k≠0
D
已知函数y=(k-3)x?+2x+1的图象与x轴有交点,求k的取值范围.
解:当k=3时,函数y=2x+1是一次函数.
∵一次函数y=2x+1与x轴有一个交点,
∴k=3;
当k≠3时,y=(k-3)x2+2x+1是二次函数.
∵二次函数y=(k-3)x2+2x+1的图象与x轴有交点,
∴Δ=b2-4ac≥0.
∵b2-4ac=22-4(k-3)=-4k+16,
∴-4k+16≥0.∴k≤4且k≠3.
综上所述,k的取值范围是k≤4.
提升题
某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时距地面
米,与篮框中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行轨迹为抛物线,篮框距地面3米.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,若对方队员乙在甲面前1米处跳起盖帽拦截,已知乙的最大摸高为3.1米,那么他能否获得成功?
拓展题
解:(1)由条件可得到出手点、最高点和篮框的坐标分别为A(0,
),B(4,4),C(7,3),其中B是抛物线的顶点.
设二次函数关系式为y=a(x﹣h)2+k,将点A、B的坐标代入,可得y=﹣
(x
﹣
4)2+4.
将点C的坐标代入上式,得左边=3,右边=
﹣
(7
﹣
4)2+4=3,左边=右边,即点C在抛物线上.所以此球一定能投中.
(1)
建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,若对方队员乙在甲面前1米处跳起盖帽拦截,已知乙的最大摸高为3.1米,那么他能否获得成功?
解:将x=1代入函数关系式,得y=3.
因为3.1>3,所以盖帽能获得成功.
22.2
二次函数与一元二次方程
人教版数学九年级上册
3.会利用二次函数的图象求一元二次方程的近似解.
1.探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系.
2.掌握二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系,表述何时方程有两个不等的实根、两个相等的实数和没有实根.
学习目标
如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系:
h=20t-5t2,
考虑以下问题:
二次函数与一元二次方程的关系
探究新知
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
O
h
t
15
1
3
∴当球飞行1s或3s时,它的高度为15m.
解:15=20t-5t2,
t2-4t+3=0,
t1=1,t2=3.
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
O
h
t
20
4
20=20t-5t2,
t2-4t+4=0,
t1=t2=2.
当球飞行2秒时,它的高度为20米.
h=20t-5t2
解:
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
O
h
t
20.5
解:20.5=20t-5t2,
t2-4t+4.1=0,
因为(-4)2-4
×4.1<0,
所以方程无解.
即球的飞行高度达不到20.5米.
h=20t-5t2
(4)球从飞出到落地要用多少时间?
O
h
t
0=20t-5t2,
t2-4t=0,
t1=0,t2=4.
当球飞行0秒和4秒时,它的高度为0米.
即0秒时球地面飞出,4秒时球落回地面.
h=20t-5t2
解:小球飞出时和落地时的高度均为0m,
从上面发现,二次函数y=ax2+bx+c何时为一元二次方程?
一般地,当y取定值且a≠0时,二次函数为一元二次方程.
如:y=5时,则5=ax2+bx+c就是一个一元二次方程.
为一个常数
(定值)
二次函数与一元二次方程关系密切.
例如,已知二次函数y
=
-x2+4x的值为3,求自变量x的值,可以解一元二次方程-x2+4x=3(即x2-4x+3=0).
反过来,解方程x2-4x+3=0
又可以看作已知二次函数
y
=
x2-4x+3
的值为0,求自变量x的值.
已知二次函数中因变量的值,求自变量的值
解一元二次方程
二次函数与一元二次方程的关系(1)
例1
已知二次函数
y=2x2-3x-4的函数值为1,求自变量x的值,可以看作解一元二次方程
2x2-3x-4=1
.
反之,解一元二次方程
2x2-3x-5=0,又可以看作已知二次函数y=2x2-3x-5的函数值为0时自变量x的值.
考点探究1
二次函数与一元二次方程的关系
解之得:x1=-1,x2=2.5
1.
二次函数y=x2-3x+2
,当
x=1
时,y=
;当y=0时,x=
.
2.
抛物线y=4x2-1与y轴的交点坐标为
;与x轴的交点坐标为
.
0
1或2
(0,-1)
(0.5,0)和(-0.5,0)
巩固练习
利用二次函数与x轴的交点讨论一元二次方程的根的情况
【思考】观察思考下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数的值是多少?由此你能得出相应的一元二次方程的根吗?
(1)y=x2+x-2;
(2)y=x2-6x+9;
(3)y=x2-x+1.
探究新知
二次函数图象与x轴的公共点的横坐标是多少?
无公共点
先画出函数图象:
公共点的函数值为
.
0
对应一元二次方程的根是多少?
x1
=-2,
x2
=1.
x1
=x2
=3.
方程无解
有两个不等的实根
有两个相等的实根
没有实数根
由上述问题,你可以得到什么结论呢?
方程ax2+bx+c=0的解就是抛物线y=ax2+bx+c与x轴公共点的横坐标.当抛物线与x轴没有公共点时,对应的方程无实数根.
反过来,由一元二
次方程的根的情况,
也可以确定相应的
二次函数的图象与
x
轴的位置关系.
有两个不等实根
有两个相等实根
没有根
有两个交点
有一个交点
没有交点
△
>
0
△
=
0
△
<
0
一元二次方程ax2+bx+c
=
0
的根
抛物线
y=ax2+bx+c与x轴
若抛物线
y=ax2+bx+c
与
x
轴有交点,则
b2
–
4ac
≥
0
△=
b2
–
4ac
二次函数与一元二次方程的关系(2)
△>0
△=0
△<0
o
x
y
△
=
b2
–
4ac
y=ax2+bx+c
那么a<0时呢?
a>0
1
x
y
O
y
=
x2-6x+9
y
=
x2-x+1
y
=
x2+x-2
观察图象,完成下表:
抛物线与x轴公共点个数
公共点
横坐标
相应的一元二次
方程的根
y
=
x2-x+1
y
=
x2-6x+9
y
=
x2+x-2
0个
1个
2个
x2-x+1=0无解
3
x2-6x+9=0,x1=x2=3
-2,
1
x2+x-2=0,x1=-2,x2=1
二次函数y=ax2+bx+c的图象与x轴交点
一元二次方程ax2+bx+c=0的根
b2-4ac
有两个交点
有两个不相等的实数根
b2-4ac
>
0
有两个重合的交点
有两个相等的实数根
b2-4ac
=
0
没有交点
没有实数根
b2-4ac
<
0
二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0根的关系
例2
已知关于x的二次函数y=mx2-(m+2)x+2(m≠0).
(1)求证:此抛物线与x轴总有交点;
(2)若此抛物线与x轴总有两个交点,且它们的横坐标都是整数,求正整数m的值.
解:(1)证明:∵m≠0,
∴Δ=[-(m+2)]2-4m×2=m2+4m+4-8m=(m-2)2.
∵(m-2)2≥0,
∴Δ≥0,因此抛物线与x轴总有两个交点;
考点探究2
利用二次函数与一元二次方程的根的关系确定字母的值(范围)
(2)令y=0,则(x-1)(mx-2)=0,即x-1=0或mx-2=0,解得x1=1,x2=
.当m为正整数1或2时,x2的值为整数,因为当m为2时,△=0,抛物线与x轴只有一个交点,所以正整数m的值为1.
已知抛物线y=kx2+2x-1与x轴有两个交点,则k的取值范围是
.
3.
k>-1且k0
巩固练习
例3
如图,丁丁在扔铅球时,铅球沿抛物线
运行,其中x是铅球离初始位置的水平距离,y是铅球离地面的高度.
(1)当铅球离地面的高度为2.1m时,它离初始位置的水平距离是多少?
(2)铅球离地面的高度能否达到2.5m,它离初始位置的水平距离是多少?
(3)铅球离地面的高度能否达
到3m?为什么?
考点探究3
二次函数与一元二次方程关系在实际生活中的应用
探究新知
解:
由抛物线的表达式得
即
解得
即当铅球离地面的高度为2.1m时,它离初始位置的水平距离是1m或5m.
(1)当铅球离地面的高度为2.1m时,它离初始位置的水平距离是多少?
(2)铅球离地面的高度能否达到2.5m,它离初始位置的水平距离是多少?
解:由抛物线的表达式得
即
解得
即当铅球离地面的高度为2.5m时,它离初始位
置的水平距离是3m.
解:由抛物线的表达式得
即
因为
所以方程无实根.
所以铅球离地面的高度不能达到3m.
(3)铅球离地面的高度能否达到3m?为什么?
一元二次方程与二次函数紧密地联系起来了.
如图设水管AB的高出地面2.5m,在B处有一自动旋转的喷水头,喷出的水呈抛物线状,
可用二次函数y=-0.5x2+2x+2.5描述,在所
示的直角坐标系中,求水流的落地点D到
A的距离是多少?
解:根据题意得
-0.5x2+2x+2.5
=
0,
解得x1=5,x2=-1(不合题意舍去)
答:水流的落地点D到A的距离是5m.
分析:根据图象可知,水流的落地点D的纵坐标为0,横坐标即为落地点D到A的距离.
即y=0
.
3.
巩固练习
求一元二次方程
的根的近似值(精确到0.1).
分析:一元二次方程
x?-2x-1=0
的根就是抛物线
y=x?-2x-1
与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫做图象法.
利用二次函数求一元二次方程的近似解
探究新知
解:画出函数
y=x?-2x-1
的图象(如下图),由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.
求一元二次方程
的根的近似值(精确到0.1).
先求位于-1到0之间的根,由图象可估计这个根是-0.4或-0.5,利用计算器进行探索,见下表:
x
…
-0.4
-0.5
…
y
…
-0.04
0.25
…
观察上表可以发现,当x分别取-0.4和-0.5时,对应的y由负变正,可见在-0.5与-0.4之间肯定有一个x使y=0,即有y=x2-2x-1的一个根,题目只要求精确到0.1,这时取x=-0.4或x=-0.5都符合要求.但当x=-0.4时更为接近0.故x1≈-0.4.同理可得另一近似值为x2≈2.4.
利用二次函数的图象求一元二次方程2x2+x-15=0的近似根.
(1)用描点法作二次函数
y=2x2+x-15的图象;
(2)观察估计二次函数
y=2x2+x-15的图象与x轴的交点的横坐标;
由图象可知,图象与x轴有两个交点,其横坐标一个是-3,另一个在2与3之间,分别约为-3和2.5(可将单位长再十等分,借助计算器确定其近似值);
(3)确定方程2x2+x-15=0的解;
由此可知,方程2x2+x-15=0的近似根为:x1≈-3,x2≈2.5.
一元二次方程的图象解法
根据下列表格的对应值:
判断方程
ax2+bx+c
=0
(a≠0,a,b,c为常数)一个解x的范围是(
)
A.
3<
x
<
3.23
B.
3.23
<
x
<
3.24
C.
3.24
D.
3.25
x
3.23
3.24
3.25
3.26
y=ax2+bx+c
-0.06
-0.02
0.03
0.09
C
4.
巩固练习
1.已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的近似根为( )
A.x1≈-2.1,x2≈0.1
B.x1≈-2.5,x2≈0.5
C.x1≈-2.9,x2≈0.9
D.x1≈-3,x2≈1
B
课堂检测
基础题
2.若二次函数y=-x2+2x+k的部分图象如图所示,且关于x的一元二次方程-x2+2x+k=0的一个解x1=3,则另一个解x2=
;
-1
3.
一元二次方程
3x2+x-10=0的两个根是x1=-2
,x2=
,那么二次函数
y=
3x2+x-10与x轴的交点坐标是
.
(-2,0)
(
,0)
4.
若一元二次方程
无实根,则抛物线
图象位于(
)
A.x轴上方
B.第一、二、三象限
C.x轴下方
D.第二、三、四象限
A
5.
二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
A.k<3
B.k<3且k≠0
C.k≤3
D.k≤3且k≠0
D
已知函数y=(k-3)x?+2x+1的图象与x轴有交点,求k的取值范围.
解:当k=3时,函数y=2x+1是一次函数.
∵一次函数y=2x+1与x轴有一个交点,
∴k=3;
当k≠3时,y=(k-3)x2+2x+1是二次函数.
∵二次函数y=(k-3)x2+2x+1的图象与x轴有交点,
∴Δ=b2-4ac≥0.
∵b2-4ac=22-4(k-3)=-4k+16,
∴-4k+16≥0.∴k≤4且k≠3.
综上所述,k的取值范围是k≤4.
提升题
某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时距地面
米,与篮框中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行轨迹为抛物线,篮框距地面3米.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,若对方队员乙在甲面前1米处跳起盖帽拦截,已知乙的最大摸高为3.1米,那么他能否获得成功?
拓展题
解:(1)由条件可得到出手点、最高点和篮框的坐标分别为A(0,
),B(4,4),C(7,3),其中B是抛物线的顶点.
设二次函数关系式为y=a(x﹣h)2+k,将点A、B的坐标代入,可得y=﹣
(x
﹣
4)2+4.
将点C的坐标代入上式,得左边=3,右边=
﹣
(7
﹣
4)2+4=3,左边=右边,即点C在抛物线上.所以此球一定能投中.
(1)
建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,若对方队员乙在甲面前1米处跳起盖帽拦截,已知乙的最大摸高为3.1米,那么他能否获得成功?
解:将x=1代入函数关系式,得y=3.
因为3.1>3,所以盖帽能获得成功.
同课章节目录
