高中数学人教A版必修3第二章2.1.1_2.1.3随机抽样、系统抽样、分层抽样课件(共26张PPT)
文档属性
| 名称 | 高中数学人教A版必修3第二章2.1.1_2.1.3随机抽样、系统抽样、分层抽样课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 605.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
2.1
随机抽样
2.1.1
简单随机抽样
2.1.2
系统抽样
2.1.3
分层抽样
目录
CONTENTS
1
统计学的产生与发展
2
简单随机抽样
3
系统抽样
4
分层抽样
5
随机抽样的应用
统计学的产生与发展
背景知识--你了解统计学吗?
统计一词起源于国情调查,最早意为国情学。
统计:指对某一现象有关的数据的搜集、整理、计算、分析、解释、表述等的活动。
世界统计日:鉴于统计学为世界社会经济、科学技术的发展和进步作出了巨大贡献,2010年第64届联合国大会第90次会议通过决议,每年10月20日为“世界统计日”.
2011年,我国将统计学上升为一级学科.
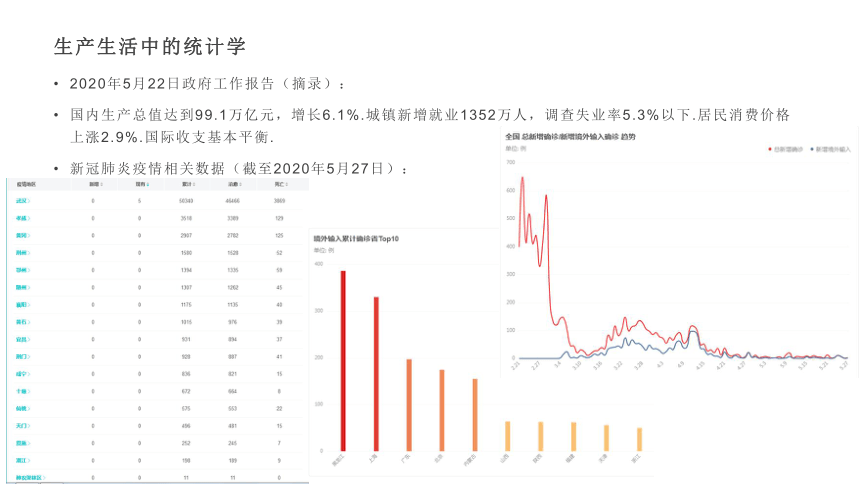
生产生活中的统计学
2020年5月22日政府工作报告(摘录):
国内生产总值达到99.1万亿元,增长6.1%.城镇新增就业1352万人,调查失业率5.3%以下.居民消费价格上涨2.9%.国际收支基本平衡.
新冠肺炎疫情相关数据(截至2020年5月27日):
统计学与我们息息相关
(1)社会调查
(2)广告投放
(3)教学研究
(4)食品安全
(5)水质监测
(6)交通运输
(7)运营管理
(8)国防安全
......
简单随机抽样
背景问题:
假设你是一名食品卫生工作人员,要对某食品店内的一批小包装饼干进行卫生达标检验,你准备怎样做?
显然,你只能从中抽取一定数量的饼干作为检验的样本.(为什么?)
那么,应该怎样获取样本呢?
概念引入
简单随机抽样:一般地,设一个总体含有N个个体,从中逐个不放回地抽取n个个体作为样本(n≤N),如果每次抽取时总体内的各个个体被抽到的机会都相等,就把这种抽样方法叫做简单随机抽样.
简单随机抽样
抽签法(抓阄法)
随机数法
简单随机抽样--抽签法(抓阄法)
抽签法(抓阄法)的几个步骤和注意点:
(1)把总体中的N个个体编号,把号码写在号签上;(注意:编号不一定要用数字,用A,B,C,D等字母符号也可以)
(2)将号签放在不透明的容器中,搅拌均匀;
(3)每次不放回地从中抽取一个,抽取n次,得到一个容量为n的样本.
思考:
(1)抽签法有何优点和缺点?
(2)当总体中的个体数很多的时,用抽签法方便吗?
简单随机抽样--随机数法
常见的产生随机数的方式:随机数表,随机数骰子,计算机产生的随机数。
生活情境:
要考察某学校食堂的15元套餐是否符合卫生检疫标准,现需要从800份套餐中抽取60份进行检验.
第一步:编号.将800份套餐编号为000,001,002,...,798,799
第二步:任选一个读数起点.下图为随机数表第6行至第10行,我们不妨选取第8行第7列的数字7作为读数起点.
第三步:任选一个方向开始读数.我们不妨向右读数,第一个三位数是785,由于785<799,说明785在总体内,将该编号取出;继续向右读,得到916,由于916>799,不在总体内,将其去掉.按照这种方法继续向右读,直到取出60个符合要求的编号,这样就得到了一个容量为60的样本.
简单随机抽样--随机数法
思考:
(1)随机数法对编号的形式有何要求?
答:通常与总体数量的数值位数保持一致.
(2)为什么要从000开始编号?能否从001考试编号?
答:从000开始,主要是为了便于编号;也可以从001开始编号,但读数可能会比较繁琐、耗时.
(3)读数完成,抽样过程就算完成了吗?
答:读数完成,表明我们抽取哪些个体的目标明确了,接下来还需要到总体中按取出样本的编号,将实际物品取出,这才算抽样完成了.
对简单随机抽样的评价
(1)总体容量不大时,操作简单易行,且行之有效;
(2)总体容量大较大时,编号工作量太大,利用随机数法也并不方便快捷;
(3)“搅拌均匀”往往比较困难,特别是在总体容量较大的时候,样本代表性较差.
系统抽样
系统抽样的基本步骤
背景问题:为了解高一学生对学校数学教学的评价,拟从高一500名学生中抽取50名学生进行调查,除了用简单随机抽样的方式之外,你能否设计其他抽取样本的方法?
问题抽象:从容量为N的总体中抽取容量为n的样本.
按一定规则抽取样本.
04
通常利用l+k,l+2k,l+3k,...这种不断添加分段间隔的方式确定样本编号.本题最终选取的编号为:9,19,29,39,49,...,499
第一段中随机抽样确定第一个个体编号.
03
在第一组10名同学中,采用简单随机抽样(抽签法或随机数法),确定第一个个体的编号l(l≤k).假设抽到的是9.
确定分段间隔k.
02
10人一组(即k=10),将500名学生分为50组.
即:第1组10名学生的编号为1~10,第2组学生的编号为11~20,以此类推.
将总体的N个个体编号.
01
将500名学生按1,2,3,...,500进行编号.
系统抽样的概念
将总体平均分成几部分,然后按照一定的规则,从每一部分抽取一个个体作为样本,这种抽样的方法叫做系统抽样。
系统抽样,实质上是将问题分块处理,将复杂问题简单化,这体现了数学“化繁为简”的转化思想.
对系统抽样的几点思考
1.系统抽样一定要等距离抽取样本吗?
答:不一定要等距抽样,可以非等距抽样,但仍要按照一定的规则.
2.前面的实际问题中,如果学生人数为503人,仍要采用系统抽样,该如何处理?
答:先用简单随机抽样剔除3个个体,再采用系统抽样.
3.与简单随机抽样相比,系统抽样有何优点和不足?它能提高样本的代表性吗?举例说明。
答:对于容量较大的总体,系统抽样更加便于操作。但系统抽样有时又会因为编号变化的周期性,导致样本代表性差。例如:男生女生交替排成一路纵队进行编号,用系统抽样,可能会导致抽到的全部为男生或全部为女生;如果将全班同学按体重顺序进行编号,此时用系统抽样是合理的。另外,实际生产生活中,对生产线上的产品进行检测时,往往也采用系统抽样,便于操作。
分层抽样
分层抽样--探究问题
某地区有高中生2400人,初中生10900人,小学生11000人.教育部分为了解该地区学生近视情况及其形成原因,需从中抽取1%的学生进行调查,你认为应当怎样抽取样本?
思考一:
哪些因素可能影响学生的视力?设计抽样方法时需要考虑这些因素吗?
采用的方法:
将所有学生分为高中、初中、小学三部分分别抽样,因三部分人数差异大,还需考虑他们在样本中所占的比例。样本容量与总体中个体数的比是1:100,因此,样本中各部分包含的个体数为24,109,110.在三个部分内部,可采用系统抽样的方式得到各个部分的样本。最后,将上述样本合在一起,即为最终样本.
思考二:
为什么要这样取各个学段的个体数?
分层抽样的概念
一般地,在抽样时,将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,将各层取出的个体合在一起作为样本,这种抽样方法是一种分层抽样.
4、分层抽样的一般步骤:
(1)将总体按一定的标准分层;
(2)计算各层的个体数与总体的个体数的比;
(3)按各层个体数占总体的个体数的比确定各层应抽取的样本容量;
(5)综合每层抽样,组成样本.
(4)在每一层进行抽样;(可用简单随机抽样或系统抽样)
开始
分层
计算比
定层抽取容量
抽样
组样
结束
简单随机抽样、系统抽样、分层抽样的比较
类别
共同点
各自特点
联系
适用范围
简单随机抽样
(1)抽样过程中每个个体被抽到的可能性相等
(2)每次抽出个体后不再将它放回,即不放回抽样
从总体中逐个抽取
总体个数较少
系统
抽样
将总体平均分成几部分,按预先制定的规则在各部分抽取
在起始部分时采用简单随机抽样
总体个数较多
分层
抽样
将总体分成几层,分层进行抽取
各层抽样时采用简单随机抽样或系统抽样
总体由差异明显的几部分组成
1、下列问题采用怎样的抽样方法比较合理:
①从10台冰箱中抽取3台进行质量检查;
③某学校有160名教职工,其中教师120名,行政人员16名,后勤人员24名。为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本。
分层抽样
系统抽样
简单随机抽样
②某电影院有32排座位,每排有40个座位,座位号为1~40。
有一次报告会坐满了听众,会议结束后为听取意见,需留下32名听众进行座谈;
四、针对性练习
2、从2005个编号中抽取20个号码入样,采用系统抽样的方法,则抽样的间隔为(
)
A、99
B、99.5
C、100
D、100.5
C
3、某小礼堂有25排座位,每排20个座位,一次心理学讲座,礼堂中坐满了学生,会后为了了解有关情况,留下座位号是15的所有25名学生进行测试,这里运用的是
抽样方法。
系统
4、采用系统抽样从个体数为83的总体中抽取一个样本容量为10的样本,那么每个个体被抽到的可能性为
_________.
5、从2004名学生中选取50名组成参观团,若采用下面的方法选取:先用简单随机抽样从2004人中剔除4人,剩下的2000个再按系统抽样的方法进行,则每人入选的机会(
)
A.不全相等
B.均不相等
C.都相等
D.无法确定
C
6、某中学高一年级有学生600人,高二年级有学生450人,高三年级有学生750人,每个学生被抽到的可能性均为0.2,若该校取一个容量为n的样本,则n=_____
360
7、某校有500名学生,其中O型血的有200人,A型血的人有125人,B型血的有125人,AB型血的有50人,为了研究血型与色弱的关系,要从中抽取一个20人的样本,按分层抽样,O型血应抽取的人数为____人
8
谢谢观看!
2.1
随机抽样
2.1.1
简单随机抽样
2.1.2
系统抽样
2.1.3
分层抽样
目录
CONTENTS
1
统计学的产生与发展
2
简单随机抽样
3
系统抽样
4
分层抽样
5
随机抽样的应用
统计学的产生与发展
背景知识--你了解统计学吗?
统计一词起源于国情调查,最早意为国情学。
统计:指对某一现象有关的数据的搜集、整理、计算、分析、解释、表述等的活动。
世界统计日:鉴于统计学为世界社会经济、科学技术的发展和进步作出了巨大贡献,2010年第64届联合国大会第90次会议通过决议,每年10月20日为“世界统计日”.
2011年,我国将统计学上升为一级学科.
生产生活中的统计学
2020年5月22日政府工作报告(摘录):
国内生产总值达到99.1万亿元,增长6.1%.城镇新增就业1352万人,调查失业率5.3%以下.居民消费价格上涨2.9%.国际收支基本平衡.
新冠肺炎疫情相关数据(截至2020年5月27日):
统计学与我们息息相关
(1)社会调查
(2)广告投放
(3)教学研究
(4)食品安全
(5)水质监测
(6)交通运输
(7)运营管理
(8)国防安全
......
简单随机抽样
背景问题:
假设你是一名食品卫生工作人员,要对某食品店内的一批小包装饼干进行卫生达标检验,你准备怎样做?
显然,你只能从中抽取一定数量的饼干作为检验的样本.(为什么?)
那么,应该怎样获取样本呢?
概念引入
简单随机抽样:一般地,设一个总体含有N个个体,从中逐个不放回地抽取n个个体作为样本(n≤N),如果每次抽取时总体内的各个个体被抽到的机会都相等,就把这种抽样方法叫做简单随机抽样.
简单随机抽样
抽签法(抓阄法)
随机数法
简单随机抽样--抽签法(抓阄法)
抽签法(抓阄法)的几个步骤和注意点:
(1)把总体中的N个个体编号,把号码写在号签上;(注意:编号不一定要用数字,用A,B,C,D等字母符号也可以)
(2)将号签放在不透明的容器中,搅拌均匀;
(3)每次不放回地从中抽取一个,抽取n次,得到一个容量为n的样本.
思考:
(1)抽签法有何优点和缺点?
(2)当总体中的个体数很多的时,用抽签法方便吗?
简单随机抽样--随机数法
常见的产生随机数的方式:随机数表,随机数骰子,计算机产生的随机数。
生活情境:
要考察某学校食堂的15元套餐是否符合卫生检疫标准,现需要从800份套餐中抽取60份进行检验.
第一步:编号.将800份套餐编号为000,001,002,...,798,799
第二步:任选一个读数起点.下图为随机数表第6行至第10行,我们不妨选取第8行第7列的数字7作为读数起点.
第三步:任选一个方向开始读数.我们不妨向右读数,第一个三位数是785,由于785<799,说明785在总体内,将该编号取出;继续向右读,得到916,由于916>799,不在总体内,将其去掉.按照这种方法继续向右读,直到取出60个符合要求的编号,这样就得到了一个容量为60的样本.
简单随机抽样--随机数法
思考:
(1)随机数法对编号的形式有何要求?
答:通常与总体数量的数值位数保持一致.
(2)为什么要从000开始编号?能否从001考试编号?
答:从000开始,主要是为了便于编号;也可以从001开始编号,但读数可能会比较繁琐、耗时.
(3)读数完成,抽样过程就算完成了吗?
答:读数完成,表明我们抽取哪些个体的目标明确了,接下来还需要到总体中按取出样本的编号,将实际物品取出,这才算抽样完成了.
对简单随机抽样的评价
(1)总体容量不大时,操作简单易行,且行之有效;
(2)总体容量大较大时,编号工作量太大,利用随机数法也并不方便快捷;
(3)“搅拌均匀”往往比较困难,特别是在总体容量较大的时候,样本代表性较差.
系统抽样
系统抽样的基本步骤
背景问题:为了解高一学生对学校数学教学的评价,拟从高一500名学生中抽取50名学生进行调查,除了用简单随机抽样的方式之外,你能否设计其他抽取样本的方法?
问题抽象:从容量为N的总体中抽取容量为n的样本.
按一定规则抽取样本.
04
通常利用l+k,l+2k,l+3k,...这种不断添加分段间隔的方式确定样本编号.本题最终选取的编号为:9,19,29,39,49,...,499
第一段中随机抽样确定第一个个体编号.
03
在第一组10名同学中,采用简单随机抽样(抽签法或随机数法),确定第一个个体的编号l(l≤k).假设抽到的是9.
确定分段间隔k.
02
10人一组(即k=10),将500名学生分为50组.
即:第1组10名学生的编号为1~10,第2组学生的编号为11~20,以此类推.
将总体的N个个体编号.
01
将500名学生按1,2,3,...,500进行编号.
系统抽样的概念
将总体平均分成几部分,然后按照一定的规则,从每一部分抽取一个个体作为样本,这种抽样的方法叫做系统抽样。
系统抽样,实质上是将问题分块处理,将复杂问题简单化,这体现了数学“化繁为简”的转化思想.
对系统抽样的几点思考
1.系统抽样一定要等距离抽取样本吗?
答:不一定要等距抽样,可以非等距抽样,但仍要按照一定的规则.
2.前面的实际问题中,如果学生人数为503人,仍要采用系统抽样,该如何处理?
答:先用简单随机抽样剔除3个个体,再采用系统抽样.
3.与简单随机抽样相比,系统抽样有何优点和不足?它能提高样本的代表性吗?举例说明。
答:对于容量较大的总体,系统抽样更加便于操作。但系统抽样有时又会因为编号变化的周期性,导致样本代表性差。例如:男生女生交替排成一路纵队进行编号,用系统抽样,可能会导致抽到的全部为男生或全部为女生;如果将全班同学按体重顺序进行编号,此时用系统抽样是合理的。另外,实际生产生活中,对生产线上的产品进行检测时,往往也采用系统抽样,便于操作。
分层抽样
分层抽样--探究问题
某地区有高中生2400人,初中生10900人,小学生11000人.教育部分为了解该地区学生近视情况及其形成原因,需从中抽取1%的学生进行调查,你认为应当怎样抽取样本?
思考一:
哪些因素可能影响学生的视力?设计抽样方法时需要考虑这些因素吗?
采用的方法:
将所有学生分为高中、初中、小学三部分分别抽样,因三部分人数差异大,还需考虑他们在样本中所占的比例。样本容量与总体中个体数的比是1:100,因此,样本中各部分包含的个体数为24,109,110.在三个部分内部,可采用系统抽样的方式得到各个部分的样本。最后,将上述样本合在一起,即为最终样本.
思考二:
为什么要这样取各个学段的个体数?
分层抽样的概念
一般地,在抽样时,将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,将各层取出的个体合在一起作为样本,这种抽样方法是一种分层抽样.
4、分层抽样的一般步骤:
(1)将总体按一定的标准分层;
(2)计算各层的个体数与总体的个体数的比;
(3)按各层个体数占总体的个体数的比确定各层应抽取的样本容量;
(5)综合每层抽样,组成样本.
(4)在每一层进行抽样;(可用简单随机抽样或系统抽样)
开始
分层
计算比
定层抽取容量
抽样
组样
结束
简单随机抽样、系统抽样、分层抽样的比较
类别
共同点
各自特点
联系
适用范围
简单随机抽样
(1)抽样过程中每个个体被抽到的可能性相等
(2)每次抽出个体后不再将它放回,即不放回抽样
从总体中逐个抽取
总体个数较少
系统
抽样
将总体平均分成几部分,按预先制定的规则在各部分抽取
在起始部分时采用简单随机抽样
总体个数较多
分层
抽样
将总体分成几层,分层进行抽取
各层抽样时采用简单随机抽样或系统抽样
总体由差异明显的几部分组成
1、下列问题采用怎样的抽样方法比较合理:
①从10台冰箱中抽取3台进行质量检查;
③某学校有160名教职工,其中教师120名,行政人员16名,后勤人员24名。为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本。
分层抽样
系统抽样
简单随机抽样
②某电影院有32排座位,每排有40个座位,座位号为1~40。
有一次报告会坐满了听众,会议结束后为听取意见,需留下32名听众进行座谈;
四、针对性练习
2、从2005个编号中抽取20个号码入样,采用系统抽样的方法,则抽样的间隔为(
)
A、99
B、99.5
C、100
D、100.5
C
3、某小礼堂有25排座位,每排20个座位,一次心理学讲座,礼堂中坐满了学生,会后为了了解有关情况,留下座位号是15的所有25名学生进行测试,这里运用的是
抽样方法。
系统
4、采用系统抽样从个体数为83的总体中抽取一个样本容量为10的样本,那么每个个体被抽到的可能性为
_________.
5、从2004名学生中选取50名组成参观团,若采用下面的方法选取:先用简单随机抽样从2004人中剔除4人,剩下的2000个再按系统抽样的方法进行,则每人入选的机会(
)
A.不全相等
B.均不相等
C.都相等
D.无法确定
C
6、某中学高一年级有学生600人,高二年级有学生450人,高三年级有学生750人,每个学生被抽到的可能性均为0.2,若该校取一个容量为n的样本,则n=_____
360
7、某校有500名学生,其中O型血的有200人,A型血的人有125人,B型血的有125人,AB型血的有50人,为了研究血型与色弱的关系,要从中抽取一个20人的样本,按分层抽样,O型血应抽取的人数为____人
8
谢谢观看!
