人教版八年级下册数学:17.1 勾股定理(三) -----在数轴上表示无理数课件(共15张PPT)
文档属性
| 名称 | 人教版八年级下册数学:17.1 勾股定理(三) -----在数轴上表示无理数课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-21 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
17.1
勾股定理(三)
-----在数轴上表示无理数
数学人教版
八年级下
复习导入
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
1.说一说勾股定理的内容?
2.如果直角三角形的两边长分别为3和4,那么第三边的长是________.
①4为直角边:
②4为斜边:
3.一个正方形的边长为1,则其对角线长为_____
?
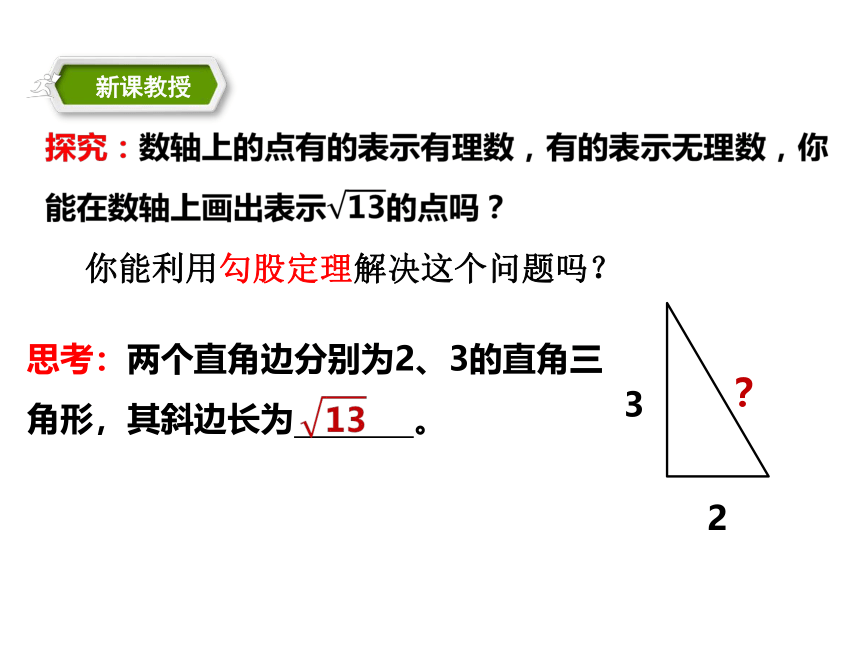
思考:两个直角边分别为2、3的直角三角形,其斜边长为
。
2
3
?
你能利用勾股定理解决这个问题吗?
新课教授
0
1
2
3
4
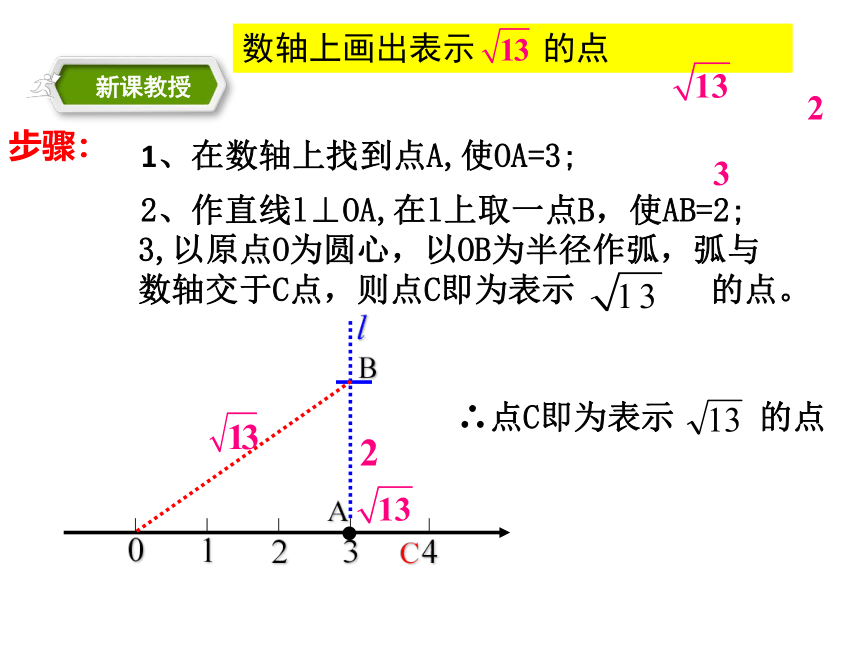
步骤:
l
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
新课教授
练一练
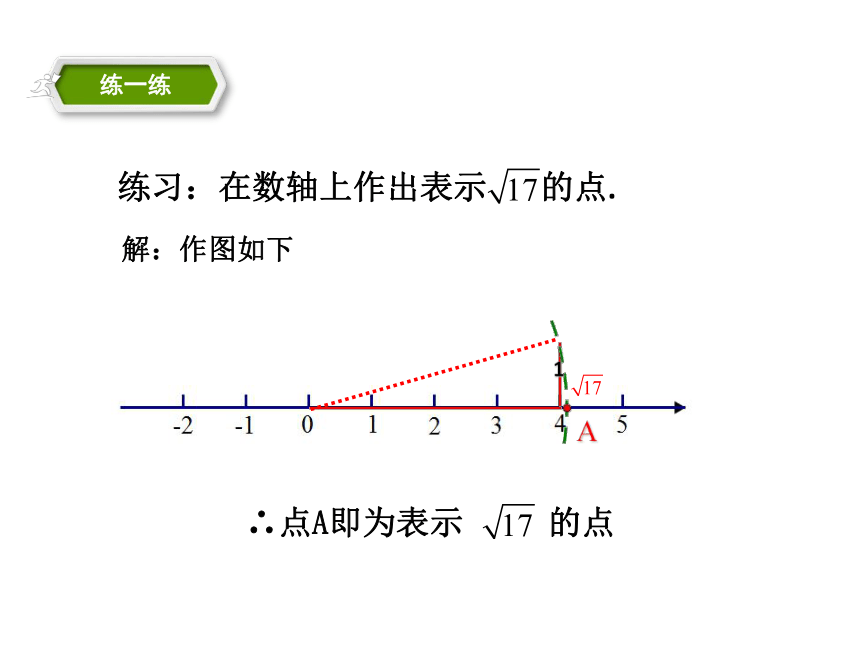
练习:在数轴上作出表示
的点.
1
A
解:作图如下
?
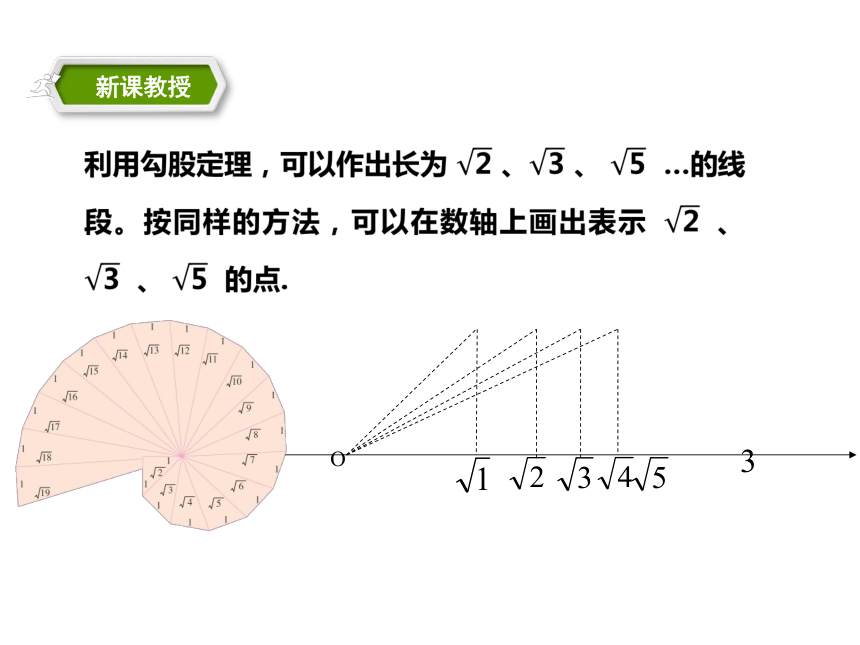
新课教授
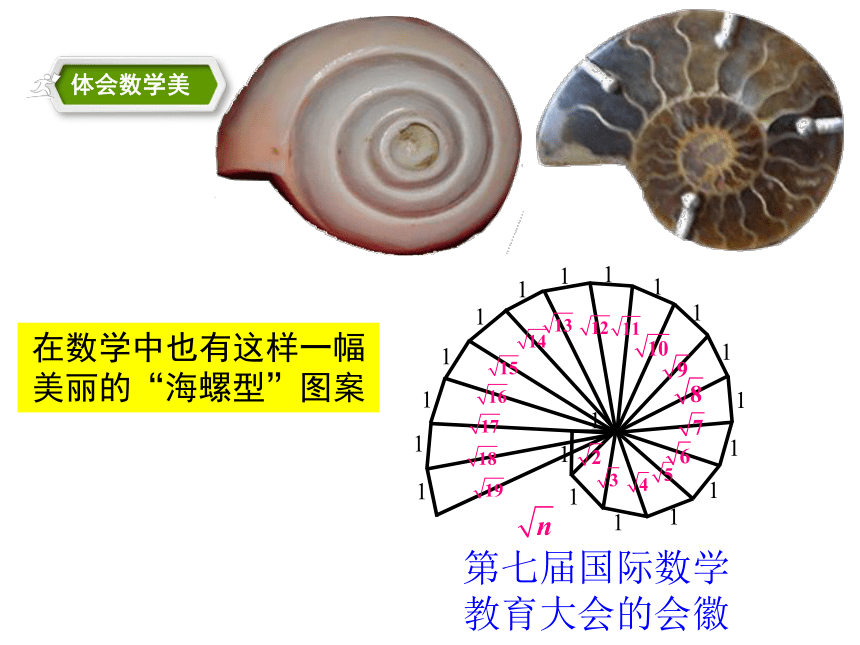
在数学中也有这样一幅美丽的“海螺型”图案
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
第七届国际数学
教育大会的会徽
1
体会数学美
知识巩固
1.如图,正方形网格中,每个小正方形的边长为1,则在网格上的三角形ABC中,边长为无理数的边数有(
)
A.0条
B.1条
C.2条
D.3条
D
利用勾股定理解决问题:
C
知识巩固
知识巩固
4.如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△BAC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE.依此类推,则第2018个等腰直角三角形的斜边长是_______.
21009
知识巩固
知识运用
已知:如图,在Rt△ABC
和Rt△A′B′C′中,∠C=∠C′=90°,AB=A′B′,AC=A′C′.
求证:△ABC≌△A′B′C′.
证明:在Rt△ABC
和Rt△A′B′C′中,
∠C=∠C′=90°,根据勾股定理,得
∴△ABC≌△A′B′C′(SSS).
∵AB=A′B′,AC=A′C′,
∴BC=B′C′.
利用勾股定理证明:斜边和一条直角边
对应相等的两个直角三角形全等。
荷花问题
平平湖水清可鉴,
面上半尺生红莲;
出泥不染亭亭立,
忽被强风吹一边;
渔人观看忙向前,
花离原位二尺远;
能算诸君请解题,
湖水如何知深浅.
0.5
x
x+0.5
2
答:湖水深3.75尺.
可用勾股定理建立方程.
课堂小结
今天我们学习了哪些知识?
你能说说勾股定理在今天学习中的应用吗?
布置作业
1、教材P28页习题17.1第6题.
2、完成课堂小测
?
17.1
勾股定理(三)
-----在数轴上表示无理数
数学人教版
八年级下
复习导入
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
1.说一说勾股定理的内容?
2.如果直角三角形的两边长分别为3和4,那么第三边的长是________.
①4为直角边:
②4为斜边:
3.一个正方形的边长为1,则其对角线长为_____
?
思考:两个直角边分别为2、3的直角三角形,其斜边长为
。
2
3
?
你能利用勾股定理解决这个问题吗?
新课教授
0
1
2
3
4
步骤:
l
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
新课教授
练一练
练习:在数轴上作出表示
的点.
1
A
解:作图如下
?
新课教授
在数学中也有这样一幅美丽的“海螺型”图案
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
第七届国际数学
教育大会的会徽
1
体会数学美
知识巩固
1.如图,正方形网格中,每个小正方形的边长为1,则在网格上的三角形ABC中,边长为无理数的边数有(
)
A.0条
B.1条
C.2条
D.3条
D
利用勾股定理解决问题:
C
知识巩固
知识巩固
4.如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△BAC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE.依此类推,则第2018个等腰直角三角形的斜边长是_______.
21009
知识巩固
知识运用
已知:如图,在Rt△ABC
和Rt△A′B′C′中,∠C=∠C′=90°,AB=A′B′,AC=A′C′.
求证:△ABC≌△A′B′C′.
证明:在Rt△ABC
和Rt△A′B′C′中,
∠C=∠C′=90°,根据勾股定理,得
∴△ABC≌△A′B′C′(SSS).
∵AB=A′B′,AC=A′C′,
∴BC=B′C′.
利用勾股定理证明:斜边和一条直角边
对应相等的两个直角三角形全等。
荷花问题
平平湖水清可鉴,
面上半尺生红莲;
出泥不染亭亭立,
忽被强风吹一边;
渔人观看忙向前,
花离原位二尺远;
能算诸君请解题,
湖水如何知深浅.
0.5
x
x+0.5
2
答:湖水深3.75尺.
可用勾股定理建立方程.
课堂小结
今天我们学习了哪些知识?
你能说说勾股定理在今天学习中的应用吗?
布置作业
1、教材P28页习题17.1第6题.
2、完成课堂小测
?
