沪科版数学九年级下册:26.3用频率估计概率 课件(共16张PPT)
文档属性
| 名称 | 沪科版数学九年级下册:26.3用频率估计概率 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 681.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-28 10:50:19 | ||
图片预览



文档简介
(共16张PPT)
26.3
用频率估计概率
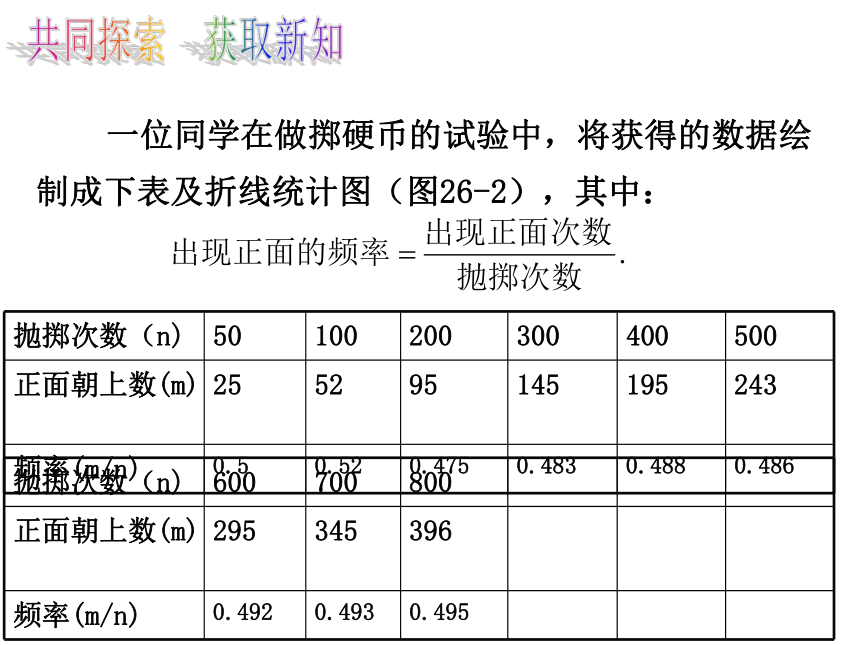
一位同学在做掷硬币的试验中,将获得的数据绘制成下表及折线统计图(图26-2),其中:
抛掷次数(n)
50
100
200
300
400
500
正面朝上数(m)
25
52
95
145
195
243
频率(m/n)
0.5
0.52
0.475
0.483
0.488
0.486
抛掷次数(n)
600
700
800
正面朝上数(m)
295
345
396
频率(m/n)
0.492
0.493
0.495
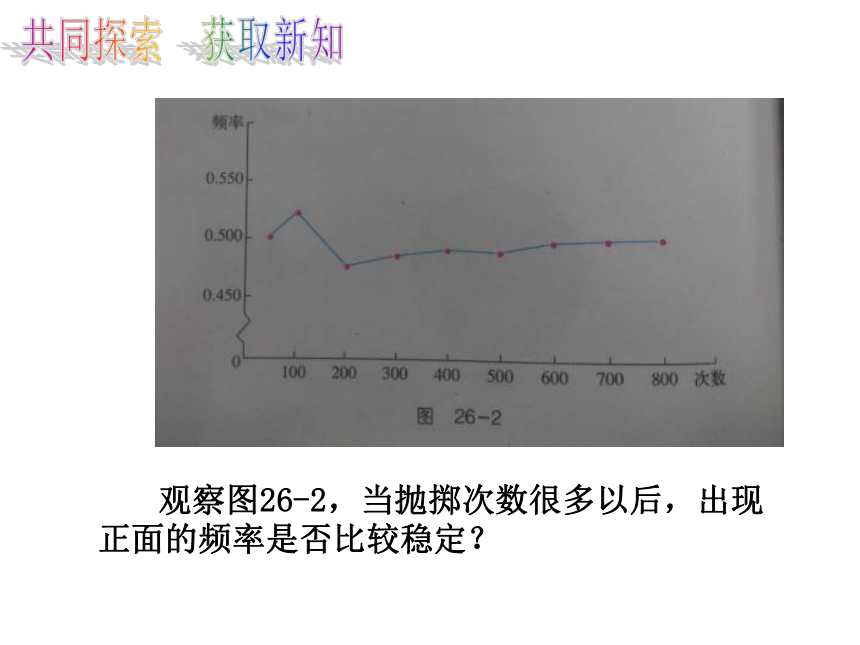
观察图26-2,当抛掷次数很多以后,出现正面的频率是否比较稳定?
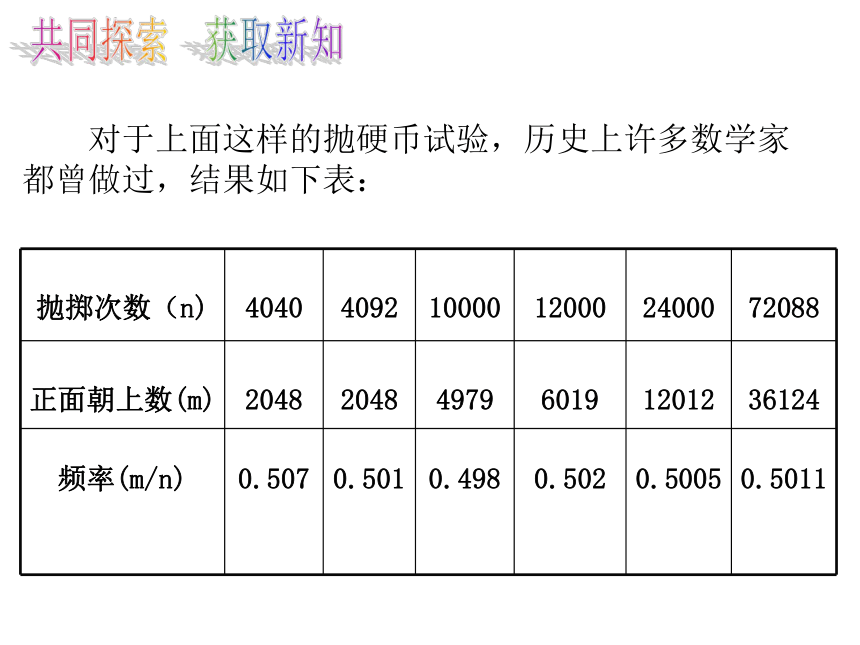
对于上面这样的抛硬币试验,历史上许多数学家都曾做过,结果如下表:
抛掷次数(n)
4040
4092
10000
12000
24000
72088
正面朝上数(m)
2048
2048
4979
6019
12012
36124
频率(m/n)
0.507
0.501
0.498
0.502
0.5005
0.5011
从上面试验中我们可以发现,在重复抛掷一枚硬币时,出现正面和出现反面的频率都在0.5附近波动的幅度会越来越小,呈现一定的稳定性,出现正面和出现反面的频率都逐渐稳定到常数0.5.
这样,我们用随机事件发生的频率逐渐稳定到稳定的常数来刻画它发生的可能性的大小,0.5就作为多次抛掷硬币后出现正面或反面这个随机事件发生的概率.
下面再看两个例子.
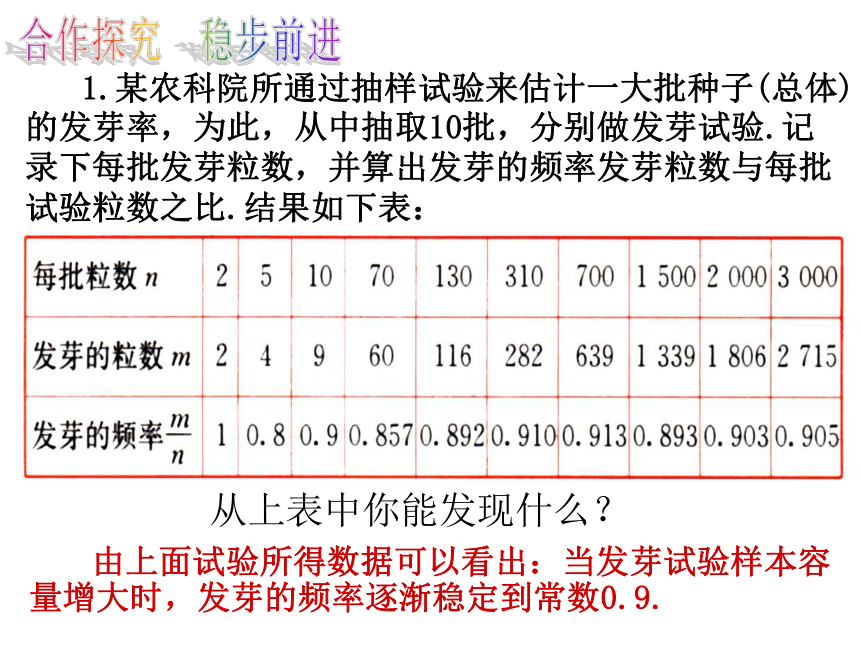
从上表中你能发现什么?
1.某农科院所通过抽样试验来估计一大批种子(总体)的发芽率,为此,从中抽取10批,分别做发芽试验.记录下每批发芽粒数,并算出发芽的频率发芽粒数与每批试验粒数之比.结果如下表:
由上面试验所得数据可以看出:当发芽试验样本容量增大时,发芽的频率逐渐稳定到常数0.9.
2.某乒乓球生产厂,从最近生产的一大批乒乓球中抽取6批进行质量检测,结果如下表:
由上面检测所得数据可以看出:当质量检测样本容量增大时,优等品的频率逐渐稳定常数到0.95.
从上表中你能发现什么?
由上面两个例子说明,一般随机事件具有一个极为重要的特性——频率的稳定性,即在大次数重复试验中,随机事件发生的频率总是稳定到一个常数.我们就用频率所稳定到的这个常数来衡量该随机事件发生可能性的大小.于是,就认为第1个例子中种子发芽的概率为0.9,第2个例子中乒乓球优等品的概率为0.95.
随机事件及其概率
一般地,在大量重复进行同一试验时,随机事件A发生的频率
(n为实验的次数,m是事件发生的频数)总是接近于某个常数P。于是,我们用P这个常数表示随机事件A发生的概率,记做
这样,求一个随机事件概率的基本方法可以是:通过大量重复试验,用这个随机事件发生的频率作为它的概率的估计值.
某农科所在相同条件下做了某作物种子发芽率的实验,结果如下表所示:
0.94
0.94
0.94
0.96
0.87
0.89
0.89
0.9
0.9
0.98
种子个数
发芽种子个数
发芽种子频率
100
94
200
187
300
282
400
338
500
435
600
530
700
624
800
718
900
814
1000
981
一般地,1
000千克种子中大约有多少是不能发芽的?
解:
这批种子的发芽的频率稳定在0.9即种子发芽的概率为90%,不发芽的概率为0.1,机不发芽率为10%.
所以:
1000×10%=100千克
答:1000千克种子大约有100千克是不能发芽的.
某射手进行射击,结果如下表所示:
填表:
(1)这个射手射击一次,击中靶心的概率是多少?
0.5
(2)这射手射击1600次,击中靶心的次数是 。
800
0.65
0.58
0.52
0.51
0.55
射击次数n
20
100
200
500
800
击中靶心次数m
13
58
104
255
404
击中靶心频率m/n
本节课我们学习了什么知识?你有哪些收获?还有什么疑惑吗?
必做题:书本P109第1,2,3题
选做题:书本P109数学园地
现实是此岸,成功是彼岸,中间隔着湍急的河流,兴趣便是河上的桥,只要行动就可以通过.
—克雷洛夫
26.3
用频率估计概率
一位同学在做掷硬币的试验中,将获得的数据绘制成下表及折线统计图(图26-2),其中:
抛掷次数(n)
50
100
200
300
400
500
正面朝上数(m)
25
52
95
145
195
243
频率(m/n)
0.5
0.52
0.475
0.483
0.488
0.486
抛掷次数(n)
600
700
800
正面朝上数(m)
295
345
396
频率(m/n)
0.492
0.493
0.495
观察图26-2,当抛掷次数很多以后,出现正面的频率是否比较稳定?
对于上面这样的抛硬币试验,历史上许多数学家都曾做过,结果如下表:
抛掷次数(n)
4040
4092
10000
12000
24000
72088
正面朝上数(m)
2048
2048
4979
6019
12012
36124
频率(m/n)
0.507
0.501
0.498
0.502
0.5005
0.5011
从上面试验中我们可以发现,在重复抛掷一枚硬币时,出现正面和出现反面的频率都在0.5附近波动的幅度会越来越小,呈现一定的稳定性,出现正面和出现反面的频率都逐渐稳定到常数0.5.
这样,我们用随机事件发生的频率逐渐稳定到稳定的常数来刻画它发生的可能性的大小,0.5就作为多次抛掷硬币后出现正面或反面这个随机事件发生的概率.
下面再看两个例子.
从上表中你能发现什么?
1.某农科院所通过抽样试验来估计一大批种子(总体)的发芽率,为此,从中抽取10批,分别做发芽试验.记录下每批发芽粒数,并算出发芽的频率发芽粒数与每批试验粒数之比.结果如下表:
由上面试验所得数据可以看出:当发芽试验样本容量增大时,发芽的频率逐渐稳定到常数0.9.
2.某乒乓球生产厂,从最近生产的一大批乒乓球中抽取6批进行质量检测,结果如下表:
由上面检测所得数据可以看出:当质量检测样本容量增大时,优等品的频率逐渐稳定常数到0.95.
从上表中你能发现什么?
由上面两个例子说明,一般随机事件具有一个极为重要的特性——频率的稳定性,即在大次数重复试验中,随机事件发生的频率总是稳定到一个常数.我们就用频率所稳定到的这个常数来衡量该随机事件发生可能性的大小.于是,就认为第1个例子中种子发芽的概率为0.9,第2个例子中乒乓球优等品的概率为0.95.
随机事件及其概率
一般地,在大量重复进行同一试验时,随机事件A发生的频率
(n为实验的次数,m是事件发生的频数)总是接近于某个常数P。于是,我们用P这个常数表示随机事件A发生的概率,记做
这样,求一个随机事件概率的基本方法可以是:通过大量重复试验,用这个随机事件发生的频率作为它的概率的估计值.
某农科所在相同条件下做了某作物种子发芽率的实验,结果如下表所示:
0.94
0.94
0.94
0.96
0.87
0.89
0.89
0.9
0.9
0.98
种子个数
发芽种子个数
发芽种子频率
100
94
200
187
300
282
400
338
500
435
600
530
700
624
800
718
900
814
1000
981
一般地,1
000千克种子中大约有多少是不能发芽的?
解:
这批种子的发芽的频率稳定在0.9即种子发芽的概率为90%,不发芽的概率为0.1,机不发芽率为10%.
所以:
1000×10%=100千克
答:1000千克种子大约有100千克是不能发芽的.
某射手进行射击,结果如下表所示:
填表:
(1)这个射手射击一次,击中靶心的概率是多少?
0.5
(2)这射手射击1600次,击中靶心的次数是 。
800
0.65
0.58
0.52
0.51
0.55
射击次数n
20
100
200
500
800
击中靶心次数m
13
58
104
255
404
击中靶心频率m/n
本节课我们学习了什么知识?你有哪些收获?还有什么疑惑吗?
必做题:书本P109第1,2,3题
选做题:书本P109数学园地
现实是此岸,成功是彼岸,中间隔着湍急的河流,兴趣便是河上的桥,只要行动就可以通过.
—克雷洛夫
