一元二次方程的应用
图片预览






文档简介
(共14张PPT)
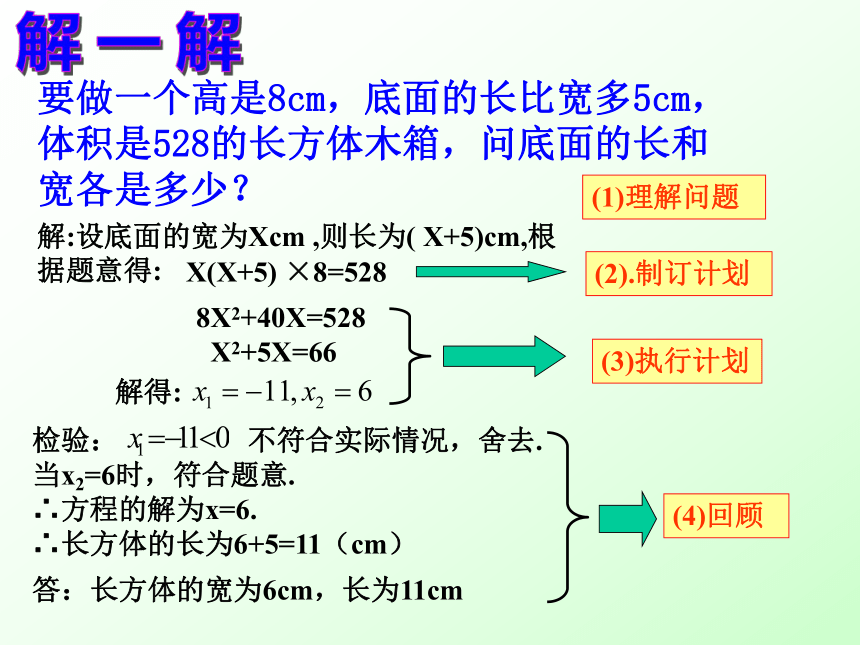
要做一个高是8cm,底面的长比宽多5cm,体积是528的长方体木箱,问底面的长和宽各是多少?
解:设底面的宽为Xcm ,则长为( X+5)cm,根据题意得:
(2).制订计划
(1)理解问题
X(X+5) ×8=528
8X2+40X=528
X2+5X=66
解得:
检验: 不符合实际情况,舍去.当x2=6时,符合题意.
∴方程的解为x=6.
∴长方体的长为6+5=11(cm)
答:长方体的宽为6cm,长为11cm
(3)执行计划
(4)回顾
列方程解应用题的基本步骤:
①理解问题
②制订计划
③执行计划
④回顾
------设
------列
------解
------检
------答
已知两个连续正奇数的积等于63,求这两个数.
经检验,x1=7,x2=-9,是方程的解,但x2=-9
不合题意,舍去
1.某花圃用花盆培育某种花苗,经过实验发现每
盆的盈利与每盆的株数构成一定的关系.每盆植
入3株时,平均单株盈利3元;以同样的栽培条件,
若每盆每增加1株,平均单株盈利就减少0.5元.要
使每盆的盈利达到10元,每盆应该植多少株
分析: 本题涉及的主要数量有每盆的花苗株数,平均单株盈利,每盆花苗的盈利.
主要数量关系有:
平均单株盈利×株数=每盆盈利;
平均单株盈利=3-0.5×每盆增加的株数.
化简,整理,得 x2-3x+2=0
解这个方程,得 x1=1,x2=2.
经检验,x1=1,x2=2都是方程的解,且符合题意.
答:要使每盆的盈利达到10元,每盆应植入4株或5株.
解:设每盆花苗增加x株,则每盆花苗有(3+x)株,平均单株盈利为(3-0.5x)元.由题意得:
(x+3) (3-0.5x)=10
例1。某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮传播就回有81台被感染,请用你学过的知识分析,每轮感染中一台电脑平均感染几台电脑?若病毒得不到有效控制,3轮感染后被感染的电脑会不会超过700台?
例2。某校八年级举行一场篮球友谊赛,赛制为单循环形式,共有28场比赛,问八年级有多少个班?
1.由于自然灾害和认为破坏等因素,某地山林面积连续两年减少,现在的面积比原来减少了36%。问:平均每年减少百分之几。
2.我省农作物秸秆资源巨大,但合理利用量十分有限,2008年的利用率之忧30%,假定我省每年农作物秸秆总量不变,且合理利用量的增长率相同,要使2010年的利用率提高到60%,求每年的增长率。
1.某试验田去年亩产1000斤,今年比去年增产10%,则今年亩产为___________斤,计划明年再增产10%,则明年的产量为 斤。
2.某厂一月份产钢50吨,二、三月份的增长率都是x,则该厂三月分产钢______________吨.
1100
1210
50(1+x)2
增长问题的数量关系是:
一次增长:新数 = 基数×(1+增长率)
二次增长:新数 = 基数×(1+增长率)2
n次增长:新数 = 基数×(1+增长率)n
1.学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册.求这两年的年平均增长率.
2.某公司一月份的营业额为100万元,第一季度总营业额为331万元,求二、三月份平均每月的增长率是多少?
3.某种药剂原售价为4元, 经过两次降价, 现
在每瓶售价为2.56元,问平均每次降价百分
之几
5.某公司计划经过两年把某种商品的生产成本降低19%,那么平均每年需降低百分之几
4.某校坚持对学生进行近视眼的防治,据统计今年的近视学生人数是前年近视学生的75%,那么这两年平均每年近视学生人数降低的百分率是多少
要做一个高是8cm,底面的长比宽多5cm,体积是528的长方体木箱,问底面的长和宽各是多少?
解:设底面的宽为Xcm ,则长为( X+5)cm,根据题意得:
(2).制订计划
(1)理解问题
X(X+5) ×8=528
8X2+40X=528
X2+5X=66
解得:
检验: 不符合实际情况,舍去.当x2=6时,符合题意.
∴方程的解为x=6.
∴长方体的长为6+5=11(cm)
答:长方体的宽为6cm,长为11cm
(3)执行计划
(4)回顾
列方程解应用题的基本步骤:
①理解问题
②制订计划
③执行计划
④回顾
------设
------列
------解
------检
------答
已知两个连续正奇数的积等于63,求这两个数.
经检验,x1=7,x2=-9,是方程的解,但x2=-9
不合题意,舍去
1.某花圃用花盆培育某种花苗,经过实验发现每
盆的盈利与每盆的株数构成一定的关系.每盆植
入3株时,平均单株盈利3元;以同样的栽培条件,
若每盆每增加1株,平均单株盈利就减少0.5元.要
使每盆的盈利达到10元,每盆应该植多少株
分析: 本题涉及的主要数量有每盆的花苗株数,平均单株盈利,每盆花苗的盈利.
主要数量关系有:
平均单株盈利×株数=每盆盈利;
平均单株盈利=3-0.5×每盆增加的株数.
化简,整理,得 x2-3x+2=0
解这个方程,得 x1=1,x2=2.
经检验,x1=1,x2=2都是方程的解,且符合题意.
答:要使每盆的盈利达到10元,每盆应植入4株或5株.
解:设每盆花苗增加x株,则每盆花苗有(3+x)株,平均单株盈利为(3-0.5x)元.由题意得:
(x+3) (3-0.5x)=10
例1。某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮传播就回有81台被感染,请用你学过的知识分析,每轮感染中一台电脑平均感染几台电脑?若病毒得不到有效控制,3轮感染后被感染的电脑会不会超过700台?
例2。某校八年级举行一场篮球友谊赛,赛制为单循环形式,共有28场比赛,问八年级有多少个班?
1.由于自然灾害和认为破坏等因素,某地山林面积连续两年减少,现在的面积比原来减少了36%。问:平均每年减少百分之几。
2.我省农作物秸秆资源巨大,但合理利用量十分有限,2008年的利用率之忧30%,假定我省每年农作物秸秆总量不变,且合理利用量的增长率相同,要使2010年的利用率提高到60%,求每年的增长率。
1.某试验田去年亩产1000斤,今年比去年增产10%,则今年亩产为___________斤,计划明年再增产10%,则明年的产量为 斤。
2.某厂一月份产钢50吨,二、三月份的增长率都是x,则该厂三月分产钢______________吨.
1100
1210
50(1+x)2
增长问题的数量关系是:
一次增长:新数 = 基数×(1+增长率)
二次增长:新数 = 基数×(1+增长率)2
n次增长:新数 = 基数×(1+增长率)n
1.学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册.求这两年的年平均增长率.
2.某公司一月份的营业额为100万元,第一季度总营业额为331万元,求二、三月份平均每月的增长率是多少?
3.某种药剂原售价为4元, 经过两次降价, 现
在每瓶售价为2.56元,问平均每次降价百分
之几
5.某公司计划经过两年把某种商品的生产成本降低19%,那么平均每年需降低百分之几
4.某校坚持对学生进行近视眼的防治,据统计今年的近视学生人数是前年近视学生的75%,那么这两年平均每年近视学生人数降低的百分率是多少
