人教版七年级数学下册7.1.1有序数对课件(共37张PPT)
文档属性
| 名称 | 人教版七年级数学下册7.1.1有序数对课件(共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-21 22:02:07 | ||
图片预览











文档简介
(共37张PPT)
初一年级
数学
有序数对
第七章
平面直角坐标系
本章介绍
(一)有序数对
(二)平面直角坐标系
(三)用坐标表示地理位置
(四)用坐标表示平移
情境引入
问题1 我校运动会开幕式上,几百名学生组成了美丽的图案,用流动的艺术表达了对母校的热爱.你知道它是怎么组成的吗?
情境引入
参加图案表演的每个人都根据图案设计的要求,按排号、列号站在一个确定的位置,随着指挥员的信号,举起自己的道具,整个方阵就组成了美丽的图案.
情境引入
问题2 同学们去影剧院看电影时,你怎么找到自己的座位?
情境引入
问题3 你若发现一本书某页有一处印刷错误,怎样告诉其他同学这一处的位置?
只要说明该页上“第几行”和“第几个字”,同学就可以快速找到错误的位置了.
情境引入
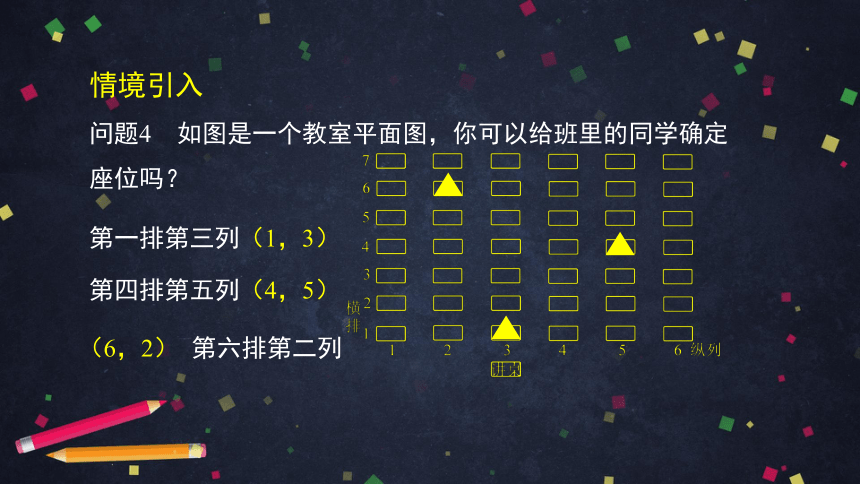
问题4 如图是一个教室平面图,你可以给班里的同学确定座位吗?
第一排第三列(1,3)
第四排第五列(4,5)
(6,2)
第六排第二列
探究新知
如果某同学坐在第a排第b列,应该怎么表示呢?
第a排第b列(a
,b)
探究新知
我们把这种有顺序的两个数a与b组成的数对,
叫做有序数对,记作(
a
,b
).
探究新知
在平面内,利用有序数对,可以准确地表示出一个位置,也就是能用有序数对表示位置.
生活中还有很多例子,你能再举出一些吗?
?
?
?
?
典型例题
例1
(1)如图,甲处表示2街与4巷的十字路口,乙处表示4街与2巷的十字路口.如果用(2,4)
表示甲处的位置,那么
“(2,4)
(2,3)
(2,2)
(3,2)
(4,2)”表示从
甲处到乙处的一种路线.
请你用
这种形式写出一种从甲处到乙处的路线.
5巷
4巷
3巷
2巷
1巷
1街
2街
3街
4街
5街
甲
乙
?
?
?
?
典型例题
例1
(1)法1
解:从甲(2,4)到乙(4,2),路线如图所示.
5巷
4巷
3巷
2巷
1巷
1街
2街
3街
4街
5街
甲
乙
(2,4)
(3,4)
(4,4)
(4,3)
(4,2)..
?
?
?
?
典型例题
例1
(1)法2
解:从甲(2,4)到乙(4,2),路线如图所示.
5巷
4巷
3巷
2巷
1巷
1街
2街
3街
4街
5街
甲
乙
(2,4)
(2,3)
(3,3)
(3,2)
(4,2).
?
?
?
?
典型例题
例1
(2)如果某同学从4街3巷(4,3)出发,按如下路线行走:
“(4,3)
(4,4)
(5,4)
(5,3),”你能
在图中画出他走的路线吗?
5巷
4巷
3巷
2巷
1巷
1街
2街
3街
4街
5街
?
?
?
?
典型例题
例1
(2)如果某同学从4街3巷(4,3)出发,按如下路线行走:
“(4,3)
(4,4)
(5,4)
(5,3),”你能
在图中画出他走的路线吗?
5巷
4巷
3巷
2巷
1巷
1街
2街
3街
4街
5街
解:路线如图所示.
典型例题
例2
如图,象棋棋盘上马所处的位置为(2,3),
(1)象的位置是
;
(2)马走“日”,则它
下一步可以到达的位置
有哪些?
(5,3
)
?
?
?
?
?
?
?
?
9
8
7
6
5
4
3
2
1
5
4
3
2
1
典型例题
例2
(2)解:马走“日”,则它下一步可以到达以下位置:
?
?
?
?
?
?
?
?
9
8
7
6
5
4
3
2
1
5
4
3
2
1
(1,1),(1,5),
(3,1),(3,5),
(4,2),(4,4).
典型例题
例3
如图是雷达探测到的六个目标,若目标C用(6,120°)表示,目标F用(5,210°)表示,
请表示出其余各目标.
解:A(5
,30°)
B(2
,90°)
D(4
,240°)
E(3
,300°)
A
B
C
E
D
F
典型例题
例4
图中显示了10名学生平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时).
(1)
用有序数对表示图中各点.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
5
5
典型例题
(1)解:各点坐标分别是(1,6),(1,9),(2,7),(3,5),(4,2),(5,5),(6,4),(7,2),(7,3),(9,1);
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
0
1
2
3
4
5
6
7
8
9
10
109
8
7
6
5
4
3
2
1
典型例题
例4
(2)
图中有一个点位于方格的对角线上,这表示什么意思?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
0
1
2
3
4
5
6
7
8
9
10
109
8
7
6
5
4
3
2
1
典型例题
(2)
解:图中对角线上这个点表示这位同学每周用于阅读课外书的时间和用于看电视的时间相同;
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
0
1
2
3
4
5
6
7
8
9
10
109
8
7
6
5
4
3
2
1
(5,5)
典型例题
例4
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
0
1
2
3
4
5
6
7
8
9
10
109
8
7
6
5
4
3
2
1
典型例题
(3)
解:对角线左上方的点表示每周阅读课外书的时间比每周看电视的时间多,对角线右下方的点表示每周阅读课外书的时间比每周看电视的时间少;
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
0
1
2
3
4
5
6
7
8
9
10
109
8
7
6
5
4
3
2
1
(1,6)
(1,9)
(2,7)
(3,5)
(4,2)
(6,4)
(7,2)
(7,3)
(9,1)
典型例题
例4
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
0
1
2
3
4
5
6
7
8
9
10
109
8
7
6
5
4
3
2
1
巩固练习
1.
根据下列表述,能确定一个点的位置的是(
)
A.
北纬39.9°,东经116.4°
B.
东城区平安大街
C.
北偏东60°
D.
电影院5排
A
巩固练习
2.
小丽家、小华家、小明家的位置如图所示,如果小丽家的位置用(0,0)表示,小华家的位置用(3,1)表示,那么小明家的位置可以表示成(
)
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
小丽家
小华家
小明家
0
1
2
3
4
5
5
4
3
2
1
A.(4,2)
B.(2,5)
C.(2,4)
D.(3,4)
C
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
巩固练习
3.
如图,已知点O
(0,0),点B
(1,2),
(1)如果点A在线段OM上,三角形OAB的面积为2,那么点A的位置用有序数对可以
表示为
;
O
M
N
B
5
4
3
2
1
0
1
2
3
4
5
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
巩固练习
3.
如图,已知点O
(0,0),点B
(1,2),
(1)如果点A在线段OM上,三角形OAB的面积为2,那么点A的位置用有序数对可以
表示为
;
O
M
N
B
5
4
3
2
1
0
1
2
3
4
5
A
(2,0)
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
巩固练习
3.
如图,已知点O
(0,0),点B
(1,2),
(2)如果点A在线段ON上,三角形OAB的面积为2,那么点A的位置用有序数对可以
表示为
.
O
M
N
B
5
4
3
2
1
0
1
2
3
4
5
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
巩固练习
3.
如图,已知点O
(0,0),点B
(1,2),
(2)如果点A在线段ON上,三角形OAB的面积为2,那么点A的位置用有序数对可以
表示为
.
O
M
N
B
5
4
3
2
1
0
1
2
3
4
5
(0,4)
A
归纳小结
1.
我们把这种有顺序的两个数a与b组成的数对,叫做有序数对,记作(
a
,b
);
2.“有序数对”中的“有序”不能省略;
3.
有序数对可以表示平面内一个点的位置.
课后作业
1.
如图,甲处表示2街与5巷的十字路口,乙处表示5街与2巷的十字路口.如果用(2,5)表示甲处的位置,那么“(2,5)
(3,5)
(4,5)
(5,5)
(5,4)
(5,3)
(5,2)”表示从甲处到乙处的一种路线.
请你用这种形式写出几种从甲处到乙处的路线.
?
?
?
?
?
?
?
?
?
?
6巷
5巷
4巷
3巷
2巷
1巷
1街
2街
3街
4街
5街
6街
甲
乙
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
课后作业
2.
如图,写出表示
下列各点的有序数对:
A(
,
);B(5,2)
;
C(
,
);D(
,
);
E(
,
);F(
,
);
G(
,
);H(
,
);
I
(
,
).
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10
11
A
B
C
D
E
F
G
H
I
祝同学们学习进步!
数学史介绍
法国数学家笛卡尔
数学史介绍
笛卡尔的设想将几何问题数量化,由此诞生了一门新的数学分支——解析几何.这好像是在被一条大河隔开的代数和几何的两岸,架起了一座桥梁,把“数”与“形”联系起来,引起了数学的深刻革命.
初一年级
数学
有序数对
第七章
平面直角坐标系
本章介绍
(一)有序数对
(二)平面直角坐标系
(三)用坐标表示地理位置
(四)用坐标表示平移
情境引入
问题1 我校运动会开幕式上,几百名学生组成了美丽的图案,用流动的艺术表达了对母校的热爱.你知道它是怎么组成的吗?
情境引入
参加图案表演的每个人都根据图案设计的要求,按排号、列号站在一个确定的位置,随着指挥员的信号,举起自己的道具,整个方阵就组成了美丽的图案.
情境引入
问题2 同学们去影剧院看电影时,你怎么找到自己的座位?
情境引入
问题3 你若发现一本书某页有一处印刷错误,怎样告诉其他同学这一处的位置?
只要说明该页上“第几行”和“第几个字”,同学就可以快速找到错误的位置了.
情境引入
问题4 如图是一个教室平面图,你可以给班里的同学确定座位吗?
第一排第三列(1,3)
第四排第五列(4,5)
(6,2)
第六排第二列
探究新知
如果某同学坐在第a排第b列,应该怎么表示呢?
第a排第b列(a
,b)
探究新知
我们把这种有顺序的两个数a与b组成的数对,
叫做有序数对,记作(
a
,b
).
探究新知
在平面内,利用有序数对,可以准确地表示出一个位置,也就是能用有序数对表示位置.
生活中还有很多例子,你能再举出一些吗?
?
?
?
?
典型例题
例1
(1)如图,甲处表示2街与4巷的十字路口,乙处表示4街与2巷的十字路口.如果用(2,4)
表示甲处的位置,那么
“(2,4)
(2,3)
(2,2)
(3,2)
(4,2)”表示从
甲处到乙处的一种路线.
请你用
这种形式写出一种从甲处到乙处的路线.
5巷
4巷
3巷
2巷
1巷
1街
2街
3街
4街
5街
甲
乙
?
?
?
?
典型例题
例1
(1)法1
解:从甲(2,4)到乙(4,2),路线如图所示.
5巷
4巷
3巷
2巷
1巷
1街
2街
3街
4街
5街
甲
乙
(2,4)
(3,4)
(4,4)
(4,3)
(4,2)..
?
?
?
?
典型例题
例1
(1)法2
解:从甲(2,4)到乙(4,2),路线如图所示.
5巷
4巷
3巷
2巷
1巷
1街
2街
3街
4街
5街
甲
乙
(2,4)
(2,3)
(3,3)
(3,2)
(4,2).
?
?
?
?
典型例题
例1
(2)如果某同学从4街3巷(4,3)出发,按如下路线行走:
“(4,3)
(4,4)
(5,4)
(5,3),”你能
在图中画出他走的路线吗?
5巷
4巷
3巷
2巷
1巷
1街
2街
3街
4街
5街
?
?
?
?
典型例题
例1
(2)如果某同学从4街3巷(4,3)出发,按如下路线行走:
“(4,3)
(4,4)
(5,4)
(5,3),”你能
在图中画出他走的路线吗?
5巷
4巷
3巷
2巷
1巷
1街
2街
3街
4街
5街
解:路线如图所示.
典型例题
例2
如图,象棋棋盘上马所处的位置为(2,3),
(1)象的位置是
;
(2)马走“日”,则它
下一步可以到达的位置
有哪些?
(5,3
)
?
?
?
?
?
?
?
?
9
8
7
6
5
4
3
2
1
5
4
3
2
1
典型例题
例2
(2)解:马走“日”,则它下一步可以到达以下位置:
?
?
?
?
?
?
?
?
9
8
7
6
5
4
3
2
1
5
4
3
2
1
(1,1),(1,5),
(3,1),(3,5),
(4,2),(4,4).
典型例题
例3
如图是雷达探测到的六个目标,若目标C用(6,120°)表示,目标F用(5,210°)表示,
请表示出其余各目标.
解:A(5
,30°)
B(2
,90°)
D(4
,240°)
E(3
,300°)
A
B
C
E
D
F
典型例题
例4
图中显示了10名学生平均每周用于阅读课外书的时间和用于看电视的时间(单位:小时).
(1)
用有序数对表示图中各点.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
5
5
典型例题
(1)解:各点坐标分别是(1,6),(1,9),(2,7),(3,5),(4,2),(5,5),(6,4),(7,2),(7,3),(9,1);
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
0
1
2
3
4
5
6
7
8
9
10
109
8
7
6
5
4
3
2
1
典型例题
例4
(2)
图中有一个点位于方格的对角线上,这表示什么意思?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
0
1
2
3
4
5
6
7
8
9
10
109
8
7
6
5
4
3
2
1
典型例题
(2)
解:图中对角线上这个点表示这位同学每周用于阅读课外书的时间和用于看电视的时间相同;
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
0
1
2
3
4
5
6
7
8
9
10
109
8
7
6
5
4
3
2
1
(5,5)
典型例题
例4
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
0
1
2
3
4
5
6
7
8
9
10
109
8
7
6
5
4
3
2
1
典型例题
(3)
解:对角线左上方的点表示每周阅读课外书的时间比每周看电视的时间多,对角线右下方的点表示每周阅读课外书的时间比每周看电视的时间少;
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
0
1
2
3
4
5
6
7
8
9
10
109
8
7
6
5
4
3
2
1
(1,6)
(1,9)
(2,7)
(3,5)
(4,2)
(6,4)
(7,2)
(7,3)
(9,1)
典型例题
例4
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
用于阅读的时间
用于看电视的时间
0
1
2
3
4
5
6
7
8
9
10
109
8
7
6
5
4
3
2
1
巩固练习
1.
根据下列表述,能确定一个点的位置的是(
)
A.
北纬39.9°,东经116.4°
B.
东城区平安大街
C.
北偏东60°
D.
电影院5排
A
巩固练习
2.
小丽家、小华家、小明家的位置如图所示,如果小丽家的位置用(0,0)表示,小华家的位置用(3,1)表示,那么小明家的位置可以表示成(
)
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
小丽家
小华家
小明家
0
1
2
3
4
5
5
4
3
2
1
A.(4,2)
B.(2,5)
C.(2,4)
D.(3,4)
C
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
巩固练习
3.
如图,已知点O
(0,0),点B
(1,2),
(1)如果点A在线段OM上,三角形OAB的面积为2,那么点A的位置用有序数对可以
表示为
;
O
M
N
B
5
4
3
2
1
0
1
2
3
4
5
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
巩固练习
3.
如图,已知点O
(0,0),点B
(1,2),
(1)如果点A在线段OM上,三角形OAB的面积为2,那么点A的位置用有序数对可以
表示为
;
O
M
N
B
5
4
3
2
1
0
1
2
3
4
5
A
(2,0)
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
巩固练习
3.
如图,已知点O
(0,0),点B
(1,2),
(2)如果点A在线段ON上,三角形OAB的面积为2,那么点A的位置用有序数对可以
表示为
.
O
M
N
B
5
4
3
2
1
0
1
2
3
4
5
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
巩固练习
3.
如图,已知点O
(0,0),点B
(1,2),
(2)如果点A在线段ON上,三角形OAB的面积为2,那么点A的位置用有序数对可以
表示为
.
O
M
N
B
5
4
3
2
1
0
1
2
3
4
5
(0,4)
A
归纳小结
1.
我们把这种有顺序的两个数a与b组成的数对,叫做有序数对,记作(
a
,b
);
2.“有序数对”中的“有序”不能省略;
3.
有序数对可以表示平面内一个点的位置.
课后作业
1.
如图,甲处表示2街与5巷的十字路口,乙处表示5街与2巷的十字路口.如果用(2,5)表示甲处的位置,那么“(2,5)
(3,5)
(4,5)
(5,5)
(5,4)
(5,3)
(5,2)”表示从甲处到乙处的一种路线.
请你用这种形式写出几种从甲处到乙处的路线.
?
?
?
?
?
?
?
?
?
?
6巷
5巷
4巷
3巷
2巷
1巷
1街
2街
3街
4街
5街
6街
甲
乙
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
课后作业
2.
如图,写出表示
下列各点的有序数对:
A(
,
);B(5,2)
;
C(
,
);D(
,
);
E(
,
);F(
,
);
G(
,
);H(
,
);
I
(
,
).
9
8
7
6
5
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10
11
A
B
C
D
E
F
G
H
I
祝同学们学习进步!
数学史介绍
法国数学家笛卡尔
数学史介绍
笛卡尔的设想将几何问题数量化,由此诞生了一门新的数学分支——解析几何.这好像是在被一条大河隔开的代数和几何的两岸,架起了一座桥梁,把“数”与“形”联系起来,引起了数学的深刻革命.
