人教版数学七年级上册4.3.2角的比较与运算(1)课件(22张PPT)
文档属性
| 名称 | 人教版数学七年级上册4.3.2角的比较与运算(1)课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 361.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 16:48:19 | ||
图片预览






文档简介
(共22张PPT)
4.3.2角的比较与运算
几何图形初步
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
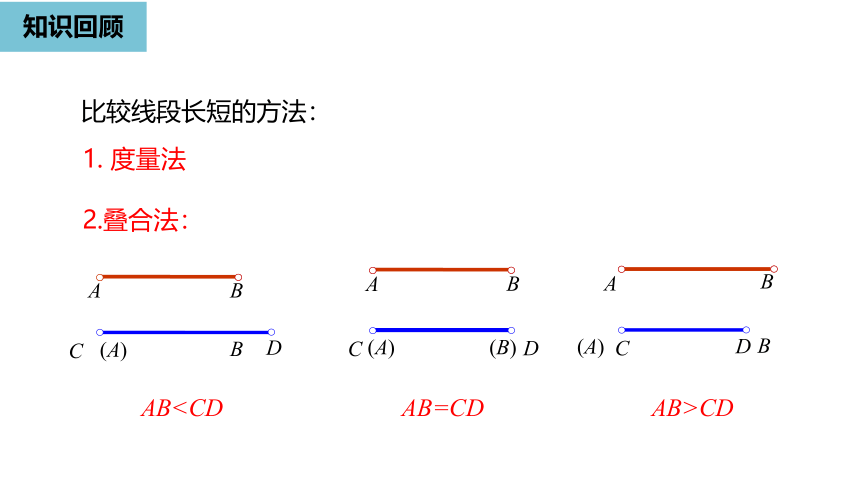
AB>CD
ABAB=CD
比较线段长短的方法:
1.
度量法
2.叠合法:
(A)
B
B
A
C
D
C
D
A
B
(A)
(B)
C
D
B
(A)
B
A
学习目标
1.
掌握角的大小的比较方法.
2.
理解角平分线和角的和、差、倍、分的意义及数量关系,能够用几何语言进行相关表述,并能解答相关问题.
课堂导入
有一天学生张亮和王帅各带了一把折扇(如图所示),下面是他们的一段对话:
张:我的折扇张开大一些,所以我的折扇的角也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
知识点1
新知探究
同学们,你们有办法帮他们进行判断吗?
A
B
C
D
E
F
怎样比较∠ABC和∠DEF
的大小?
知识点1
新知探究
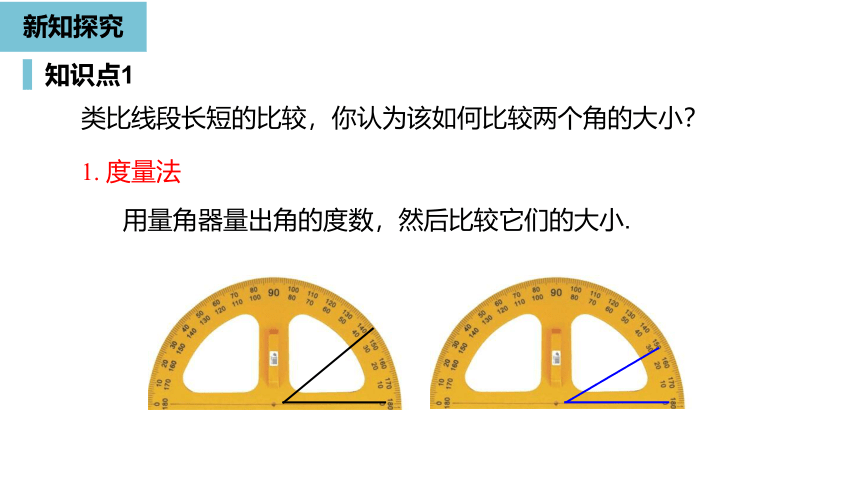
类比线段长短的比较,你认为该如何比较两个角的大小?
1.
度量法
用量角器量出角的度数,然后比较它们的大小.
知识点1
新知探究
A
B
O
(O'
)
B'
(A'
)
A
B
O
A
B
O
(O'
)
B'
(A'
)
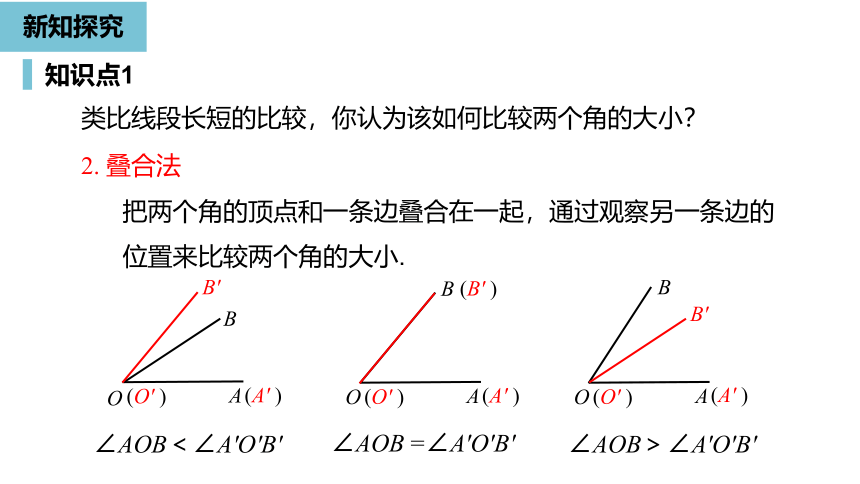
∠AOB<∠A'O'B'
∠AOB
=∠A'O'B'
∠AOB>∠A'O'B'
(O'
)
(B'
)
(A'
)
类比线段长短的比较,你认为该如何比较两个角的大小?
2.
叠合法
把两个角的顶点和一条边叠合在一起,通过观察另一条边的位置来比较两个角的大小.
知识点1
新知探究
使用叠合法比较角的大小的关键点:
①
重合,即顶点重合,一条边重合;
②
同侧,即另一条边放在重合边的同一侧.
知识点1
新知探究
1.
角的大小关系和角的度数的大小关系是一致的.从数量方面进行比较,度数大的角也大;从形状上看,开口大的角也大.
2.
比较角的大小有时也可用估测法:直接通过观察,比较角的大小.此方法较为直观,但不够精准,仅适用于角度差别较大或精确度要求不高的角的大小的比较.
跟踪训练
新知探究
如图所示,回答下列问题:
(1)
比较∠FOD
与∠BOD
的大小;
(2)
比较∠AOD与∠BOD
的大小;
(3)
借助量角器比较∠AOE
与∠DOF的大小.
解:(1)
∠FOD
<
∠BOD
.
(2)
∠AOD
>
∠BOD
.
(3)
∠AOE
=
∠DOF
.
知识点2
新知探究
图中有几个角?它们之间有什么关系?
图中有3个角:∠AOC,∠AOB,∠BOC.
∠AOC
是∠AOB
与∠BOC的和,记作∠AOC
=
∠AOB
+∠BOC;
它们的关系:
∠AOB
是∠AOC与∠BOC的差,记作∠AOB
=
∠AOC-∠BOC;
类似地,∠AOC-∠AOB=∠BOC.
A
B
O
C
根据右图回答下列问题:
(1)
∠AOC
是哪两个角的和?∠BOD
是哪两个角的和?
(2)
∠AOB是哪两个角的差?
跟踪训练
新知探究
B
A
O
C
D
解:(1)
∠AOC
=∠AOB
+∠BOC,∠BOD=∠BOC+∠COD.
(2)
∠AOB
=∠AOC
-∠BOC
=∠AOD-∠BOD.
知识点3
新知探究
B
A
O
C
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
知识点3
新知探究
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
O
B
A
C
因为
OC
是∠AOB
的角平分线,
所以
∠AOC=∠BOC=
∠AOB,
∠AOB=2∠BOC=2∠AOC.
角的平分线是以这个角的顶点为端点的一条射线.
知识点3
新知探究
角平分线的判定方法
当
OD
在∠AOB
的内部且满足下列情况之一时,就可以判定
OD
是∠AOB的平分线:
①
∠AOD=∠BOD;
②
∠AOD=
∠AOB;
③
∠BOD=
∠AOB;
④
∠AOB=2∠AOD;
⑤
∠AOB=2∠BOD.
知识点3
新知探究
类似地,还有角的三等分线等.
应用格式:
O
B
A
C
因为
OB,OC
是∠AOD
的三等分线,
所以∠AOB=∠BOC
=∠COD=
∠AOD,
∠AOD=3∠AOB=3∠BOC
=3∠COD.
D
跟踪训练
新知探究
射线
OC
在∠AOB的内部,下列给出的条件不能得出
OC
是∠AOB的平分线的是(
)
A.
∠AOC=∠BOC
B.
∠AOC+∠BOC=∠AOB
C.
∠AOB=2∠AOC
D.
∠BOC=
∠AOB
B
随堂练习
1
比较两个角的大小关系:
小明用度量法测得∠AOB=45°,∠COD=50°;
小丽用叠合法比较,将两个角的顶点重合,边
OB
与
OD
重合,边
OA
和OC
置于重合边的同侧,则边
OA
.(填序号)
①“在∠COD
的内部”;
②“在∠COD
的外部”;
③“与边
OC
重合”.
①
如图,∠l=∠2,∠3=∠4,则下列结论:
①
AD
平分∠BAF;②
AF
平分∠DAC;
③
AE
平分∠DAF;④
AF
平分∠BAC;
⑤
AE
平分∠BAC.
其中,正确的是(
)
A.
①③
B.
③⑤
C.
②④
D.
③④
随堂练习
2
解析:因为∠1
=∠2,所以
AE
平分∠DAF,所以③正确;因为∠l
=∠2,∠3=
∠4,所以∠1
+∠3=∠2
+∠4,即∠BAE=∠CAE,所以
AE
平分∠BAC,所以⑤正确.
B
如图,点
O
为直线
AB
上一点,∠COD=90°
,OE
平分∠AOD.有下列四种结论:①∠AOE=∠EOD,②∠AOC=
∠EOD,③∠AOC+∠BOD=90°,④∠BOD=2∠COE.其中一定正确的个数有(
)
A.4个
B.3个
C.2个
D.1个
随堂练习
3
B
课堂小结
角的比较
度量法
叠合法
角的平分线
角的运算
角的和差倍分关系
如图所示,OB,OC
是∠AOD
内的任意两条射线,OM
平分∠AOB,ON
平分∠COD,若∠MON=α,∠BOC=β,求∠AOD
的度数.
拓展提升
1
解:因为∠MON=
α,∠BOC=β,
所以∠MON-∠BOC=∠CON+∠BOM=
α
-
β.
又因为OM
平分∠AOB,ON平分∠COD,
所以∠AOM=∠BOM,∠CON=∠DON.
由题意,得
∠AOD=∠MON+∠DON+∠AOM=∠MON+∠CON+∠BOM=
α
+
α
-
β=2α
-
β.
4.3.2角的比较与运算
几何图形初步
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
AB>CD
AB
比较线段长短的方法:
1.
度量法
2.叠合法:
(A)
B
B
A
C
D
C
D
A
B
(A)
(B)
C
D
B
(A)
B
A
学习目标
1.
掌握角的大小的比较方法.
2.
理解角平分线和角的和、差、倍、分的意义及数量关系,能够用几何语言进行相关表述,并能解答相关问题.
课堂导入
有一天学生张亮和王帅各带了一把折扇(如图所示),下面是他们的一段对话:
张:我的折扇张开大一些,所以我的折扇的角也大一些.
王:我的折扇长一些,所以我的折扇的角也大一些.
知识点1
新知探究
同学们,你们有办法帮他们进行判断吗?
A
B
C
D
E
F
怎样比较∠ABC和∠DEF
的大小?
知识点1
新知探究
类比线段长短的比较,你认为该如何比较两个角的大小?
1.
度量法
用量角器量出角的度数,然后比较它们的大小.
知识点1
新知探究
A
B
O
(O'
)
B'
(A'
)
A
B
O
A
B
O
(O'
)
B'
(A'
)
∠AOB<∠A'O'B'
∠AOB
=∠A'O'B'
∠AOB>∠A'O'B'
(O'
)
(B'
)
(A'
)
类比线段长短的比较,你认为该如何比较两个角的大小?
2.
叠合法
把两个角的顶点和一条边叠合在一起,通过观察另一条边的位置来比较两个角的大小.
知识点1
新知探究
使用叠合法比较角的大小的关键点:
①
重合,即顶点重合,一条边重合;
②
同侧,即另一条边放在重合边的同一侧.
知识点1
新知探究
1.
角的大小关系和角的度数的大小关系是一致的.从数量方面进行比较,度数大的角也大;从形状上看,开口大的角也大.
2.
比较角的大小有时也可用估测法:直接通过观察,比较角的大小.此方法较为直观,但不够精准,仅适用于角度差别较大或精确度要求不高的角的大小的比较.
跟踪训练
新知探究
如图所示,回答下列问题:
(1)
比较∠FOD
与∠BOD
的大小;
(2)
比较∠AOD与∠BOD
的大小;
(3)
借助量角器比较∠AOE
与∠DOF的大小.
解:(1)
∠FOD
<
∠BOD
.
(2)
∠AOD
>
∠BOD
.
(3)
∠AOE
=
∠DOF
.
知识点2
新知探究
图中有几个角?它们之间有什么关系?
图中有3个角:∠AOC,∠AOB,∠BOC.
∠AOC
是∠AOB
与∠BOC的和,记作∠AOC
=
∠AOB
+∠BOC;
它们的关系:
∠AOB
是∠AOC与∠BOC的差,记作∠AOB
=
∠AOC-∠BOC;
类似地,∠AOC-∠AOB=∠BOC.
A
B
O
C
根据右图回答下列问题:
(1)
∠AOC
是哪两个角的和?∠BOD
是哪两个角的和?
(2)
∠AOB是哪两个角的差?
跟踪训练
新知探究
B
A
O
C
D
解:(1)
∠AOC
=∠AOB
+∠BOC,∠BOD=∠BOC+∠COD.
(2)
∠AOB
=∠AOC
-∠BOC
=∠AOD-∠BOD.
知识点3
新知探究
B
A
O
C
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
知识点3
新知探究
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
O
B
A
C
因为
OC
是∠AOB
的角平分线,
所以
∠AOC=∠BOC=
∠AOB,
∠AOB=2∠BOC=2∠AOC.
角的平分线是以这个角的顶点为端点的一条射线.
知识点3
新知探究
角平分线的判定方法
当
OD
在∠AOB
的内部且满足下列情况之一时,就可以判定
OD
是∠AOB的平分线:
①
∠AOD=∠BOD;
②
∠AOD=
∠AOB;
③
∠BOD=
∠AOB;
④
∠AOB=2∠AOD;
⑤
∠AOB=2∠BOD.
知识点3
新知探究
类似地,还有角的三等分线等.
应用格式:
O
B
A
C
因为
OB,OC
是∠AOD
的三等分线,
所以∠AOB=∠BOC
=∠COD=
∠AOD,
∠AOD=3∠AOB=3∠BOC
=3∠COD.
D
跟踪训练
新知探究
射线
OC
在∠AOB的内部,下列给出的条件不能得出
OC
是∠AOB的平分线的是(
)
A.
∠AOC=∠BOC
B.
∠AOC+∠BOC=∠AOB
C.
∠AOB=2∠AOC
D.
∠BOC=
∠AOB
B
随堂练习
1
比较两个角的大小关系:
小明用度量法测得∠AOB=45°,∠COD=50°;
小丽用叠合法比较,将两个角的顶点重合,边
OB
与
OD
重合,边
OA
和OC
置于重合边的同侧,则边
OA
.(填序号)
①“在∠COD
的内部”;
②“在∠COD
的外部”;
③“与边
OC
重合”.
①
如图,∠l=∠2,∠3=∠4,则下列结论:
①
AD
平分∠BAF;②
AF
平分∠DAC;
③
AE
平分∠DAF;④
AF
平分∠BAC;
⑤
AE
平分∠BAC.
其中,正确的是(
)
A.
①③
B.
③⑤
C.
②④
D.
③④
随堂练习
2
解析:因为∠1
=∠2,所以
AE
平分∠DAF,所以③正确;因为∠l
=∠2,∠3=
∠4,所以∠1
+∠3=∠2
+∠4,即∠BAE=∠CAE,所以
AE
平分∠BAC,所以⑤正确.
B
如图,点
O
为直线
AB
上一点,∠COD=90°
,OE
平分∠AOD.有下列四种结论:①∠AOE=∠EOD,②∠AOC=
∠EOD,③∠AOC+∠BOD=90°,④∠BOD=2∠COE.其中一定正确的个数有(
)
A.4个
B.3个
C.2个
D.1个
随堂练习
3
B
课堂小结
角的比较
度量法
叠合法
角的平分线
角的运算
角的和差倍分关系
如图所示,OB,OC
是∠AOD
内的任意两条射线,OM
平分∠AOB,ON
平分∠COD,若∠MON=α,∠BOC=β,求∠AOD
的度数.
拓展提升
1
解:因为∠MON=
α,∠BOC=β,
所以∠MON-∠BOC=∠CON+∠BOM=
α
-
β.
又因为OM
平分∠AOB,ON平分∠COD,
所以∠AOM=∠BOM,∠CON=∠DON.
由题意,得
∠AOD=∠MON+∠DON+∠AOM=∠MON+∠CON+∠BOM=
α
+
α
-
β=2α
-
β.
