人教版数学七年级上册4.3.3余角和补角(1)课件(25张PPT)
文档属性
| 名称 | 人教版数学七年级上册4.3.3余角和补角(1)课件(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 263.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 16:52:57 | ||
图片预览





文档简介
(共25张PPT)
4.3.3余角和补角
几何图形初步
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
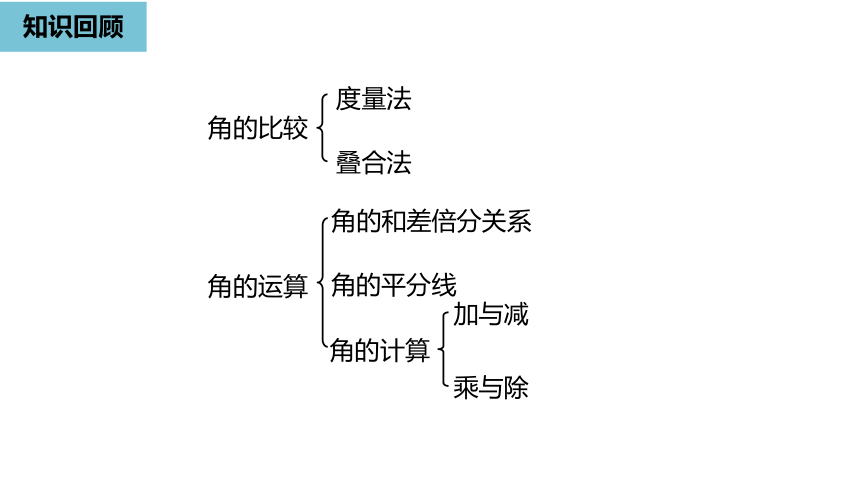
知识回顾
角的比较
度量法
叠合法
角的平分线
角的运算
角的和差倍分关系
加与减
乘与除
角的计算
学习目标
1.
了解余角、补角的概念.
2.
掌握余角和补角的性质,并能利用余角、补角的知识解决相关问题.
课堂导入
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
1.
∠1
与∠2
有什么数量关系?
∠1+∠2
=
90°
2.
∠3与∠4有什么数量关系?
∠3+∠4
=
180°
知识点1
新知探究
1
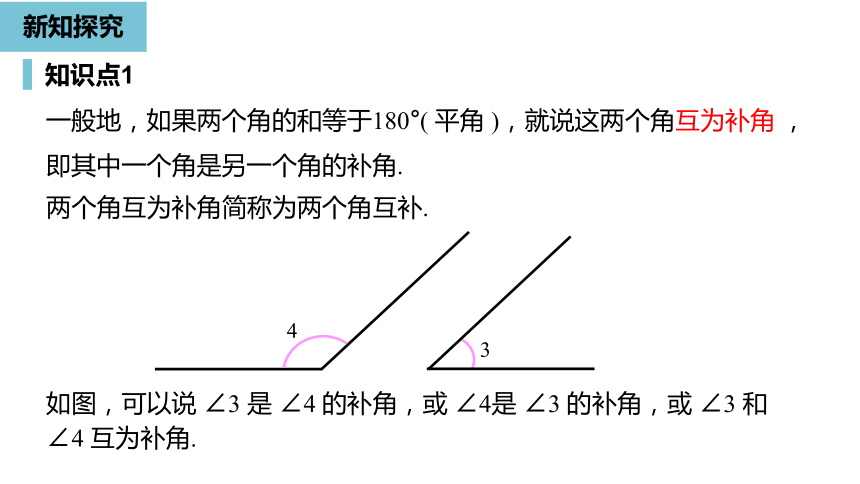
一般地,如果两个角的和等于90°(
直角
),就说这两个角互为余角
,即其中每一个角是另一个角的余角.
如图,可以说
∠1
是
∠2
的余角,或
∠2
是∠1的余角,或
∠1和
∠2互为余角.
2
两个角互为余角简称为两个角互余.
知识点1
新知探究
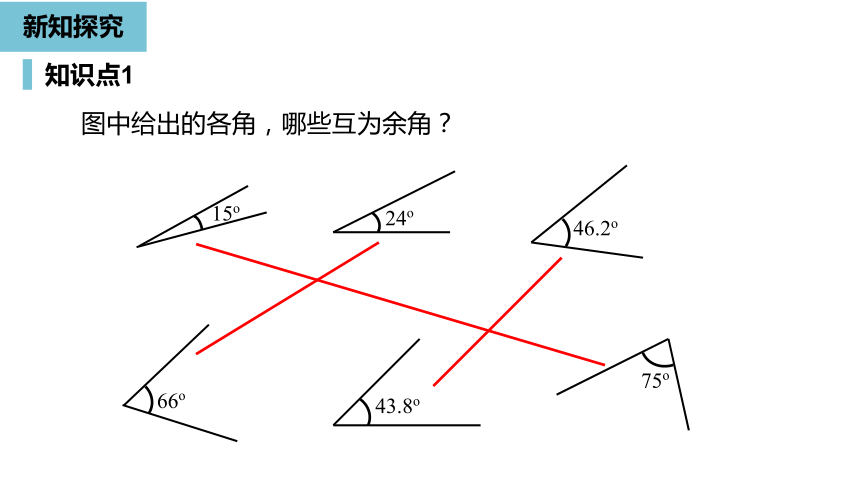
图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
知识点1
新知探究
如图,可以说
∠3
是
∠4
的补角,或
∠4是
∠3
的补角,或
∠3
和
∠4
互为补角.
4
3
一般地,如果两个角的和等于180°(
平角
),就说这两个角互为补角
,即其中一个角是另一个角的补角.
两个角互为补角简称为两个角互补.
知识点1
新知探究
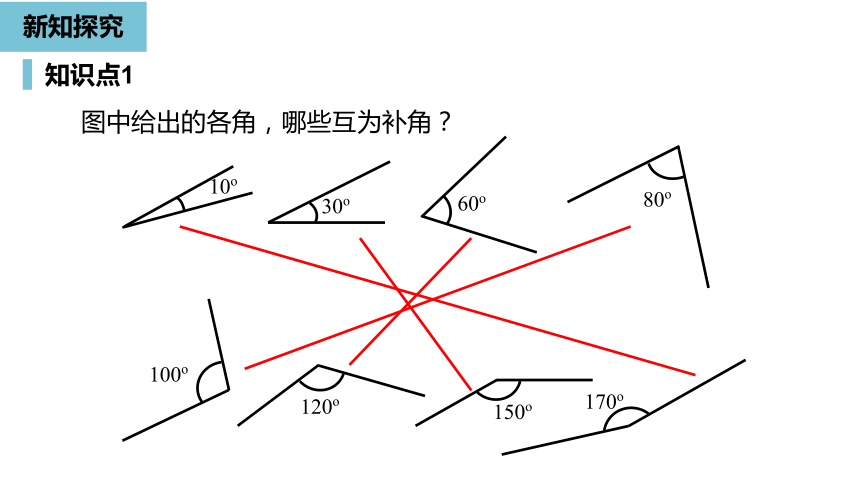
图中给出的各角,哪些互为补角?
10o
30o
60o
80o
120o
150o
170o
100o
知识点1
新知探究
∠α
∠α
的余角
∠α
的补角
5°
32°
45°
77°
62°23′
x°(0<x<90)
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
(90-x)°
(180-x)°
观察可得结论:
锐角的补角比它的余角大_____.
90°
知识点1
新知探究
1.
两个角互余或互补是两个角之间的数量关系,与它们的位置无关,只与角的度数有关.
2.
若两个角互余,则这两个角一定都是锐角;若两个角互补,则这两个角可能都是直角,也可能一个是锐角,另一个是钝角.
跟踪训练
新知探究
(1)
若一个角是20°,则它的余角是
,
它的补角是
;它的补角比它的余角大
.
(2)
若一个角的余角是54°38',则这个角是
,这个角的补角是
.
70°
160°
90°
35°22'
144°38'
知识点2
新知探究
∠1
与∠2,∠3都互为补角,∠2
与∠3
的大小有什么关系?
1
2
同角
(等角)
的补角相等.
3
∠2=180°-∠1
∠3=180°-∠1
∠2
=∠3
知识点2
新知探究
∠1
与∠2,∠3都互为余角,∠2
与∠3
的大小有什么关系?
1
2
同角
(等角)
的余角相等.
3
∠2=90°-∠1
∠3=90°-∠1
∠2
=∠3
知识点2
新知探究
1.
如果互补的两个角相等,那么这两个角都是直角.
2.
“同角”指同一个角,“等角”指度数相等的角.同角一定是等角,但等角不一定是同角.
知识点2
新知探究
例
如图,点A,O,B在同一直线上,射线
OD
和射线
OE
分别平分∠AOC
和∠BOC,图中哪些角互为余角?
解:因为点A,O,B在同一直线上,
所以
∠AOC
和
∠BOC
互为补角.
又因为射线
OD
和射线
OE
分别平分∠AOC
和∠BOC,
所以∠COD+∠COE=
∠AOC+∠BOC
=
(∠AOC+∠BOC
)
=
90°.
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
O
A
B
C
D
E
(1)
如图(1)所示,∠AOB=∠COD=90°,∠1与∠2相等吗?为什么?
跟踪训练
新知探究
解:
(1)
相等.
因为∠COD=90°,所以∠2
+∠BOC
=
90°.
因为∠AOB=90°,所以∠1
+∠BOC=90°.
所以∠1=∠2.
(2)
如图(2)所示,直线
MN
与
PQ
相交于点
E,∠1与∠2相等吗?为什么?
跟踪训练
新知探究
解:(2)
相等.
因为点
M,E,N
在同一条直线上,
所以∠MEN=180°,即∠2+∠PEN=
180°.
因为点
P,E,Q
在同一条直线上,
所以∠PEQ=180°,即∠l
+∠PEN=
180°.
所以∠1=∠2.
随堂练习
1
若一个角为65°,则它的补角的度数为(
)
A.25°
B.35°
C.115°
D.125°
C
解:设这个角的度数是
x.
由题意,得(
180°-x)-3(90°-
x)=10°,
解得
x=50°.
所以这个角是50°.
随堂练习
2
已知一个角的补角比这个角的余角的3倍大10°,这个角是多少度?
如图所示,点
O
为直线
AB
上一点,∠AOC=∠DOE=90°.
(1)
图中互余的角有几对?各是哪些?
随堂练习
3
解:(1)
因为点
O
为直线
AB
上一点,∠AOC=∠DOE
=
90°,
所以∠BOC=180°-∠AOC=180°-90°=90°,
所以∠1+∠2=90°,∠2+∠3=90°,∠3+∠4=90°,∠1+∠4=90°,
所以图中互余的角有4对,
分别是∠1和∠2,∠2和∠3,∠3和∠4,∠1和∠4.
如图所示,点
O
为直线
AB
上一点,∠AOC=∠DOE=90°.
(2)
图中互补的角有几对?各是哪些?
随堂练习
3
解:(2)
由已知得,∠1+∠BOD=180°,∠4+∠AOE=180°,∠AOC+∠BOC=
180°,∠AOC+∠DOE=180°,
由(1)可知,∠1=∠
3,∠2=∠4,∠BOC=90°,
所以∠3+∠BOD=180°
,∠2+∠AOE=
180°,∠BOC+∠DOE=180°.
所以图中互补的角有7对,
分别是∠1和∠BOD,∠4和∠AOE,∠AOC和∠BOC,∠3和∠BOD,∠2和∠AOE,∠AOC和∠DOE,∠BOC
和∠DOE.
互余
互补
两角间的数量关系
对应图形
性质
课堂小结
同角或等角的补角相等
同角或等角的余角相等
一个角的补角与这个角的余角的和比平角少30°,这个角为(
)
A.50°
B.60°
C.90°
D.120°
拓展提升
1
解析:设这个角的度数为
x
,则它的余角为
90°-x,
补角为180°-x,所以(90°-x)
+(180°-x)
+30°=
180°,
解得
x=
60°.
所以这个角为60°.
B
解:因为
A,O,B
三点在同一条直线上,所以∠AOB=
180°.
因为
OD,OE
分别平分∠AOC,∠BOC,
所以∠AOD=∠COD=
∠AOC,∠COE=∠BOE=
∠BOC.
所以∠DOE=∠COD+∠COE=
∠AOC
+
∠BOC
=
(∠AOC+∠BOC)=
∠AOB
=90°.
所以∠AOD+∠COE
=90°,∠AOD+∠BOE=90°.
所以∠AOD的余角为∠COE和∠BOE.
拓展提升
2
如图,OD,OE
分别平分∠AOC,∠BOC,A,O,B
三点在同一条直线上,OF
为
OD
的反向延长线,请分别写出∠AOD
的余角和补角.
解:因为∠COD
+∠COF=∠DOF
=
180°,
所以∠AOD
+∠COF
=
180°.
因为∠AOD
+∠BOD=∠AOB
=
180°,
∠AOD+∠AOF=∠DOF=
180°,
所以∠AOD的补角为∠COF,∠BOD和∠AOF.
拓展提升
2
如图,OD,OE
分别平分∠AOC,∠BOC,A,O,B
三点在同一条直线上,OF
为
OD
的反向延长线,请分别写出∠AOD
的余角和补角.
4.3.3余角和补角
几何图形初步
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
角的比较
度量法
叠合法
角的平分线
角的运算
角的和差倍分关系
加与减
乘与除
角的计算
学习目标
1.
了解余角、补角的概念.
2.
掌握余角和补角的性质,并能利用余角、补角的知识解决相关问题.
课堂导入
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
1.
∠1
与∠2
有什么数量关系?
∠1+∠2
=
90°
2.
∠3与∠4有什么数量关系?
∠3+∠4
=
180°
知识点1
新知探究
1
一般地,如果两个角的和等于90°(
直角
),就说这两个角互为余角
,即其中每一个角是另一个角的余角.
如图,可以说
∠1
是
∠2
的余角,或
∠2
是∠1的余角,或
∠1和
∠2互为余角.
2
两个角互为余角简称为两个角互余.
知识点1
新知探究
图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
知识点1
新知探究
如图,可以说
∠3
是
∠4
的补角,或
∠4是
∠3
的补角,或
∠3
和
∠4
互为补角.
4
3
一般地,如果两个角的和等于180°(
平角
),就说这两个角互为补角
,即其中一个角是另一个角的补角.
两个角互为补角简称为两个角互补.
知识点1
新知探究
图中给出的各角,哪些互为补角?
10o
30o
60o
80o
120o
150o
170o
100o
知识点1
新知探究
∠α
∠α
的余角
∠α
的补角
5°
32°
45°
77°
62°23′
x°(0<x<90)
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
(90-x)°
(180-x)°
观察可得结论:
锐角的补角比它的余角大_____.
90°
知识点1
新知探究
1.
两个角互余或互补是两个角之间的数量关系,与它们的位置无关,只与角的度数有关.
2.
若两个角互余,则这两个角一定都是锐角;若两个角互补,则这两个角可能都是直角,也可能一个是锐角,另一个是钝角.
跟踪训练
新知探究
(1)
若一个角是20°,则它的余角是
,
它的补角是
;它的补角比它的余角大
.
(2)
若一个角的余角是54°38',则这个角是
,这个角的补角是
.
70°
160°
90°
35°22'
144°38'
知识点2
新知探究
∠1
与∠2,∠3都互为补角,∠2
与∠3
的大小有什么关系?
1
2
同角
(等角)
的补角相等.
3
∠2=180°-∠1
∠3=180°-∠1
∠2
=∠3
知识点2
新知探究
∠1
与∠2,∠3都互为余角,∠2
与∠3
的大小有什么关系?
1
2
同角
(等角)
的余角相等.
3
∠2=90°-∠1
∠3=90°-∠1
∠2
=∠3
知识点2
新知探究
1.
如果互补的两个角相等,那么这两个角都是直角.
2.
“同角”指同一个角,“等角”指度数相等的角.同角一定是等角,但等角不一定是同角.
知识点2
新知探究
例
如图,点A,O,B在同一直线上,射线
OD
和射线
OE
分别平分∠AOC
和∠BOC,图中哪些角互为余角?
解:因为点A,O,B在同一直线上,
所以
∠AOC
和
∠BOC
互为补角.
又因为射线
OD
和射线
OE
分别平分∠AOC
和∠BOC,
所以∠COD+∠COE=
∠AOC+∠BOC
=
(∠AOC+∠BOC
)
=
90°.
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
O
A
B
C
D
E
(1)
如图(1)所示,∠AOB=∠COD=90°,∠1与∠2相等吗?为什么?
跟踪训练
新知探究
解:
(1)
相等.
因为∠COD=90°,所以∠2
+∠BOC
=
90°.
因为∠AOB=90°,所以∠1
+∠BOC=90°.
所以∠1=∠2.
(2)
如图(2)所示,直线
MN
与
PQ
相交于点
E,∠1与∠2相等吗?为什么?
跟踪训练
新知探究
解:(2)
相等.
因为点
M,E,N
在同一条直线上,
所以∠MEN=180°,即∠2+∠PEN=
180°.
因为点
P,E,Q
在同一条直线上,
所以∠PEQ=180°,即∠l
+∠PEN=
180°.
所以∠1=∠2.
随堂练习
1
若一个角为65°,则它的补角的度数为(
)
A.25°
B.35°
C.115°
D.125°
C
解:设这个角的度数是
x.
由题意,得(
180°-x)-3(90°-
x)=10°,
解得
x=50°.
所以这个角是50°.
随堂练习
2
已知一个角的补角比这个角的余角的3倍大10°,这个角是多少度?
如图所示,点
O
为直线
AB
上一点,∠AOC=∠DOE=90°.
(1)
图中互余的角有几对?各是哪些?
随堂练习
3
解:(1)
因为点
O
为直线
AB
上一点,∠AOC=∠DOE
=
90°,
所以∠BOC=180°-∠AOC=180°-90°=90°,
所以∠1+∠2=90°,∠2+∠3=90°,∠3+∠4=90°,∠1+∠4=90°,
所以图中互余的角有4对,
分别是∠1和∠2,∠2和∠3,∠3和∠4,∠1和∠4.
如图所示,点
O
为直线
AB
上一点,∠AOC=∠DOE=90°.
(2)
图中互补的角有几对?各是哪些?
随堂练习
3
解:(2)
由已知得,∠1+∠BOD=180°,∠4+∠AOE=180°,∠AOC+∠BOC=
180°,∠AOC+∠DOE=180°,
由(1)可知,∠1=∠
3,∠2=∠4,∠BOC=90°,
所以∠3+∠BOD=180°
,∠2+∠AOE=
180°,∠BOC+∠DOE=180°.
所以图中互补的角有7对,
分别是∠1和∠BOD,∠4和∠AOE,∠AOC和∠BOC,∠3和∠BOD,∠2和∠AOE,∠AOC和∠DOE,∠BOC
和∠DOE.
互余
互补
两角间的数量关系
对应图形
性质
课堂小结
同角或等角的补角相等
同角或等角的余角相等
一个角的补角与这个角的余角的和比平角少30°,这个角为(
)
A.50°
B.60°
C.90°
D.120°
拓展提升
1
解析:设这个角的度数为
x
,则它的余角为
90°-x,
补角为180°-x,所以(90°-x)
+(180°-x)
+30°=
180°,
解得
x=
60°.
所以这个角为60°.
B
解:因为
A,O,B
三点在同一条直线上,所以∠AOB=
180°.
因为
OD,OE
分别平分∠AOC,∠BOC,
所以∠AOD=∠COD=
∠AOC,∠COE=∠BOE=
∠BOC.
所以∠DOE=∠COD+∠COE=
∠AOC
+
∠BOC
=
(∠AOC+∠BOC)=
∠AOB
=90°.
所以∠AOD+∠COE
=90°,∠AOD+∠BOE=90°.
所以∠AOD的余角为∠COE和∠BOE.
拓展提升
2
如图,OD,OE
分别平分∠AOC,∠BOC,A,O,B
三点在同一条直线上,OF
为
OD
的反向延长线,请分别写出∠AOD
的余角和补角.
解:因为∠COD
+∠COF=∠DOF
=
180°,
所以∠AOD
+∠COF
=
180°.
因为∠AOD
+∠BOD=∠AOB
=
180°,
∠AOD+∠AOF=∠DOF=
180°,
所以∠AOD的补角为∠COF,∠BOD和∠AOF.
拓展提升
2
如图,OD,OE
分别平分∠AOC,∠BOC,A,O,B
三点在同一条直线上,OF
为
OD
的反向延长线,请分别写出∠AOD
的余角和补角.
