人教版数学七年级上册4.4课题学习设计制作长方体形状的包装纸盒(2)课件(20张PPT)
文档属性
| 名称 | 人教版数学七年级上册4.4课题学习设计制作长方体形状的包装纸盒(2)课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 318.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 16:54:29 | ||
图片预览






文档简介
(共20张PPT)
4.4 课题学习
设计制作长方体形状的包装纸盒
几何图形初步
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
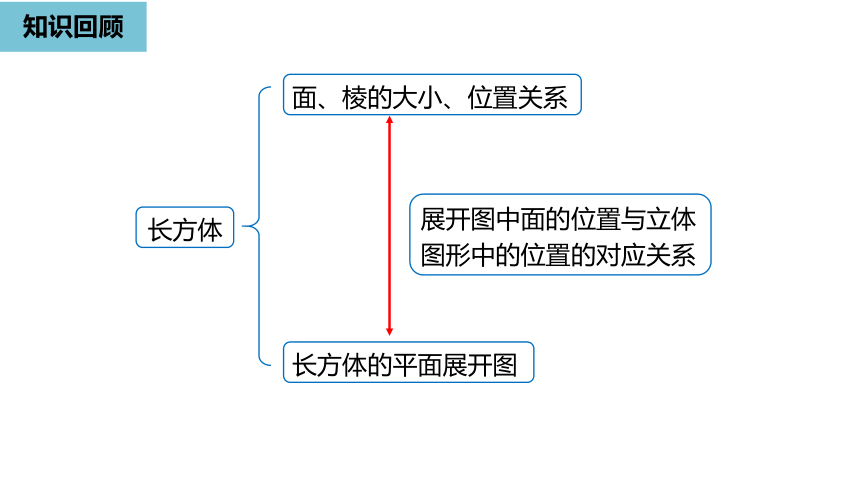
知识回顾
面、棱的大小、位置关系
长方体
长方体的平面展开图
展开图中面的位置与立体图形中的位置的对应关系
学习目标
1.
学生能独立完成包装纸盒的制作.
2.
通过制作过程体会立体图形与平面图形的对应关系.
3.
通过体验观察、思考、操作、总结的过程,增强空间能力.
课堂导入
上节课我们通过动手操作把一个长方体盒子拆开得到它的平面展开图,并尝试进行复原,那么怎么在一张纸上画出长方体的平面展开图并折叠成长方体呢?本节课我们将来解决这个问题.
知识点1
新知探究
要得到如图所示的长方体形状的墨水盒,设计方案内容包括:包装盒的形状、尺寸、外表图案等.
知识点1
新知探究
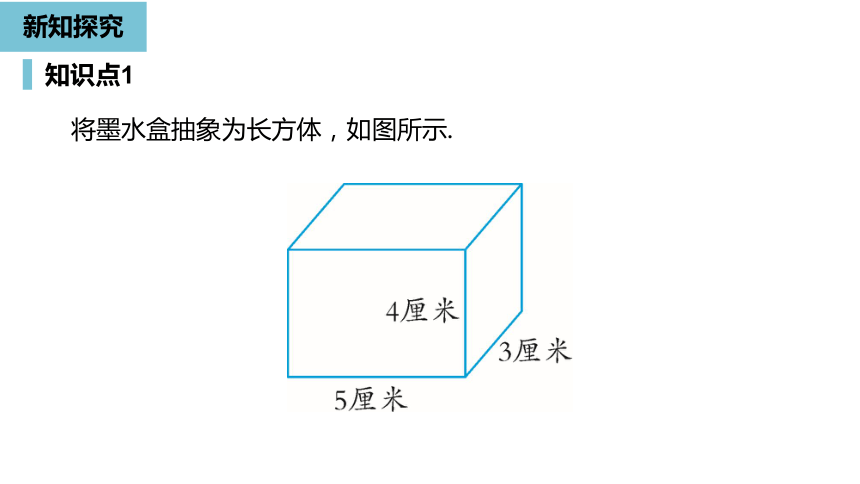
将墨水盒抽象为长方体,如图所示.
知识点1
新知探究
各小组按照自己的设计思路,在一张软纸上设计包装盒的平面草图,裁纸、折叠,观察效果.可以不断调整设计,直至达到设计要求.
知识点1
新知探究
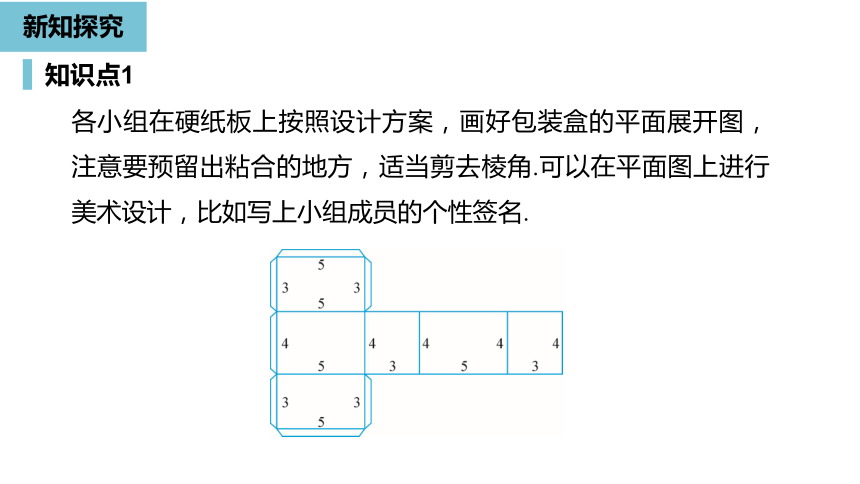
各小组在硬纸板上按照设计方案,画好包装盒的平面展开图,注意要预留出粘合的地方,适当剪去棱角.可以在平面图上进行美术设计,比如写上小组成员的个性签名.
知识点1
新知探究
裁下设计好的平面图形,折叠并粘合,各小组展示成果.
知识点1
新知探究
设计制作一个正五棱柱形状(底面是
5
条边都相等、5个角都相等的五边形)的包装纸盒.
知识点1
新知探究
设计制作一个圆柱形状的包装纸盒.
圆锥
三棱锥
常见几何体的展开图:
四棱锥
长方体
三棱柱
三棱柱
正方体
圆柱
知识点1
新知探究
随堂练习
1
在图上剪去一个图形,剩下的图形可以折叠成一个长方体,则剪去的这个图形是(
)
A.①
B.②
C.③
D.④
A
随堂练习
2
如图所示的平面图形能折叠成的长方体是(
)
A
B
C
D
D
随堂练习
3
下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是(
)
A
B
C
D
A
课堂小结
制作立体图形:
立体图形
平面图形
立体图形
展开
折叠
拓展提升
1
在一次数学活动课上,王老师给学生发了一张长
30
cm,宽
20
cm
的长方形纸片(如图),要求折成一个高为
5
cm
的无盖的且容积最大的长方体盒子,则该盒子的容积是
.
解析:如图所示,
该盒子的容积为
(30-10)×(20-10)×5=1000
(cm3).
1000
cm3
拓展提升
2
仓库里有以下四种规格数量足够多的长方形、正方形的铁片(尺寸单位:分米),从中选5块铁片,焊接成一个无盖的长方体(或正方体)铁盒(不浪费材料),甲型盒是由2块规格①、1块规格②和2块规格③焊接而成的铁盒,乙型盒是容积最小的铁盒.
拓展提升
2
(1)
甲型盒的容积为
立方分米;乙型盒的容积为
立方分米;
解:(1)
因为甲型盒是由2块规格①、1块规格②和2块规格③焊接而成的,
所以甲盒的长为
4
分米,宽为
2
分米,高为
5
分米,
所以甲型盒容积为
2×4×5=40
(立方分米);
乙型盒容积最小,即长、宽、高最小,因此乙盒为长、宽、高均为
2
分米的正方体,体积为
2×2×2=8
(立方分米).
40
8
拓展提升
2
(2)
现取两个装满水的乙型盒,再将其内部所有的水都倒入一个水平放置的甲型盒,求甲型盒中水的高度是多少分米?
解:(2)
甲盒的底面积为
2×4=8
(平方分米),两个乙盒的水的体积为
8×2=16
(立方分米),
所以甲盒内水的高度为
16÷8=2
(分米).
4.4 课题学习
设计制作长方体形状的包装纸盒
几何图形初步
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
面、棱的大小、位置关系
长方体
长方体的平面展开图
展开图中面的位置与立体图形中的位置的对应关系
学习目标
1.
学生能独立完成包装纸盒的制作.
2.
通过制作过程体会立体图形与平面图形的对应关系.
3.
通过体验观察、思考、操作、总结的过程,增强空间能力.
课堂导入
上节课我们通过动手操作把一个长方体盒子拆开得到它的平面展开图,并尝试进行复原,那么怎么在一张纸上画出长方体的平面展开图并折叠成长方体呢?本节课我们将来解决这个问题.
知识点1
新知探究
要得到如图所示的长方体形状的墨水盒,设计方案内容包括:包装盒的形状、尺寸、外表图案等.
知识点1
新知探究
将墨水盒抽象为长方体,如图所示.
知识点1
新知探究
各小组按照自己的设计思路,在一张软纸上设计包装盒的平面草图,裁纸、折叠,观察效果.可以不断调整设计,直至达到设计要求.
知识点1
新知探究
各小组在硬纸板上按照设计方案,画好包装盒的平面展开图,注意要预留出粘合的地方,适当剪去棱角.可以在平面图上进行美术设计,比如写上小组成员的个性签名.
知识点1
新知探究
裁下设计好的平面图形,折叠并粘合,各小组展示成果.
知识点1
新知探究
设计制作一个正五棱柱形状(底面是
5
条边都相等、5个角都相等的五边形)的包装纸盒.
知识点1
新知探究
设计制作一个圆柱形状的包装纸盒.
圆锥
三棱锥
常见几何体的展开图:
四棱锥
长方体
三棱柱
三棱柱
正方体
圆柱
知识点1
新知探究
随堂练习
1
在图上剪去一个图形,剩下的图形可以折叠成一个长方体,则剪去的这个图形是(
)
A.①
B.②
C.③
D.④
A
随堂练习
2
如图所示的平面图形能折叠成的长方体是(
)
A
B
C
D
D
随堂练习
3
下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是(
)
A
B
C
D
A
课堂小结
制作立体图形:
立体图形
平面图形
立体图形
展开
折叠
拓展提升
1
在一次数学活动课上,王老师给学生发了一张长
30
cm,宽
20
cm
的长方形纸片(如图),要求折成一个高为
5
cm
的无盖的且容积最大的长方体盒子,则该盒子的容积是
.
解析:如图所示,
该盒子的容积为
(30-10)×(20-10)×5=1000
(cm3).
1000
cm3
拓展提升
2
仓库里有以下四种规格数量足够多的长方形、正方形的铁片(尺寸单位:分米),从中选5块铁片,焊接成一个无盖的长方体(或正方体)铁盒(不浪费材料),甲型盒是由2块规格①、1块规格②和2块规格③焊接而成的铁盒,乙型盒是容积最小的铁盒.
拓展提升
2
(1)
甲型盒的容积为
立方分米;乙型盒的容积为
立方分米;
解:(1)
因为甲型盒是由2块规格①、1块规格②和2块规格③焊接而成的,
所以甲盒的长为
4
分米,宽为
2
分米,高为
5
分米,
所以甲型盒容积为
2×4×5=40
(立方分米);
乙型盒容积最小,即长、宽、高最小,因此乙盒为长、宽、高均为
2
分米的正方体,体积为
2×2×2=8
(立方分米).
40
8
拓展提升
2
(2)
现取两个装满水的乙型盒,再将其内部所有的水都倒入一个水平放置的甲型盒,求甲型盒中水的高度是多少分米?
解:(2)
甲盒的底面积为
2×4=8
(平方分米),两个乙盒的水的体积为
8×2=16
(立方分米),
所以甲盒内水的高度为
16÷8=2
(分米).
