人教版数学七年级上册4.4课题学习设计制作长方体形状的包装纸盒(1)课件(18张PPT)
文档属性
| 名称 | 人教版数学七年级上册4.4课题学习设计制作长方体形状的包装纸盒(1)课件(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 270.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 16:55:29 | ||
图片预览


文档简介
(共18张PPT)
4.4 课题学习
设计制作长方体形状的包装纸盒
几何图形初步
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
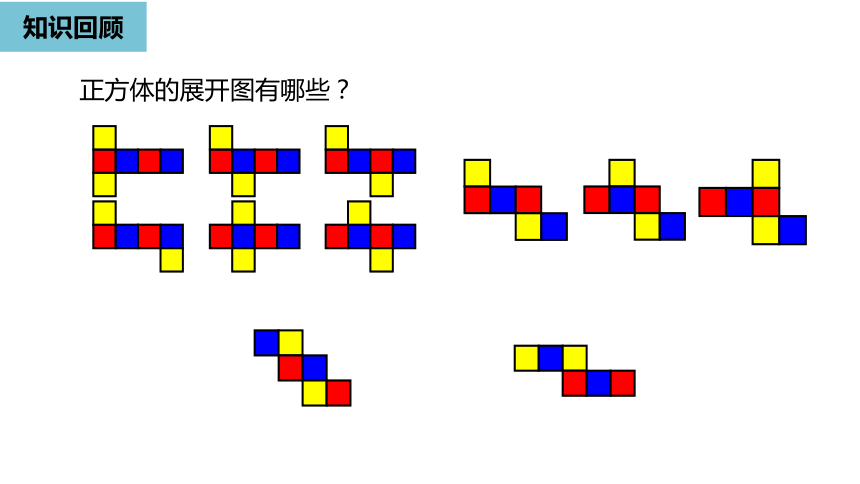
正方体的展开图有哪些?
学习目标
1.
根据实物图进一步了解长方体的特征.
2.掌握长方体展开图的特点.
课堂导入
日常生活中,我们经常可以看到各种各样的长(正)
方体形状的包装盒,如粉笔盒、文具盒、牙膏盒等,
设计这类包装盒时,要先绘制长方体的展开图,再把它剪开并折叠成长方体.
本节中,我们将尝试设计和制作长方体纸盒.
知识点1
新知探究
(1)
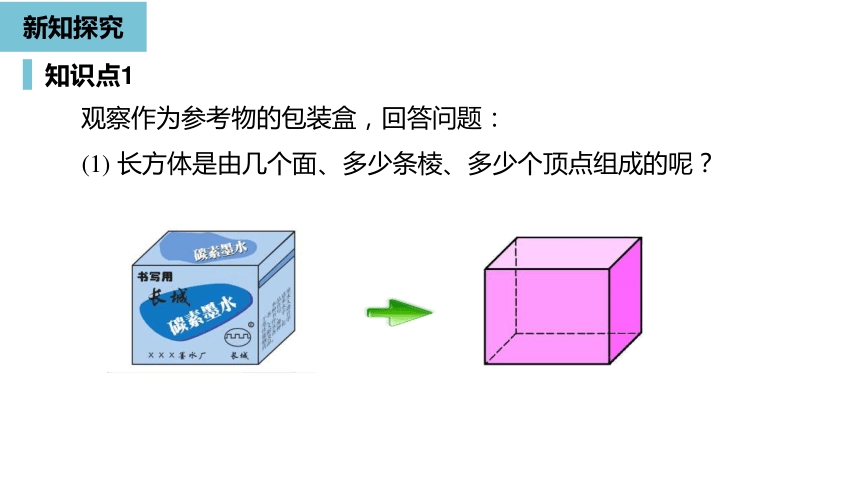
长方体是由几个面、多少条棱、多少个顶点组成的呢?
观察作为参考物的包装盒,回答问题:
知识点1
新知探究
(2)
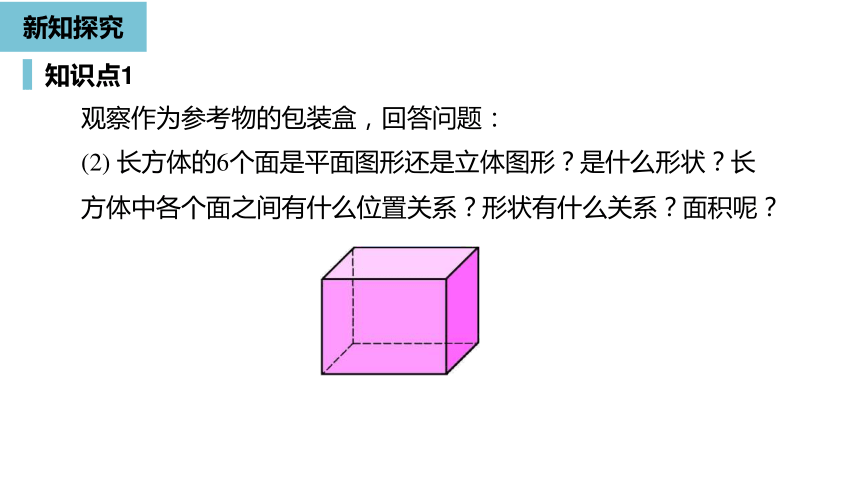
长方体的6个面是平面图形还是立体图形?是什么形状?长方体中各个面之间有什么位置关系?形状有什么关系?面积呢?
观察作为参考物的包装盒,回答问题:
知识点1
新知探究
(3)
长方体的棱的长短和位置有什么特殊的关系呢?
观察作为参考物的包装盒,回答问题:
知识点1
新知探究
拆开观察长方体包装盒的展开图.
展开
(1)
将每一组的纸制长方体沿棱剪开,展开成一个完整的平面展开图,需要剪开多少条棱?
知识点1
新知探究
请各小组到讲台前展示各自的图形.
拆开观察长方体包装盒的展开图.
……
知识点1
新知探究
(2)
所得的平面展开图是什么样的?找出对应长方体各面、棱的相应部分,找出其中的关系.
上
下
前
后
左
右
展开
拆开观察长方体包装盒的展开图.
知识点2
新知探究
观察它是如何折叠并粘到一起的,重点观察一下它是如何折叠的.
还原表面展开图为包装盒.
折叠
跟踪训练
新知探究
某种商品的外包装箱是长方体,其展开图的面积为
430
平方分米(如图),其中
BC=5
分米,EF=10
分米,则
AB
的长度为
分米.
解析:由题意得
2×(5AB+10AB+5×10)=430,
解得
AB=11.
11
1
如图为一无盖长方体盒子的展开图(重叠部分不计),可知该无盖长方体的容积为(
)
A.4
B.6
C.8
D.12
解析:长方体的高是1,宽是3-1=2,长是6-2=4,
长方体的容积是4×2×1=8.
C
随堂练习
随堂练习
2
如图是一个长方体的表面展开图,每个面上都标注了字母和数据,请根据要求回答:
(1)
如果
A
面在长方体的底部,那么
面会在上面;
(2)
求这个长方体的表面积和体积.
解:(2)
这个长方体的表面积是
2×(1×3+1×2+2×3)=22
(平方米).
体积是
1×2×3=6
(立方米).
F
随堂练习
3
如图,一个长方体的表面展开图中四边形
ABCD
是正方形(正方形的四个角都是直角、四条边都相等),则根据图中数据可得原长方体的体积是
cm3.
解析:因为四边形
ABCD
是正方形,
所以AB=AE=5
cm,
所以立方体的高为
(7-5)÷2=1
(cm),
所以EF=5-1=4(cm),
所以原长方体的体积是
5×4×1=20(cm3).
20
课堂小结
面、棱的大小、位置关系
长方体
长方体的平面展开图
展开图中面的位置与立体图形中的位置的对应关系
拓展提升
如图所示是长方体的平面展开图,设
AB=x,若
AD=4x,AN=3x.
(1)
求长方形
DEFG
的周长与长方形
ABMN
的周长(用字母
x
进行表示);
(2)
若长方形
DEFG
的周长比长方形
ABMN
的周长少8,求原长方体的体积.
解:(1)
因为AB=x,若
AD=4x,AN=3x,
所以DG=BC=AD-2AB=4x-2x=2x,
所以长方形
DEFG
的周长为
2(x+2x)=6x,
长方形
ABMN
的周长为
2(x+3x)=8x;
拓展提升
解:(2)
依题意得
8x-6x=8,
解得
x=4,
原长方体的体积为
x·2x·3x=6x3,
将
x=4代入,可得体积
6x3=384.
故原长方体的体积是384.
如图所示是长方体的平面展开图,设
AB=x,若
AD=4x,AN=3x.
(1)
求长方形
DEFG
的周长与长方形
ABMN
的周长(用字母
x
进行表示);
(2)
若长方形
DEFG
的周长比长方形
ABMN
的周长少8,求原长方体的体积.
4.4 课题学习
设计制作长方体形状的包装纸盒
几何图形初步
人教版-数学-七年级上册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
正方体的展开图有哪些?
学习目标
1.
根据实物图进一步了解长方体的特征.
2.掌握长方体展开图的特点.
课堂导入
日常生活中,我们经常可以看到各种各样的长(正)
方体形状的包装盒,如粉笔盒、文具盒、牙膏盒等,
设计这类包装盒时,要先绘制长方体的展开图,再把它剪开并折叠成长方体.
本节中,我们将尝试设计和制作长方体纸盒.
知识点1
新知探究
(1)
长方体是由几个面、多少条棱、多少个顶点组成的呢?
观察作为参考物的包装盒,回答问题:
知识点1
新知探究
(2)
长方体的6个面是平面图形还是立体图形?是什么形状?长方体中各个面之间有什么位置关系?形状有什么关系?面积呢?
观察作为参考物的包装盒,回答问题:
知识点1
新知探究
(3)
长方体的棱的长短和位置有什么特殊的关系呢?
观察作为参考物的包装盒,回答问题:
知识点1
新知探究
拆开观察长方体包装盒的展开图.
展开
(1)
将每一组的纸制长方体沿棱剪开,展开成一个完整的平面展开图,需要剪开多少条棱?
知识点1
新知探究
请各小组到讲台前展示各自的图形.
拆开观察长方体包装盒的展开图.
……
知识点1
新知探究
(2)
所得的平面展开图是什么样的?找出对应长方体各面、棱的相应部分,找出其中的关系.
上
下
前
后
左
右
展开
拆开观察长方体包装盒的展开图.
知识点2
新知探究
观察它是如何折叠并粘到一起的,重点观察一下它是如何折叠的.
还原表面展开图为包装盒.
折叠
跟踪训练
新知探究
某种商品的外包装箱是长方体,其展开图的面积为
430
平方分米(如图),其中
BC=5
分米,EF=10
分米,则
AB
的长度为
分米.
解析:由题意得
2×(5AB+10AB+5×10)=430,
解得
AB=11.
11
1
如图为一无盖长方体盒子的展开图(重叠部分不计),可知该无盖长方体的容积为(
)
A.4
B.6
C.8
D.12
解析:长方体的高是1,宽是3-1=2,长是6-2=4,
长方体的容积是4×2×1=8.
C
随堂练习
随堂练习
2
如图是一个长方体的表面展开图,每个面上都标注了字母和数据,请根据要求回答:
(1)
如果
A
面在长方体的底部,那么
面会在上面;
(2)
求这个长方体的表面积和体积.
解:(2)
这个长方体的表面积是
2×(1×3+1×2+2×3)=22
(平方米).
体积是
1×2×3=6
(立方米).
F
随堂练习
3
如图,一个长方体的表面展开图中四边形
ABCD
是正方形(正方形的四个角都是直角、四条边都相等),则根据图中数据可得原长方体的体积是
cm3.
解析:因为四边形
ABCD
是正方形,
所以AB=AE=5
cm,
所以立方体的高为
(7-5)÷2=1
(cm),
所以EF=5-1=4(cm),
所以原长方体的体积是
5×4×1=20(cm3).
20
课堂小结
面、棱的大小、位置关系
长方体
长方体的平面展开图
展开图中面的位置与立体图形中的位置的对应关系
拓展提升
如图所示是长方体的平面展开图,设
AB=x,若
AD=4x,AN=3x.
(1)
求长方形
DEFG
的周长与长方形
ABMN
的周长(用字母
x
进行表示);
(2)
若长方形
DEFG
的周长比长方形
ABMN
的周长少8,求原长方体的体积.
解:(1)
因为AB=x,若
AD=4x,AN=3x,
所以DG=BC=AD-2AB=4x-2x=2x,
所以长方形
DEFG
的周长为
2(x+2x)=6x,
长方形
ABMN
的周长为
2(x+3x)=8x;
拓展提升
解:(2)
依题意得
8x-6x=8,
解得
x=4,
原长方体的体积为
x·2x·3x=6x3,
将
x=4代入,可得体积
6x3=384.
故原长方体的体积是384.
如图所示是长方体的平面展开图,设
AB=x,若
AD=4x,AN=3x.
(1)
求长方形
DEFG
的周长与长方形
ABMN
的周长(用字母
x
进行表示);
(2)
若长方形
DEFG
的周长比长方形
ABMN
的周长少8,求原长方体的体积.
