人教版初一数学下册9.3一元一次不等式组解法综合运用课件(44张)
文档属性
| 名称 | 人教版初一数学下册9.3一元一次不等式组解法综合运用课件(44张) |  | |
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-30 12:26:16 | ||
图片预览










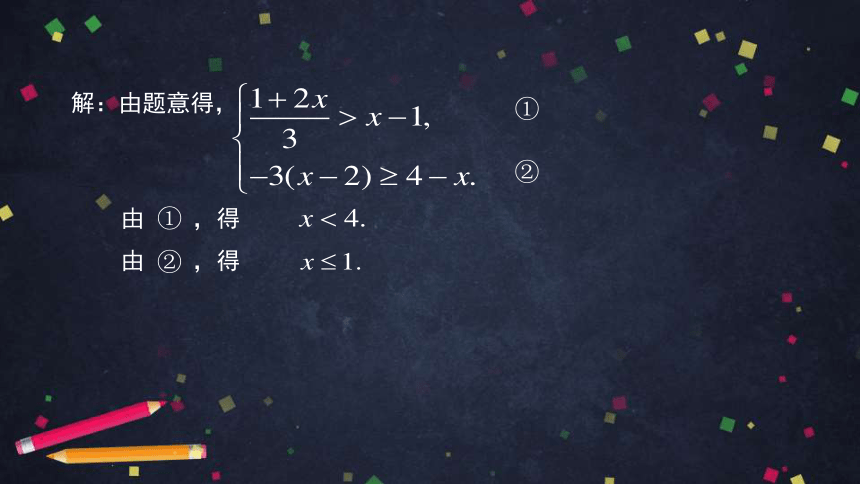

文档简介
(共44张PPT)
初一年级
数学
一元一次不等式组解法综合运用
x取哪些整数值时,不等式
与
都成立?
例
题
x取哪些整数值时,不等式
与
都成立?
分析:“都成立”说明x同时满足两个不等式,
解集中的整数值.
①
②
解:由题意得,
由
,得
①
②
由
,得
①
②
由
,得
①
解:由题意得,
由
,得
②
①
②
由
,得
①
解:由题意得,
由
,得
②
所以不等式组的解集为
0
?1
1
2
3
4
?2
?3
①
②
由
,得
①
解:由题意得,
由
,得
②
所以不等式组的解集为
所以x可取的整数值是?2,
?1,0,1,2,3,4.
0
?1
1
2
3
4
?2
?3
列不等式组
解不等式组
解集中的特殊值
x取哪些整数值时,
不等式
与
都成立?
整数值是?2,
?1,0,1,2,3,4.
x取哪些非负整数值时,不等式
与
练
习
都成立?
x取哪些非负整数值时,不等式
与
都成立?
解集中的非负整数值.
分析:“都成立”说明x同时满足两个不等式,
0和正整数
②
由
,得
①
②
解:由题意得,
由
,得
①
②
由
,得
①
②
解:由题意得,
由
,得
①
1
0
2
3
4
5
?1
所以不等式组的解集为
所以x可取的非负整数值是
0,1.
例
题
把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本?共有多少人?
把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本?共有多少人?
把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本?共有多少人?
设共有x人
前面有(
x
?1)人
最后一人
分5(
x
?1)本;
共(3
x
+8)本;
[(3
x
+8)
?
5(
x
?1)]
本.
分析:
人
书
把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本?共有多少人?
最后一人分的书有[(3
x
+8)
?
5(
x
?1)]
本,
“不到”表明“<”
书不能为负数
(3
x
+8)
?
5(
x
?1)<3;
分析:
(3
x
+8)
?
5(
x
?1)≥0;
把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本?共有多少人?
分析:
答:这些书有26本,共有6人.
解:设有x名学生,则有(3
x
+8)本书,
所以x
=
6.
3
x
+8=26.
由题意,得
①
②
由
,得
①
②
由
,得
2
1
3
4
5
6
0
7
所以不等式组的解集为
利用不等式组解决实际问题的一般步骤:
6
答
3
列
5
验
2
设
1
审
4
解
例
题
(1)当m
时,关于x的不等式组
的解集是
x<2;
(2)当m
时,关于x的不等式组
无解.
(1)当m
时,关于x的不等式组
的解集是
x<2;
2
m
2
m
2
(m)
(1)当m
时,关于x的不等式组
的解集是
x<2;
2
m
2
m
2
(m)
当
m
<
2
时
x
<
m
当
m
>
2
时
x
<
2
当
m
=
2
时
x
<
2
≥
2
(2)当m
时,关于x的不等式组
无解.
2
m
2
m
2
(m)
当
m
<
2
时
当
m
>
2
时
当
m
=
2
时
(2)当m
时,关于x的不等式组
无解.
2
m
2
m
2
(m)
当
m
<
2
时
当
m
>
2
时
当
m
=
2
时
2
<
x
<
m
无解
2
解关于x的不等式组
2
解关于x的不等式组
(m)
形
这两个点
重合时
无公共部分
m
=
2
时
不等式组无解
数
(2)当m
时,关于x的不等式组
无解.
2
m
2
m
2
(m)
当
m
<
2
时
当
m
>
2
时
当
m
=
2
时
2
<
x
<
m
无解
无解
≤
2
例
题
2
m
5<
m
<6
m
2
1
3
4
5
6
0
如果关于x的不等式组
恰好有3个整数解,那么m的取值范围是
.
当m
>
2时
2<
x
5<
m
<6
当
m
=
5
时
当
m
=
6
时
综上,5<
m
≤6.
(m)
2
1
3
4
5
6
0
(m)
2
1
3
4
5
6
0
m
2
1
3
4
5
6
0
不符合题意
符合题意
如果关于x的不等式组
恰好有3个整数解,那么m的取值范围是
.
5<
m
≤6
画数轴
确定范围
验边界
结论
m
2
1
3
4
5
6
0
5<
m
<6
(m)
2
1
3
4
5
6
0
当
m
=
5
时
(m)
2
1
3
4
5
6
0
当
m
=
6
时
综上,5<
m
≤6.
例
题
已知a是自然数,关于x的不等式组
的解集是x
>
2,则a的值是
.
已知a是自然数,关于x的不等式组
的解集是x
>
2,则a的值是
.
已知a是自然数,关于x的不等式组
的解集是x
>
2,则a的值是
.
2
2
2
当
=
2
时
当
>
2
时
当
<
2
时
2
解关于x的不等式组
形
这两个点
重合时
=2时
数
已知a是自然数,关于x的不等式组
的解集是x
>
2,则a的值是
.
2
2
2
当
=
2
时
当
>
2
时
当
<
2
时
综上,
≤
2
.
解得
a
≤
2.
自然数a
=0,1,2.
0,1,2
当a
时,关于x的不等式组
的解集为x
<
4.
练
习
4
a
当
a
<
4
时
x
<
a
4
a
当
a
>
4
时
4
(a)
当
a
=
4
时
x
<
4
x
<
4
≥
4
例
题
已知关于x的不等式组
恰好有3个整数解,
则a的取值范围是
.
3a?2
1
当
3a?2
<
1
时
3a?2
?2
?3
?1
0
1
2
?4
3a?2
<
x
<1
?3
<
3a?2
<
?2
已知关于x的不等式组
恰好有3个整数解,
则a的取值范围是
.
3a?2
?2
?3
?1
0
1
2
?4
?3
<
3a?2
<
?2
3a?2
?2
?3
?1
0
1
2
?4
3a?2
?2
?3
?1
0
1
2
?4
当3a?2
=
?3
时
当3a?2
=
?2
时
不符合题意
符合题意
综上,
?3
≤
3a?2
<
?2
.
解?3
≤
3a?2
<
?2
解:(方法1)解不等式组
得
(方法2)利用不等式的性质
各边同时加2,得
?3+2
≤
3a
<
?2+2,
?1
≤
3a
<
0,
各边同时除以3,得
已知关于x的不等式组
恰好有3个整数解,
则a的取值范围是
.
3a?2
?2
?3
?1
0
1
2
?4
?3
<
3a?2
<
?2
3a?2
?2
?3
?1
0
1
2
?4
3a?2
?2
?3
?1
0
1
2
?4
当3a?2
=
?3
时
当3a?2
=
?2
时
不符合题意
符合题意
综上,
?3
≤
3a?2
<
?2
.
解得,
x取哪些整数值时,
不等式
与
都成立?
整数值是?2,
?1,0,1,2,3,4.
总
结
1.
将条件转化成解不等式组,解决问题.
2.利用不等式组解决实际问题.
6
答
3
列
5
验
2
设
1
审
4
解
当a
时,关于x的不等式组
的解集为x
<
4.
综上,a
≥
4.
4
a
当
a
<
4
时
x
<
a
4
a
当
a
>
4
时
4
(a)
当
a
=
4
时
x
<
4
x
<
4
≥
4
3.已知不等式组的解集或特殊解,确定字母的取值范围.
注意验边界
作
业
1.
x
取哪些整数值时,不等式
与
都成立?
2.
x
取哪些整数值时,
成立
?
3.
的值能否同时大于
2
x
+
3
和
1
?
x
的值?
人教版教材《数学七年级下册》第130页第3题、第4题,第133页第4题.
初一年级
数学
一元一次不等式组解法综合运用
x取哪些整数值时,不等式
与
都成立?
例
题
x取哪些整数值时,不等式
与
都成立?
分析:“都成立”说明x同时满足两个不等式,
解集中的整数值.
①
②
解:由题意得,
由
,得
①
②
由
,得
①
②
由
,得
①
解:由题意得,
由
,得
②
①
②
由
,得
①
解:由题意得,
由
,得
②
所以不等式组的解集为
0
?1
1
2
3
4
?2
?3
①
②
由
,得
①
解:由题意得,
由
,得
②
所以不等式组的解集为
所以x可取的整数值是?2,
?1,0,1,2,3,4.
0
?1
1
2
3
4
?2
?3
列不等式组
解不等式组
解集中的特殊值
x取哪些整数值时,
不等式
与
都成立?
整数值是?2,
?1,0,1,2,3,4.
x取哪些非负整数值时,不等式
与
练
习
都成立?
x取哪些非负整数值时,不等式
与
都成立?
解集中的非负整数值.
分析:“都成立”说明x同时满足两个不等式,
0和正整数
②
由
,得
①
②
解:由题意得,
由
,得
①
②
由
,得
①
②
解:由题意得,
由
,得
①
1
0
2
3
4
5
?1
所以不等式组的解集为
所以x可取的非负整数值是
0,1.
例
题
把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本?共有多少人?
把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本?共有多少人?
把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本?共有多少人?
设共有x人
前面有(
x
?1)人
最后一人
分5(
x
?1)本;
共(3
x
+8)本;
[(3
x
+8)
?
5(
x
?1)]
本.
分析:
人
书
把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本?共有多少人?
最后一人分的书有[(3
x
+8)
?
5(
x
?1)]
本,
“不到”表明“<”
书不能为负数
(3
x
+8)
?
5(
x
?1)<3;
分析:
(3
x
+8)
?
5(
x
?1)≥0;
把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本?共有多少人?
分析:
答:这些书有26本,共有6人.
解:设有x名学生,则有(3
x
+8)本书,
所以x
=
6.
3
x
+8=26.
由题意,得
①
②
由
,得
①
②
由
,得
2
1
3
4
5
6
0
7
所以不等式组的解集为
利用不等式组解决实际问题的一般步骤:
6
答
3
列
5
验
2
设
1
审
4
解
例
题
(1)当m
时,关于x的不等式组
的解集是
x<2;
(2)当m
时,关于x的不等式组
无解.
(1)当m
时,关于x的不等式组
的解集是
x<2;
2
m
2
m
2
(m)
(1)当m
时,关于x的不等式组
的解集是
x<2;
2
m
2
m
2
(m)
当
m
<
2
时
x
<
m
当
m
>
2
时
x
<
2
当
m
=
2
时
x
<
2
≥
2
(2)当m
时,关于x的不等式组
无解.
2
m
2
m
2
(m)
当
m
<
2
时
当
m
>
2
时
当
m
=
2
时
(2)当m
时,关于x的不等式组
无解.
2
m
2
m
2
(m)
当
m
<
2
时
当
m
>
2
时
当
m
=
2
时
2
<
x
<
m
无解
2
解关于x的不等式组
2
解关于x的不等式组
(m)
形
这两个点
重合时
无公共部分
m
=
2
时
不等式组无解
数
(2)当m
时,关于x的不等式组
无解.
2
m
2
m
2
(m)
当
m
<
2
时
当
m
>
2
时
当
m
=
2
时
2
<
x
<
m
无解
无解
≤
2
例
题
2
m
5<
m
<6
m
2
1
3
4
5
6
0
如果关于x的不等式组
恰好有3个整数解,那么m的取值范围是
.
当m
>
2时
2<
x
m
<6
当
m
=
5
时
当
m
=
6
时
综上,5<
m
≤6.
(m)
2
1
3
4
5
6
0
(m)
2
1
3
4
5
6
0
m
2
1
3
4
5
6
0
不符合题意
符合题意
如果关于x的不等式组
恰好有3个整数解,那么m的取值范围是
.
5<
m
≤6
画数轴
确定范围
验边界
结论
m
2
1
3
4
5
6
0
5<
m
<6
(m)
2
1
3
4
5
6
0
当
m
=
5
时
(m)
2
1
3
4
5
6
0
当
m
=
6
时
综上,5<
m
≤6.
例
题
已知a是自然数,关于x的不等式组
的解集是x
>
2,则a的值是
.
已知a是自然数,关于x的不等式组
的解集是x
>
2,则a的值是
.
已知a是自然数,关于x的不等式组
的解集是x
>
2,则a的值是
.
2
2
2
当
=
2
时
当
>
2
时
当
<
2
时
2
解关于x的不等式组
形
这两个点
重合时
=2时
数
已知a是自然数,关于x的不等式组
的解集是x
>
2,则a的值是
.
2
2
2
当
=
2
时
当
>
2
时
当
<
2
时
综上,
≤
2
.
解得
a
≤
2.
自然数a
=0,1,2.
0,1,2
当a
时,关于x的不等式组
的解集为x
<
4.
练
习
4
a
当
a
<
4
时
x
<
a
4
a
当
a
>
4
时
4
(a)
当
a
=
4
时
x
<
4
x
<
4
≥
4
例
题
已知关于x的不等式组
恰好有3个整数解,
则a的取值范围是
.
3a?2
1
当
3a?2
<
1
时
3a?2
?2
?3
?1
0
1
2
?4
3a?2
<
x
<1
?3
<
3a?2
<
?2
已知关于x的不等式组
恰好有3个整数解,
则a的取值范围是
.
3a?2
?2
?3
?1
0
1
2
?4
?3
<
3a?2
<
?2
3a?2
?2
?3
?1
0
1
2
?4
3a?2
?2
?3
?1
0
1
2
?4
当3a?2
=
?3
时
当3a?2
=
?2
时
不符合题意
符合题意
综上,
?3
≤
3a?2
<
?2
.
解?3
≤
3a?2
<
?2
解:(方法1)解不等式组
得
(方法2)利用不等式的性质
各边同时加2,得
?3+2
≤
3a
<
?2+2,
?1
≤
3a
<
0,
各边同时除以3,得
已知关于x的不等式组
恰好有3个整数解,
则a的取值范围是
.
3a?2
?2
?3
?1
0
1
2
?4
?3
<
3a?2
<
?2
3a?2
?2
?3
?1
0
1
2
?4
3a?2
?2
?3
?1
0
1
2
?4
当3a?2
=
?3
时
当3a?2
=
?2
时
不符合题意
符合题意
综上,
?3
≤
3a?2
<
?2
.
解得,
x取哪些整数值时,
不等式
与
都成立?
整数值是?2,
?1,0,1,2,3,4.
总
结
1.
将条件转化成解不等式组,解决问题.
2.利用不等式组解决实际问题.
6
答
3
列
5
验
2
设
1
审
4
解
当a
时,关于x的不等式组
的解集为x
<
4.
综上,a
≥
4.
4
a
当
a
<
4
时
x
<
a
4
a
当
a
>
4
时
4
(a)
当
a
=
4
时
x
<
4
x
<
4
≥
4
3.已知不等式组的解集或特殊解,确定字母的取值范围.
注意验边界
作
业
1.
x
取哪些整数值时,不等式
与
都成立?
2.
x
取哪些整数值时,
成立
?
3.
的值能否同时大于
2
x
+
3
和
1
?
x
的值?
人教版教材《数学七年级下册》第130页第3题、第4题,第133页第4题.
