2019—2020学年教科版选修3-1 磁场 章末复习精炼2(解析版)
文档属性
| 名称 | 2019—2020学年教科版选修3-1 磁场 章末复习精炼2(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 625.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-20 00:00:00 | ||
图片预览




文档简介
2019—2020学年教科版
选修3-1磁场
章末复习精炼(解析版)
1.2020年爆发了新冠肺炎,该病毒传播能力非常强,因此研究新冠肺炎病毒株的实验室必须是全程都在高度无接触物理防护性条件下操作。武汉病毒研究所是我国防护等级最高的P4实验室,在该实验室中有一种污水流量计,其原理可以简化为如右图所示模型:废液内含有大量正、负离子,从直径为d的圆柱形容器右侧流入,左侧流出。流量值Q等于单位时间通过横截面的液体的体积。空间有垂直纸面向里的磁感应强度为B的匀强磁场,下列说法正确的是( )
A.带电粒子所受洛伦兹力方向是水平向左
B.正、负粒子所受洛伦兹力方向是相同的
C.污水流量计也可以用于测量不带电的液体的流速
D.只需要测量MN两点电压就能够推算废液的流量
2.湖北武当山金殿,以前在雷雨交加时,金殿的屋顶常会出现盆大的火球,来回滚动。雨过天晴时,大殿金光灿灿,像被重新炼洗过一般,这就是人们所说的“雷火炼殿”奇观。近些年为了保护古建筑,在金殿顶部安装了避雷针,此后,雷火炼殿的奇观消失了。假设某次雷雨时,有一团带大量负电荷的乌云经过其正上方时,发生放电现象。下列说法正确的是( )
A.通过避雷针的电流,方向是从云到殿
B.通过避雷针的电流,不受安培力
C.通过避雷针的电流,所受安培力方向偏西
D.通过避雷针的电流,所受安培力方向竖直向下
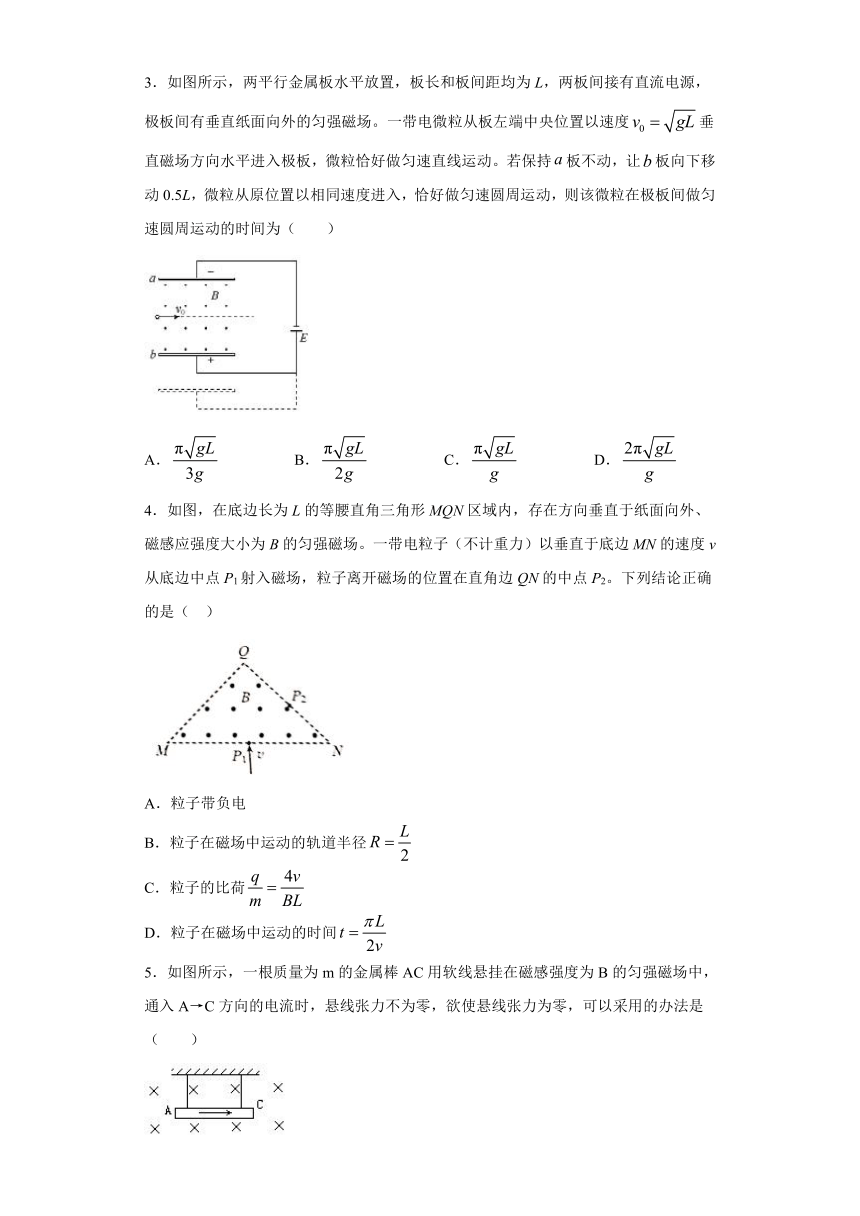
3.如图所示,两平行金属板水平放置,板长和板间距均为L,两板间接有直流电源,极板间有垂直纸面向外的匀强磁场。一带电微粒从板左端中央位置以速度垂直磁场方向水平进入极板,微粒恰好做匀速直线运动。若保持板不动,让板向下移动0.5L,微粒从原位置以相同速度进入,恰好做匀速圆周运动,则该微粒在极板间做匀速圆周运动的时间为( )
A.
B.
C.
D.
4.如图,在底边长为L的等腰直角三角形MQN区域内,存在方向垂直于纸面向外、磁感应强度大小为B的匀强磁场。一带电粒子(不计重力)以垂直于底边MN的速度v从底边中点P1射入磁场,粒子离开磁场的位置在直角边QN的中点P2。下列结论正确的是(
)
A.粒子带负电
B.粒子在磁场中运动的轨道半径
C.粒子的比荷
D.粒子在磁场中运动的时间
5.如图所示,一根质量为m的金属棒AC用软线悬挂在磁感强度为B的匀强磁场中,通入A→C方向的电流时,悬线张力不为零,欲使悬线张力为零,可以采用的办法是
(
)
A.不改变电流和磁场方向,适当增大电流
B.只改变电流方向,并适当减小电流
C.不改变磁场和电流方向,适当减小磁感强度
D.同时改变磁场方向,并适当减小磁感强度
6.如图所示,在直角三角形ABC内存在垂直纸面向外的匀强磁场,AC
=
d,∠B
=
30°。现垂直AB边射入一群质量均为m、电荷量均为q、速度大小均为v的带正电粒子,已知垂直AC边射出的粒子在磁场中运动的时间均为t,而在磁场中运动的最长时间为
(不计重力和粒子间的相互作用)。下列判断正确的是( )
A.粒子在磁场中做匀速圆周运动的周期为4t
B.该匀强磁场的磁感应强度大小为
C.粒子在进入磁场时速度大小为
D.粒子在磁场中运动的轨迹半径为
7.如图所示,一个边长为l的正六边形的区域内有匀强磁场,匀强磁场的磁感应强度大小为B、方向垂直于纸面向外。在点处的粒子源发出大量质量为电荷量为的同种粒子,粒子的速度大小不同,方向始终沿方向。不计粒子间的相互作用力及重力,下列说法正确的是( )
A.速度小于的粒子在磁场中运动的时间一定相同
B.速度大于的粒子一定打在边上
C.经过点的粒子在磁场中运动的时间为
D.垂直打在边上的粒子在磁场中运动的时间为
8.如图所示,质量均为m的物块a、b用一根劲度系数为k的轻弹簧相连接,放在倾角为θ的足够长光滑固定斜面上,且a是带电量为+q的绝缘物块,b不带电,C为固定挡板.整个装置处于磁感应强度大小为B、方向垂直纸面向里的匀强磁场中,系统处于静止状态.现用一外力F沿斜面方向拉物块a使之向上做匀加速运动,当物块a刚要离开斜面时物块b恰将离开挡板C.重力加速度大小为g,则此过程中
A.物块a运动的距离为
B.b刚要离开挡板时弹簧弹力为2mgsinθ
C.外力F做的功为
D.物块a运动的时间为
9.如图,正方形abcd区域内有垂直纸面的匀强磁场。a点处的粒子源沿ac方向发出大量相同的带电粒子,粒子的速度大小不同。当粒子速度为v0时恰好从e点垂直cd边射出,不计粒子间的相互作用力及重力,下列说法正确的是( )
A.e点为cd边的中点
B.速度为时,粒子从d点射出
C.速度小于的所有粒子在磁场中运动的路程与速度大小成正比
D.从e点射出的粒子和从d点射出的粒子在磁场中运动的时间之比为2:1
10.南极考察队队员在地球南极附近用弹簧秤竖直悬挂一未通电螺线管,如图所示,下列说法正确的是( )
A.若将a端接电源正极,b端接电源负极,则弹簧秤示数将减小
B.若将a端接电源正极,b端接电源负极,则弹簧秤示数将增大
C.若将b端接电源正极,a端接电源负极,则弹簧秤示数将增大
D.不论螺线管通电情况如何,弹簧秤示数均不变
11.如图所示,质量为m、电荷量为q的带电粒子(不计重力),以速度v沿垂直于磁场的方向进入一匀强磁场区域,并在磁场中做匀速圆周运动。已知磁场的磁感应强度为B,则该粒子做匀速圆周运动的轨道半径为____________
,周期为_____________。
12.如图,两根互相平行的长直导线M、N垂直穿过纸面,导线中通有大小相等、方向相反的电流,A、O、B在MN连线上,且将连线四等分。已知直线电流I产生磁场的磁感应强度分布规律是(k为比例系数,为磁场中某点到直导线的距离),现测得O点磁感应强度的大小为3T,则A点的磁感应强度大小为__________T。直导线M受到的磁场力是由_________产生的磁场对其施加的。
13.如图,在纸面内有一圆心为O、半径为R的圆,圆形区域内存在斜向上的电场,电场强度大小未知,区域外存在垂直于纸面向外的匀强磁场,磁感应强度大小为B,一质量为m、电荷量为q的正粒子从圆外P点在纸面内垂直于OP射出,已知粒子从Q点(未画出)进入圆形区域时速度垂直Q点的圆弧切线,随后在圆形区域内运动,并从N点(ON连线的方向与电场方向一致,ON与PO的延长线夹角)射出圆形区域,不计粒子重力,已知OP=3R
(1)求粒子第一次在磁场中运动的速度大小;
(2)求电场强度和粒子射出电场时的速度大小。
14.如图所示,两块平行极板AB、CD正对放置,极板CD的正中央有一小孔,两极板间距离AD为2h,板长AB为4h,两极板间电势差为U,在ABCD构成的矩形区域内存在匀强电场,电场方向水平向右。在ABCD矩形区域外有垂直于纸面向里的范围足够大的匀强磁场。极板厚度不计,电场、磁场的交界处为理想边界。将一个质量为m、电荷量为+q的带电粒子在极板AB的正中央O点由静止释放,带电粒子能够垂直电场方向再次进入匀强电场,带电粒子的重力不计。
(1)求磁场的磁感应强度B的大小;
(2)求出带电粒子从O点开始运动到第二次离开电场区域所经历的总时间;
(3)通过分析说明带电粒子最后能否返回最初的出发点O,若能,请画出粒子运动轨迹的示意图并出带电粒子从O点开始运动到最终返回O点所经历的总时间。若不能,请说明理由。
15.如图所示,竖直平面直角坐标系第一象限有垂直于该竖直面、磁感应强度未知的圆形匀强磁场区域,圆形磁场边界与Y轴上的A(0,cm)点相切;第四象限有充满整个象限水平向左大小的匀强电场。现一质量m=2×10-4kg、带电量为q=+C的微粒从A点以v=4m/s垂直于Y轴沿+X方向射入圆形磁场,经圆形磁场作用后最终从B(10cm,0)点离开第一象限进入第四象限,进入第四象限时速度与X轴正方向成θ=60°(微粒重力不计)。求:
(1)圆形磁场磁感应强度大小及方向;
(2)微粒在第四象限内的轨迹方程(即x关于y的函数);
(3)微粒从A开始运动到再次经过Y轴所经历的时间。
16.如图所示为质谱仪的构造原理图,它是一种分离和检测不同同位素的重要工具。质子数相同而中子数不同的同一元素的不同核素互称为同位素。现让待测的不同带电粒子经加速后进入速度选择器,速度选择器的平行金属板之间有相互正交的匀强磁场和匀强电场(图中未画出),磁感应强度为B,电场强度为E。金属板靠近平板S,在平板S上有可让粒子通过的狭缝P,带电粒子经过速度选择器后,立即从P点沿垂直平板S且垂直于磁场方向的速度进入磁感应强度为B0、并以平板S为边界的有界匀强磁场中,在磁场中偏转后打在记录它的照相底片上,底片厚度可忽略不计,且与平板S重合。根据粒子打在底片上的位置,便可以对它的比荷(电荷量与质量之比)情况进行分析。在下面的讨论中,磁感应强度为B0的匀强磁场区域足够大,空气阻力、带电粒子所受的重力及它们之间的相互作用力均可忽略不计。
(1)若某带电粒子打在底片上的A点,测得P与A之间的距离为x,求该粒子的比荷;
(2)若有两种质量不同的正一价离子,质量分别为m1和m2,它们经速度选择器和匀强磁场后,分别打在底片上的A1和A2两点,测得P到A2的距离与A1到A2的距离相等,求这两种离子的质量之比;
(3)若用这个质谱仪分别观测氢的两种同位素离子(所带电荷量为e),它们分别打在照相底片上相距为d的两点;
①为了便于观测,希望d的数值大一些为宜。试分析说明为了便于观测,应如何改变匀强磁场磁感应强度B0的大小;
②研究小组的同学对上述B0影响d的问题进行了深入的研究。为了直观,他们以d为纵坐标、以为横坐标,画出了d随变化的关系图像,该图像为一条过原点的直线。测得该直线的斜率为k,求这两种同位素离子的质量之差Δm。
参考答案
1.D
【解析】
A.根据左手定则,正电荷受到竖直向下的洛伦兹力,负电荷受到竖直向上的洛伦兹力,AB错误;
C.不带电液体在磁场中流动时,由于没有自由电荷,不能形成电场,MN两点没有电势差,因此无法测出流速,C错误;
D.计算液体的流速,根据
可得流速
流量
D正确。
故选D。
2.C
【解析】
A.电流的方向为正电荷移动的方向与负电荷移动方向相反,大量负电荷从云通过避雷针,说明电流方向是从殿到云,A错误;
BCD.地磁场大致方向是从南到北,根据左手定则,其所受安培力方向偏西,C正确,BD错误。
故选C。
3.A
【解析】
微粒恰好做匀速直线运动时有
恰好做匀速圆周运动
联立解得
即
由题意可知,则有
由公式
得
联立解得
微粒运动轨迹如图所示,由几何关系可得
所以微粒在磁场中运动的时间为
故A正确,BCD错误。
故选A。
4.C
【解析】
A.由题意,可知粒子从P1点进,从P2点出,则粒子向右偏转,根据左手定则可知,粒子带正电,故A错误;
BC.根据题意作出粒子的运动轨迹,如图所示
由题意知,,底边,则根据几何关系可知
,
由题知,为等腰直角三角形,则,在中,根据余弦定理有
解得
粒子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力,则有
解得粒子的比荷,故B错误,C正确;
D.因半径,则由几何关系可得
故,且,所以,故粒子在磁场中偏转的角度也为,则粒子在磁场中运动的时间为
又
解得,故D错误。
故选C。
5.A
【解析】
对导体棒,由平衡知识可知T+F安=mg;若不改变电流和磁场方向,适当增大电流,可增大安培力,能使悬线张力为零.故A正确;只改变电流方向,金属棒所受安培力方向向下,悬线张力一定不为零.故B错误;不改变磁场和电流方向,适当减小磁感应强度,则安培力减小,悬线张力一定不为零.故C错误;同时改变磁场和电流方向,安培力的方向不变,但适当减小磁感应强度会使安培力减小,悬线张力一定不为零.故D错误;故选A.
6.ABD
【解析】
A.带电粒子在磁场中做匀速圆周运动,垂直AC边射出的粒子在磁场中运动的时间是,即
则得周期
选项A正确;
B.由得
故B正确。
D.设运动时间最长的粒子在磁场中的运动轨迹所对的圆心角为,则有
解得
画出该粒子的运动轨迹如图:
设轨道半径为R,由几何知识得
可得
选项D正确;
C.根据线速度的定义有
选项C错误。
故选ABD。
7.ACD
【解析】
A.根据几何关系,粒子恰好经过点时运动半径
由
可知速度
则速度小于的粒子均从边离开磁场,根据几何关系可知转过的圆心角均为,运动时间均为
为粒子在磁场中的运动周期,A正确;
BC.粒子恰好经过点时运动半径
根据几何关系可知运动时间
速度
则速度大于的粒子一定打在边上,B错误,C正确;
D.粒子垂直打在边上时,如图:
根据几何关系可知圆心角为,运动时间
D正确。
故选ACD。
8.AD
【解析】
A.刚开始时,弹簧处于压缩状态,弹簧弹力大小:,物块b恰将离开挡板时,弹簧处于伸长状态,弹簧弹力大小:.整个过程弹簧形变量即a的运动距离,A正确
B.b刚要离开挡板时对b分析有弹簧弹力:,B错误
CD.物块a刚要离开斜面时,垂直于斜面方向有,解得:,物块a匀加速,有,,联立解得:;整个过程的初末状态弹簧的弹性势能大小相等,根据动能定理得:解得:,C错误D正确
9.BC
【解析】
A.当粒子速度为v0时恰好从e点垂直cd边射出时,由几何关系可得
则
所以e点不是cd边的中点,故A错误;
B.由公式
得
速度为时,半径变为
设粒子从d点射出,此时弦长为
则假设成立,故B正确;
C.速度小于的所有粒子均从ad边射出,则粒子的偏转角相同,所以
故C正确;
D.从e点射出的粒子的偏转角为,从d点射出的粒子的弦切角为,则从d点射出的粒子的偏转角为弦切角的两倍,由
可知,从e点射出的粒子和从d点射出的粒子在磁场中运动的时间之比为1:2,故D错误。
故选BC。
10.AC
【解析】
AB.若将端接电源正极,端接电源负极,则根据安培定则可知,螺线管的下端是磁场的N极,磁场的方向向下;又南极附近的磁场的方向向上,所以螺旋管将受到排斥力,弹簧测力计示数将减小,故A正确,B错误;
C.若将端接电源正极,端接电源负极,则根据安培定则可知,螺线管的上端是磁场的N极,磁场的方向向上;又南极附近的磁场的方向向上,所以螺旋管将受到吸引力,弹簧测力计示数将增大,故C正确;
D.由上分析可知,故D错误;
故选AC。
11.
【解析】
[1][2]带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,故有
且有
解得
,
12.4
直导线N
【解析】
[1]设MN的距离为L,根据两通电直导线在O的磁场由右手螺旋定则知均竖直向下,磁感应强度的大小为两同向合成,有
同理A点的磁感应强度为
方向竖直向下;
[2]直导线M处在直导线N的磁场中,直导线M受到的磁场力是由直导线N产生的磁场对其施加的。
13.(1);(2)
,
【解析】
(1)根据题意,画出粒子在磁场中运动的轨迹,如图所示:
设粒子在磁场中做圆周运动的半径为r,由几何关系有
解得
由洛伦兹力提供向心力有
解得
(2)因为QO与PO的夹角为53°,所以入射速度与电场垂直,也就是带电粒子在电场中做类平抛运动,又因为从N点射出,所以有
又
qE=ma
解得
,
由动能定理有
可得
14.(1);(2)(3)见解析
【解析】
(1)设带电粒子经过电场加速后,从极板CD正中央的小孔射出时的速度大小为v
带电粒子第一次从电场中射出后,在磁场中做匀速圆周运动,运动向改变,由此可知在场中的运动轨迹为四分之三圆,圆心位于D点,半径为
带电粒子在磁场中运动时,洛伦兹力充当向心力,由牛顿运动定律得
解得
(2)带电粒子由A点垂直于电场方向射入电场之后做类平抛运动
若能够射出电场,运动时间
沿电场方向的位移
有
解得
因此带电粒子恰能从C点射出。
带电粒子在磁场中匀速圆周运动周期为
设带电粒子在磁场中偏转运动时间为,有
带电粒子第一次在电场中加速运动时间也为,因此带电粒子从O点运动到C点的总时间
(3)带电粒子第二次离开电场时的速度为
设粒子离开电场时的偏转角度,则
解得;由此可知在磁场中的运动轨迹为四分之三圆。
第二次在磁场中做圆周运动的向心力由洛伦兹力提供,得
解得;
粒子到达CD线上时与C点的距离,带电粒子恰能从D点射入电场。
根据对称性可知,带电粒子第三次离开电场的位置恰好是在B点,速度是v,方向与BC连垂直,然后以C点为圆心,半径d做圆周运动,从CD的中点第三次进入电场,最终刚好返回O点。粒子运动轨迹的示意图如图所示:
粒子从O点出发返回到O的过程中,四次进出电场,三次在磁场中做四分之三的圆周运动。带电粒子运动的总时间
15.(1),方向垂直面向外;(2);(3)
【解析】
(1)根据沿径向进入匀强磁场必沿径向出来的原则,可知A点速度所在的直线与B点速度所在直线的交点就是圆形磁场的圆心,如图所示,设圆形磁场的半径为R
由几何知识可得
粒子在磁场中运行的轨迹与两个速度相切,设粒子运动的轨道半径为r,由几何知识可得
在磁场中运动洛伦兹力提供向心力可得
解得
由已知条件可得
方向垂直面向外。
(2)从B点进入电场之后将速度分解,沿x轴分速度大小为
沿y轴分速度大小
沿y轴方向向下匀速运动,可知任一时刻位置坐标为
沿y轴做初速度为
加速度大小为
可知任一时刻位置坐标
联立可得
(3)运动总时间分三段。第一段时间在磁场中运动,圆心角为可得
第二段时间在第一象限无场区的时间,在第一象限无场区做匀速直线运动,由几何知识可知在无场区发生的位移为8cm,则时间为
第三段时间在电场中的时间,研究电场中沿x轴运动,再次经过y轴所发生的位移为。可列
由方程可得
所以
16.(1);(2);(3)①减小磁感应强度B0的大小;②。
【解析】
(1)对于带电粒子通过速度选择器的过程有:
解得:
由洛伦兹力提供向心力有:
因为:
因此可解得:
(2)设粒子打到A1时,P与A1之间的距离为x1,设粒子打到A2时,P与A2之间的距离为为x2,因为P到A2的距离与A1到A2的距离相等,所以:
因两粒子的电荷量相同,所以由第(1)问结果有:
所以:
(3)①根据洛伦兹力提供向心:
解得:,
由几何关系可知:
可见,为增大d,应减小磁感应强度B0的大小
②因m1-m2、E、e和B均为定值,根据:
可知,d与B0成反比。因此建立坐标系,可画出d随B0变化的图像为一条过原点的直线,其斜率:
k=
所以这两种同位素离子的质量之差:Δm=
选修3-1磁场
章末复习精炼(解析版)
1.2020年爆发了新冠肺炎,该病毒传播能力非常强,因此研究新冠肺炎病毒株的实验室必须是全程都在高度无接触物理防护性条件下操作。武汉病毒研究所是我国防护等级最高的P4实验室,在该实验室中有一种污水流量计,其原理可以简化为如右图所示模型:废液内含有大量正、负离子,从直径为d的圆柱形容器右侧流入,左侧流出。流量值Q等于单位时间通过横截面的液体的体积。空间有垂直纸面向里的磁感应强度为B的匀强磁场,下列说法正确的是( )
A.带电粒子所受洛伦兹力方向是水平向左
B.正、负粒子所受洛伦兹力方向是相同的
C.污水流量计也可以用于测量不带电的液体的流速
D.只需要测量MN两点电压就能够推算废液的流量
2.湖北武当山金殿,以前在雷雨交加时,金殿的屋顶常会出现盆大的火球,来回滚动。雨过天晴时,大殿金光灿灿,像被重新炼洗过一般,这就是人们所说的“雷火炼殿”奇观。近些年为了保护古建筑,在金殿顶部安装了避雷针,此后,雷火炼殿的奇观消失了。假设某次雷雨时,有一团带大量负电荷的乌云经过其正上方时,发生放电现象。下列说法正确的是( )
A.通过避雷针的电流,方向是从云到殿
B.通过避雷针的电流,不受安培力
C.通过避雷针的电流,所受安培力方向偏西
D.通过避雷针的电流,所受安培力方向竖直向下
3.如图所示,两平行金属板水平放置,板长和板间距均为L,两板间接有直流电源,极板间有垂直纸面向外的匀强磁场。一带电微粒从板左端中央位置以速度垂直磁场方向水平进入极板,微粒恰好做匀速直线运动。若保持板不动,让板向下移动0.5L,微粒从原位置以相同速度进入,恰好做匀速圆周运动,则该微粒在极板间做匀速圆周运动的时间为( )
A.
B.
C.
D.
4.如图,在底边长为L的等腰直角三角形MQN区域内,存在方向垂直于纸面向外、磁感应强度大小为B的匀强磁场。一带电粒子(不计重力)以垂直于底边MN的速度v从底边中点P1射入磁场,粒子离开磁场的位置在直角边QN的中点P2。下列结论正确的是(
)
A.粒子带负电
B.粒子在磁场中运动的轨道半径
C.粒子的比荷
D.粒子在磁场中运动的时间
5.如图所示,一根质量为m的金属棒AC用软线悬挂在磁感强度为B的匀强磁场中,通入A→C方向的电流时,悬线张力不为零,欲使悬线张力为零,可以采用的办法是
(
)
A.不改变电流和磁场方向,适当增大电流
B.只改变电流方向,并适当减小电流
C.不改变磁场和电流方向,适当减小磁感强度
D.同时改变磁场方向,并适当减小磁感强度
6.如图所示,在直角三角形ABC内存在垂直纸面向外的匀强磁场,AC
=
d,∠B
=
30°。现垂直AB边射入一群质量均为m、电荷量均为q、速度大小均为v的带正电粒子,已知垂直AC边射出的粒子在磁场中运动的时间均为t,而在磁场中运动的最长时间为
(不计重力和粒子间的相互作用)。下列判断正确的是( )
A.粒子在磁场中做匀速圆周运动的周期为4t
B.该匀强磁场的磁感应强度大小为
C.粒子在进入磁场时速度大小为
D.粒子在磁场中运动的轨迹半径为
7.如图所示,一个边长为l的正六边形的区域内有匀强磁场,匀强磁场的磁感应强度大小为B、方向垂直于纸面向外。在点处的粒子源发出大量质量为电荷量为的同种粒子,粒子的速度大小不同,方向始终沿方向。不计粒子间的相互作用力及重力,下列说法正确的是( )
A.速度小于的粒子在磁场中运动的时间一定相同
B.速度大于的粒子一定打在边上
C.经过点的粒子在磁场中运动的时间为
D.垂直打在边上的粒子在磁场中运动的时间为
8.如图所示,质量均为m的物块a、b用一根劲度系数为k的轻弹簧相连接,放在倾角为θ的足够长光滑固定斜面上,且a是带电量为+q的绝缘物块,b不带电,C为固定挡板.整个装置处于磁感应强度大小为B、方向垂直纸面向里的匀强磁场中,系统处于静止状态.现用一外力F沿斜面方向拉物块a使之向上做匀加速运动,当物块a刚要离开斜面时物块b恰将离开挡板C.重力加速度大小为g,则此过程中
A.物块a运动的距离为
B.b刚要离开挡板时弹簧弹力为2mgsinθ
C.外力F做的功为
D.物块a运动的时间为
9.如图,正方形abcd区域内有垂直纸面的匀强磁场。a点处的粒子源沿ac方向发出大量相同的带电粒子,粒子的速度大小不同。当粒子速度为v0时恰好从e点垂直cd边射出,不计粒子间的相互作用力及重力,下列说法正确的是( )
A.e点为cd边的中点
B.速度为时,粒子从d点射出
C.速度小于的所有粒子在磁场中运动的路程与速度大小成正比
D.从e点射出的粒子和从d点射出的粒子在磁场中运动的时间之比为2:1
10.南极考察队队员在地球南极附近用弹簧秤竖直悬挂一未通电螺线管,如图所示,下列说法正确的是( )
A.若将a端接电源正极,b端接电源负极,则弹簧秤示数将减小
B.若将a端接电源正极,b端接电源负极,则弹簧秤示数将增大
C.若将b端接电源正极,a端接电源负极,则弹簧秤示数将增大
D.不论螺线管通电情况如何,弹簧秤示数均不变
11.如图所示,质量为m、电荷量为q的带电粒子(不计重力),以速度v沿垂直于磁场的方向进入一匀强磁场区域,并在磁场中做匀速圆周运动。已知磁场的磁感应强度为B,则该粒子做匀速圆周运动的轨道半径为____________
,周期为_____________。
12.如图,两根互相平行的长直导线M、N垂直穿过纸面,导线中通有大小相等、方向相反的电流,A、O、B在MN连线上,且将连线四等分。已知直线电流I产生磁场的磁感应强度分布规律是(k为比例系数,为磁场中某点到直导线的距离),现测得O点磁感应强度的大小为3T,则A点的磁感应强度大小为__________T。直导线M受到的磁场力是由_________产生的磁场对其施加的。
13.如图,在纸面内有一圆心为O、半径为R的圆,圆形区域内存在斜向上的电场,电场强度大小未知,区域外存在垂直于纸面向外的匀强磁场,磁感应强度大小为B,一质量为m、电荷量为q的正粒子从圆外P点在纸面内垂直于OP射出,已知粒子从Q点(未画出)进入圆形区域时速度垂直Q点的圆弧切线,随后在圆形区域内运动,并从N点(ON连线的方向与电场方向一致,ON与PO的延长线夹角)射出圆形区域,不计粒子重力,已知OP=3R
(1)求粒子第一次在磁场中运动的速度大小;
(2)求电场强度和粒子射出电场时的速度大小。
14.如图所示,两块平行极板AB、CD正对放置,极板CD的正中央有一小孔,两极板间距离AD为2h,板长AB为4h,两极板间电势差为U,在ABCD构成的矩形区域内存在匀强电场,电场方向水平向右。在ABCD矩形区域外有垂直于纸面向里的范围足够大的匀强磁场。极板厚度不计,电场、磁场的交界处为理想边界。将一个质量为m、电荷量为+q的带电粒子在极板AB的正中央O点由静止释放,带电粒子能够垂直电场方向再次进入匀强电场,带电粒子的重力不计。
(1)求磁场的磁感应强度B的大小;
(2)求出带电粒子从O点开始运动到第二次离开电场区域所经历的总时间;
(3)通过分析说明带电粒子最后能否返回最初的出发点O,若能,请画出粒子运动轨迹的示意图并出带电粒子从O点开始运动到最终返回O点所经历的总时间。若不能,请说明理由。
15.如图所示,竖直平面直角坐标系第一象限有垂直于该竖直面、磁感应强度未知的圆形匀强磁场区域,圆形磁场边界与Y轴上的A(0,cm)点相切;第四象限有充满整个象限水平向左大小的匀强电场。现一质量m=2×10-4kg、带电量为q=+C的微粒从A点以v=4m/s垂直于Y轴沿+X方向射入圆形磁场,经圆形磁场作用后最终从B(10cm,0)点离开第一象限进入第四象限,进入第四象限时速度与X轴正方向成θ=60°(微粒重力不计)。求:
(1)圆形磁场磁感应强度大小及方向;
(2)微粒在第四象限内的轨迹方程(即x关于y的函数);
(3)微粒从A开始运动到再次经过Y轴所经历的时间。
16.如图所示为质谱仪的构造原理图,它是一种分离和检测不同同位素的重要工具。质子数相同而中子数不同的同一元素的不同核素互称为同位素。现让待测的不同带电粒子经加速后进入速度选择器,速度选择器的平行金属板之间有相互正交的匀强磁场和匀强电场(图中未画出),磁感应强度为B,电场强度为E。金属板靠近平板S,在平板S上有可让粒子通过的狭缝P,带电粒子经过速度选择器后,立即从P点沿垂直平板S且垂直于磁场方向的速度进入磁感应强度为B0、并以平板S为边界的有界匀强磁场中,在磁场中偏转后打在记录它的照相底片上,底片厚度可忽略不计,且与平板S重合。根据粒子打在底片上的位置,便可以对它的比荷(电荷量与质量之比)情况进行分析。在下面的讨论中,磁感应强度为B0的匀强磁场区域足够大,空气阻力、带电粒子所受的重力及它们之间的相互作用力均可忽略不计。
(1)若某带电粒子打在底片上的A点,测得P与A之间的距离为x,求该粒子的比荷;
(2)若有两种质量不同的正一价离子,质量分别为m1和m2,它们经速度选择器和匀强磁场后,分别打在底片上的A1和A2两点,测得P到A2的距离与A1到A2的距离相等,求这两种离子的质量之比;
(3)若用这个质谱仪分别观测氢的两种同位素离子(所带电荷量为e),它们分别打在照相底片上相距为d的两点;
①为了便于观测,希望d的数值大一些为宜。试分析说明为了便于观测,应如何改变匀强磁场磁感应强度B0的大小;
②研究小组的同学对上述B0影响d的问题进行了深入的研究。为了直观,他们以d为纵坐标、以为横坐标,画出了d随变化的关系图像,该图像为一条过原点的直线。测得该直线的斜率为k,求这两种同位素离子的质量之差Δm。
参考答案
1.D
【解析】
A.根据左手定则,正电荷受到竖直向下的洛伦兹力,负电荷受到竖直向上的洛伦兹力,AB错误;
C.不带电液体在磁场中流动时,由于没有自由电荷,不能形成电场,MN两点没有电势差,因此无法测出流速,C错误;
D.计算液体的流速,根据
可得流速
流量
D正确。
故选D。
2.C
【解析】
A.电流的方向为正电荷移动的方向与负电荷移动方向相反,大量负电荷从云通过避雷针,说明电流方向是从殿到云,A错误;
BCD.地磁场大致方向是从南到北,根据左手定则,其所受安培力方向偏西,C正确,BD错误。
故选C。
3.A
【解析】
微粒恰好做匀速直线运动时有
恰好做匀速圆周运动
联立解得
即
由题意可知,则有
由公式
得
联立解得
微粒运动轨迹如图所示,由几何关系可得
所以微粒在磁场中运动的时间为
故A正确,BCD错误。
故选A。
4.C
【解析】
A.由题意,可知粒子从P1点进,从P2点出,则粒子向右偏转,根据左手定则可知,粒子带正电,故A错误;
BC.根据题意作出粒子的运动轨迹,如图所示
由题意知,,底边,则根据几何关系可知
,
由题知,为等腰直角三角形,则,在中,根据余弦定理有
解得
粒子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力,则有
解得粒子的比荷,故B错误,C正确;
D.因半径,则由几何关系可得
故,且,所以,故粒子在磁场中偏转的角度也为,则粒子在磁场中运动的时间为
又
解得,故D错误。
故选C。
5.A
【解析】
对导体棒,由平衡知识可知T+F安=mg;若不改变电流和磁场方向,适当增大电流,可增大安培力,能使悬线张力为零.故A正确;只改变电流方向,金属棒所受安培力方向向下,悬线张力一定不为零.故B错误;不改变磁场和电流方向,适当减小磁感应强度,则安培力减小,悬线张力一定不为零.故C错误;同时改变磁场和电流方向,安培力的方向不变,但适当减小磁感应强度会使安培力减小,悬线张力一定不为零.故D错误;故选A.
6.ABD
【解析】
A.带电粒子在磁场中做匀速圆周运动,垂直AC边射出的粒子在磁场中运动的时间是,即
则得周期
选项A正确;
B.由得
故B正确。
D.设运动时间最长的粒子在磁场中的运动轨迹所对的圆心角为,则有
解得
画出该粒子的运动轨迹如图:
设轨道半径为R,由几何知识得
可得
选项D正确;
C.根据线速度的定义有
选项C错误。
故选ABD。
7.ACD
【解析】
A.根据几何关系,粒子恰好经过点时运动半径
由
可知速度
则速度小于的粒子均从边离开磁场,根据几何关系可知转过的圆心角均为,运动时间均为
为粒子在磁场中的运动周期,A正确;
BC.粒子恰好经过点时运动半径
根据几何关系可知运动时间
速度
则速度大于的粒子一定打在边上,B错误,C正确;
D.粒子垂直打在边上时,如图:
根据几何关系可知圆心角为,运动时间
D正确。
故选ACD。
8.AD
【解析】
A.刚开始时,弹簧处于压缩状态,弹簧弹力大小:,物块b恰将离开挡板时,弹簧处于伸长状态,弹簧弹力大小:.整个过程弹簧形变量即a的运动距离,A正确
B.b刚要离开挡板时对b分析有弹簧弹力:,B错误
CD.物块a刚要离开斜面时,垂直于斜面方向有,解得:,物块a匀加速,有,,联立解得:;整个过程的初末状态弹簧的弹性势能大小相等,根据动能定理得:解得:,C错误D正确
9.BC
【解析】
A.当粒子速度为v0时恰好从e点垂直cd边射出时,由几何关系可得
则
所以e点不是cd边的中点,故A错误;
B.由公式
得
速度为时,半径变为
设粒子从d点射出,此时弦长为
则假设成立,故B正确;
C.速度小于的所有粒子均从ad边射出,则粒子的偏转角相同,所以
故C正确;
D.从e点射出的粒子的偏转角为,从d点射出的粒子的弦切角为,则从d点射出的粒子的偏转角为弦切角的两倍,由
可知,从e点射出的粒子和从d点射出的粒子在磁场中运动的时间之比为1:2,故D错误。
故选BC。
10.AC
【解析】
AB.若将端接电源正极,端接电源负极,则根据安培定则可知,螺线管的下端是磁场的N极,磁场的方向向下;又南极附近的磁场的方向向上,所以螺旋管将受到排斥力,弹簧测力计示数将减小,故A正确,B错误;
C.若将端接电源正极,端接电源负极,则根据安培定则可知,螺线管的上端是磁场的N极,磁场的方向向上;又南极附近的磁场的方向向上,所以螺旋管将受到吸引力,弹簧测力计示数将增大,故C正确;
D.由上分析可知,故D错误;
故选AC。
11.
【解析】
[1][2]带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,故有
且有
解得
,
12.4
直导线N
【解析】
[1]设MN的距离为L,根据两通电直导线在O的磁场由右手螺旋定则知均竖直向下,磁感应强度的大小为两同向合成,有
同理A点的磁感应强度为
方向竖直向下;
[2]直导线M处在直导线N的磁场中,直导线M受到的磁场力是由直导线N产生的磁场对其施加的。
13.(1);(2)
,
【解析】
(1)根据题意,画出粒子在磁场中运动的轨迹,如图所示:
设粒子在磁场中做圆周运动的半径为r,由几何关系有
解得
由洛伦兹力提供向心力有
解得
(2)因为QO与PO的夹角为53°,所以入射速度与电场垂直,也就是带电粒子在电场中做类平抛运动,又因为从N点射出,所以有
又
qE=ma
解得
,
由动能定理有
可得
14.(1);(2)(3)见解析
【解析】
(1)设带电粒子经过电场加速后,从极板CD正中央的小孔射出时的速度大小为v
带电粒子第一次从电场中射出后,在磁场中做匀速圆周运动,运动向改变,由此可知在场中的运动轨迹为四分之三圆,圆心位于D点,半径为
带电粒子在磁场中运动时,洛伦兹力充当向心力,由牛顿运动定律得
解得
(2)带电粒子由A点垂直于电场方向射入电场之后做类平抛运动
若能够射出电场,运动时间
沿电场方向的位移
有
解得
因此带电粒子恰能从C点射出。
带电粒子在磁场中匀速圆周运动周期为
设带电粒子在磁场中偏转运动时间为,有
带电粒子第一次在电场中加速运动时间也为,因此带电粒子从O点运动到C点的总时间
(3)带电粒子第二次离开电场时的速度为
设粒子离开电场时的偏转角度,则
解得;由此可知在磁场中的运动轨迹为四分之三圆。
第二次在磁场中做圆周运动的向心力由洛伦兹力提供,得
解得;
粒子到达CD线上时与C点的距离,带电粒子恰能从D点射入电场。
根据对称性可知,带电粒子第三次离开电场的位置恰好是在B点,速度是v,方向与BC连垂直,然后以C点为圆心,半径d做圆周运动,从CD的中点第三次进入电场,最终刚好返回O点。粒子运动轨迹的示意图如图所示:
粒子从O点出发返回到O的过程中,四次进出电场,三次在磁场中做四分之三的圆周运动。带电粒子运动的总时间
15.(1),方向垂直面向外;(2);(3)
【解析】
(1)根据沿径向进入匀强磁场必沿径向出来的原则,可知A点速度所在的直线与B点速度所在直线的交点就是圆形磁场的圆心,如图所示,设圆形磁场的半径为R
由几何知识可得
粒子在磁场中运行的轨迹与两个速度相切,设粒子运动的轨道半径为r,由几何知识可得
在磁场中运动洛伦兹力提供向心力可得
解得
由已知条件可得
方向垂直面向外。
(2)从B点进入电场之后将速度分解,沿x轴分速度大小为
沿y轴分速度大小
沿y轴方向向下匀速运动,可知任一时刻位置坐标为
沿y轴做初速度为
加速度大小为
可知任一时刻位置坐标
联立可得
(3)运动总时间分三段。第一段时间在磁场中运动,圆心角为可得
第二段时间在第一象限无场区的时间,在第一象限无场区做匀速直线运动,由几何知识可知在无场区发生的位移为8cm,则时间为
第三段时间在电场中的时间,研究电场中沿x轴运动,再次经过y轴所发生的位移为。可列
由方程可得
所以
16.(1);(2);(3)①减小磁感应强度B0的大小;②。
【解析】
(1)对于带电粒子通过速度选择器的过程有:
解得:
由洛伦兹力提供向心力有:
因为:
因此可解得:
(2)设粒子打到A1时,P与A1之间的距离为x1,设粒子打到A2时,P与A2之间的距离为为x2,因为P到A2的距离与A1到A2的距离相等,所以:
因两粒子的电荷量相同,所以由第(1)问结果有:
所以:
(3)①根据洛伦兹力提供向心:
解得:,
由几何关系可知:
可见,为增大d,应减小磁感应强度B0的大小
②因m1-m2、E、e和B均为定值,根据:
可知,d与B0成反比。因此建立坐标系,可画出d随B0变化的图像为一条过原点的直线,其斜率:
k=
所以这两种同位素离子的质量之差:Δm=
同课章节目录
