2019—2020学年教科版选修3-1 磁场 章末复习精炼3(解析版)
文档属性
| 名称 | 2019—2020学年教科版选修3-1 磁场 章末复习精炼3(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 581.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-20 00:00:00 | ||
图片预览




文档简介
2019—2020学年教科版
选修3-1磁场
章末复习精炼(解析版)
1.如图所示,三根通电长直导线P、Q、R均垂直纸面放置,ab为直导线P、Q连线的中垂线,P、Q中电流强度的大小相等、方向均垂直纸面向里,R中电流的方向垂直纸面向外,则R受到的磁场力可能是( )
A.F1
B.F2
C.F3
D.F4
2.如图所示,等腰直角三角形OPQ,直角边OP、OQ长度均为L,直角三角形平面内(包括边界)有一垂直平面向外的匀强磁场,磁感应强度大小为B,在PQ边下方放置一带电粒子发射装置,它由P向Q缓慢移动的同时沿垂直PQ边发射出速率都是v的相同正粒子,已知带电粒子的比荷为,粒子的重力、粒子之间的相互作用力不计。则粒子在磁场中运动的最长时间为( )
A.
B.
C.
D.
3.如图所示,条形磁铁放在水平桌面上,在其上方正中央固定一根长直导线,导线与磁铁垂直。导线通以垂直纸面向里的电流,则通电后( )
A.磁铁对桌面压力减小,不受桌面的摩擦力作用
B.磁铁对桌面压力减小,受到桌面的摩擦力作用
C.磁铁对桌面压力增加,不受桌面的摩擦力作用
D.磁铁对桌面压力增加,受到桌面的摩擦力作用
4.用DIS的磁传感器可以测定通电螺线管内的磁感应强度,当磁传感器的探测头从螺线管左端外侧逐渐伸入螺线管,直到伸出右端为止。测出的B-x图是( )
A.B.C.D.
5.如图所示,边长为L的等边三角形ABC内、外分布着两方向相反的匀强磁场,三角形内磁场方向垂直纸面向外,两磁场的磁感应强度大小均为B。顶点A处有一粒子源,粒子源能沿∠BAC的角平分线发射不同速率的粒子,粒子质量均为m、电荷量均为+q,不计粒子重力及粒子间的相互作用力,则发射速度v0为哪一值时粒子能通过B点( )
A.
B.
C.
D.
6.三条在同一平面(纸面)内的长直绝缘导线组成一等边三角形,在导线中通过的电流均为I,方向如图所示。a、b和c三点分别位于三角形的三个顶角的角平分线上,且到相应顶点的距离相等。将a、b和c处的磁感应强度大小分别记为B1、B2和B3,下列说法正确的是( )
A.B1=B2B.B1=B2=B3
C.a和c处磁场方向垂直于纸面向外,b处磁场方向垂直于纸面向里
D.a处磁场方向垂直于纸面向外,b和c处磁场方向垂直于纸面向里
7.如图,有一个带有小缺口的绝缘圆环内存在垂直纸面向外的匀强磁场,圆环绕圆心逆时针转动。一带正电的粒子从小缺口沿直径方向进入圆环内部,且与圆环没有发生碰撞,最后从小缺口处离开磁场区域。已知粒子的比荷为k,磁场的磁感应强度大小为B,圆环的半径为R,粒子进入磁场时的速度为,不计粒子的重力。则圆环旋转的的角速度可能为( )
A.2kB
B.3kB
C.5kB
D.7kB
8.如图所示,质量为m,带电荷量为q的微粒以速度v与水平方向成45°角进入匀强电场和匀强磁场,磁场方向垂直纸面向里。如果微粒做匀速直线运动,则下列说法正确的是( )
A.微粒受电场力、洛伦兹力、重力三个力作用
B.微粒带负电,微粒在运动中电势能不断增加
C.匀强电场的电场强度
D.匀强磁场的磁感应强度
9.如图所示,等腰直角三角形abc区域内存在方向垂直纸面向外的匀强磁场,磁感应强度大小为B。三个相同的带电粒子从b点沿bc方向分别以速度v1、v2、v3射入磁场,在磁场中运动的时间分别为t1、t2、t3,且t1:t2:t3=3:3:1。直角边bc的长度为L,不计粒子的重力,下列说法正确的是
A.三个粒子的速度大小关系可能是v1=v2>v3
B.三个粒子的速度大小关系可能是v1C.粒子的比荷
D.粒子的比荷
10.如图所示,一块长度为a、宽度为b、厚度为d的金属导体,当加有与前后表面垂直的匀强磁场B,且通以图示方向的电流I时,用电压表测得导体上、下表面MN间电压为U。已知自由电子的电量为e。下列说法中正确的是( )
A.M板比N板电势高
B.导体中自由电子定向移动的速度为
C.仅将磁场方向变为与导体的的左右表面垂直时,U不变
D.导体单位体积内的自由电子数为
11.如图所示的平行板器件中,电场强度E和磁感应强度B相互垂直,具有不同水平速度的带电粒子射入后发生偏转的情况不同。若从左侧水平射入的带电粒子,不计重力,穿过这一区域时未发生偏转,则该粒子的速度大小为________;若只改变该粒子的电性,则粒子穿过这一区域时是否会发生偏转?________(选填“会”或“不会”)。
12.如图所示,正方形线圈abcd位于纸面内,边长为L,匝数为N,过ab中点和cd中点的连线OO′恰好位于垂直纸面向里的匀强磁场的右边界上,磁感应强度为B,则穿过线圈的磁通量为______________
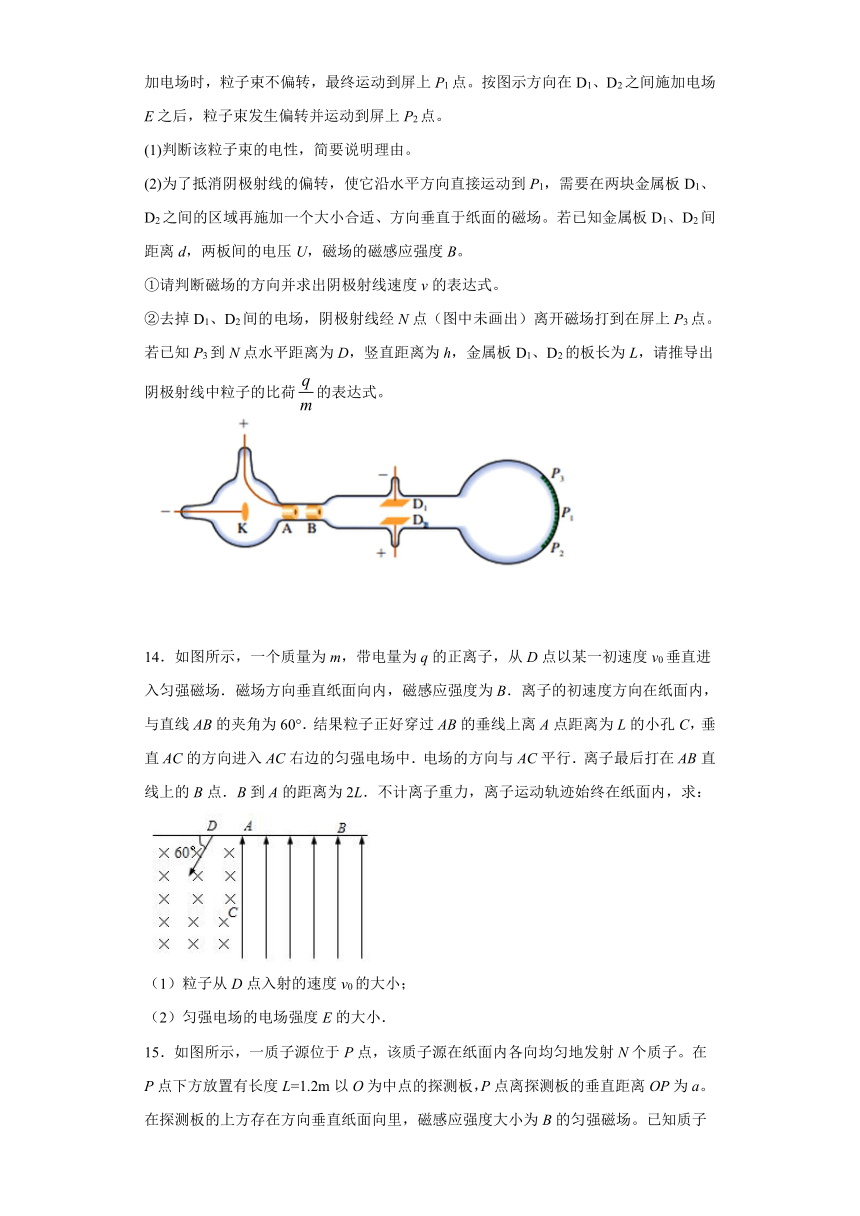
13.物理学中将带电粒子的电荷量与其质量之比称为比荷,根据某带电粒子在电场和磁场中受力及运动情况,可以得出它的比荷。如图是阴极射线管,左端正负极接高压电源可从阴极K水平向右发射带电粒子束(也叫阴极射线),当图中金属板D1、D2之间未加电场时,粒子束不偏转,最终运动到屏上P1点。按图示方向在D1、D2之间施加电场E之后,粒子束发生偏转并运动到屏上P2点。
(1)判断该粒子束的电性,简要说明理由。
(2)为了抵消阴极射线的偏转,使它沿水平方向直接运动到P1,需要在两块金属板D1、D2之间的区域再施加一个大小合适、方向垂直于纸面的磁场。若已知金属板D1、D2间距离d,两板间的电压U,磁场的磁感应强度B。
①请判断磁场的方向并求出阴极射线速度v的表达式。
②去掉D1、D2间的电场,阴极射线经N点(图中未画出)离开磁场打到在屏上P3点。若已知P3到N点水平距离为D,竖直距离为h,金属板D1、D2的板长为L,请推导出阴极射线中粒子的比荷的表达式。
14.如图所示,一个质量为m,带电量为q的正离子,从D点以某一初速度v0垂直进入匀强磁场.磁场方向垂直纸面向内,磁感应强度为B.离子的初速度方向在纸面内,与直线AB的夹角为60°.结果粒子正好穿过AB的垂线上离A点距离为L的小孔C,垂直AC的方向进入AC右边的匀强电场中.电场的方向与AC平行.离子最后打在AB直线上的B点.B到A的距离为2L.不计离子重力,离子运动轨迹始终在纸面内,求:
(1)粒子从D点入射的速度v0的大小;
(2)匀强电场的电场强度E的大小.
15.如图所示,一质子源位于P点,该质子源在纸面内各向均匀地发射N个质子。在P点下方放置有长度L=1.2m以O为中点的探测板,P点离探测板的垂直距离OP为a。在探测板的上方存在方向垂直纸面向里,磁感应强度大小为B的匀强磁场。已知质子电荷量q=1.60×10?19C,质子的质量与速度的乘积mv=4.8×10-21kg·m·s?1(不考虑粒子之间的相互作用)。求
(1)当a=0.15m,B=0.1T时,求计数率(即打到探测板上质子数与总质子数N的比值);
(2)若a取不同的值,可通过调节B的大小获得与(1)问中同样的计数率,求B与a的关系并给出B的取值范围。
16.如图所示,金属杆垂直放置于间距为L的水平平行金属导轨上,并处于竖直向上,磁感线强度为B的匀强磁场中,已知电阻电动势为E,内阻为r,金属杆连入电路的电阻为R,其他电阻均不计。则闭合开关瞬间:
(1)细杆所受安培力水平向左还是水平向右?
(2)电路中电流I多大?
(3)细杆所受安培力F多大?
参考答案
1.C
【解析】
根据异向电流相斥,同向电流相吸可知,电流PQ对电流R均产生吸引力,但是由于P距离R较近,Q距离R较远,则P对R的斥力大于Q对R的斥力,则根据平行四边形法则合成可知,合力方向可能为F3的方向。
故选C。
2.D
【解析】
根据
代入数据,可知带电粒子在磁场中运动的轨道半径
根据左手定则可知,粒子恰好与PO边相切时运动时间最长,如图所示
根据对称性可知,运动轨迹也恰好与OQ相切,恰好运动了半径圆周,因此运动的最长时间为
D正确,ABC错误。
故选D。
3.C
【解析】
画出条形磁铁的磁场,通电后受力分析如图
通电后,磁铁对导线的安培力竖直向上,根据牛顿第三定律可知导线对磁铁的安培力竖直向下,相比未通电时磁铁对桌面压力增加,磁铁不受摩擦力,ABD错误,C正确。
故选C。
4.C
【解析】
通电螺线管的磁场分布相当于条形磁铁,内部磁感线的分布均匀,是匀强磁场,管口磁感线比管内磁感线疏,故管口处的磁感应强度较小,故C正确,ABD错误。
故选C。
5.D
【解析】
粒子带正电,且经过B点,其可能的轨迹如图所示
所有圆弧所对圆心角均为60°,所以粒子运行半径
r=(n=1,2,3,…)
粒子在磁场中做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得
qvB=m
解得
(n=1,2,3,…)
由此可知,的粒子能通过B点,故ABC不符合题意,D符合题意。
故选D。
6.A
【解析】
AB.由安培定则判断,对a和b,其临近的两条导线在a和b点产生的磁感应强度等大方向,磁感应强度相互抵消,则a和b处的磁感应强度就等于远离的那条导线产生的磁感应强度,有;对c,其临近的两条导线在c产生的磁感应强度等大同向,磁感应强度加倍,而远离c的那条导线在c产生的磁感应强度小于其临近的两条导线在c产生的磁感应强度,且方向相反,在c处的磁感应强度应大于a和b处的磁感应强度和,
A正确,B错误;
CD.由安培定则判断可得a和b处磁场方向垂直于纸面向外,c处磁场方向垂直于纸面向里,CD错误;
故选A.
7.C
【解析】
ABCD.带电粒子在磁场中做圆周运动的半径为r,由洛伦兹力提供向心力
可得
如图所示,该带电粒子将从圆的最低点离开磁场,所用时间
要使得带电粒子能从圆环缺口离开磁场,则环绕圆心逆时针转动的角速度满足
当时
,,,...
ABD错误,C正确;
故选C.
8.AB
【解析】
AB.若微粒带正电,电场力水平向左,洛伦兹力垂直速度方向斜向下,而重力竖直向下,则三个力不可能平衡,可知微粒带负电,受力如图所示
由于粒子带负电,电场力向右,洛伦兹力垂直于速度方向斜向左上方,而重力竖直向下,则电场力、洛伦兹力和重力能平衡,致使粒子做匀速直线运动,电场力做负功,则电势能不断增加,故A、B正确;
CD.根据平衡有
解得
故C、D错误;
故选AB。
9.BD
【解析】速度为的粒子从ab边穿出,则偏转角为90°,但两者的速度大小关系不定,但其半径一定比速度为的粒子半径小,由半径公式,则一定大于和,
A错误B正确;对速度为的粒子偏转30°,画出运动轨迹如图所示,由几何关系知,所以,而,联立得到,C错误;由于速度为的粒子偏转90°,则,于是,D正确.
【点睛】此题涉及的是带电粒子在三角形磁场区域内做匀速圆周运动问题,要注意的是已知的是带电粒子在磁场区域内的时间之比,也就是告诉了偏转角之比,结合题意就知道带电粒子从哪条边穿出,从而知道偏转角的大小,由几何关系也能求出粒子3的半径,由半径和周期公式就能求出速度大小关系和比荷.
10.BD
【解析】
A.如图,电流方向向右,电子向左移动,根据左手定则判断可知,电子所受的洛伦兹力方向向上,则M积累了电子,MN之间产生向上的电场,因此M板比N板电势低,故A错误;
B.由
变形可得自由电子定向移动速度为
故B正确;
C.如果把磁场方向变为与导体的左右表面垂直的话,电子所受的洛伦兹力为零,无法到达上下表面,则U为零,故C错误;
D.电流的微观表达式为
则导体单位体积内的自由电子数为
又因为
联立解得
故D正确。
故选BD。
11.
不会
【解析】带电粒子未发生偏转则,所以,只改变该粒子的电性,粒子所受的电场力和洛伦兹力方向改变,但大小不变以,所以不会发生偏转
12.
;
【解析】
当正方形线圈abcd有一半处在磁感应强度为B的匀强磁场中时,磁通量为:
【点睛】
在匀强磁场中,当线圈与磁场垂直时,穿过线圈的磁通量为,S有磁感线穿过线圈的面积,即为有效面积,磁通量与线圈的匝数无关。
13.(1)负电荷;(2)①v=,②
【解析】
(1)粒子束经过电场时受到向下的场力偏转,场强方向向上,场强方向与电场力方向相反,所以粒子带负电荷。
(2)①磁场力方向与电场力方向相反,由左手定则可判断出磁场方向垂直纸面向外,由题意可得出当电场力大小等于磁场力,粒子束所受合力为零,做匀速直线运动,有
联立解得速度的表达式为
②粒子进入磁场中,在洛仑兹力的作用下做匀速圆周运动,离开磁场后做匀速直线运动,如下图所示
由牛顿第二定律
又
解得
14.(1);(2).
【解析】
(1)离子在磁场中做圆周运动,轨迹如图所示.
由几何关系可知,离子圆周运动半径r满足:
①
离子在磁场中做圆周运动,洛伦兹力提供向心力
由牛顿第二定律:
②
由①②解得入射速度
③
(2)离子进入电场后做类平抛运动,轨迹如图所示.
水平方向
④
竖直方向
⑤
由③④⑤解得匀强电场的电场强度
⑥
15.(1);(2)
,
【解析】
(1)
根据牛顿第二定律,有,得质子运动半径:
如图所示
轨迹与AB相切时落点最远,设质子与竖直方向的发射角为α时在O点左侧相切,发射角为β时在O点右侧相切,根据几何关系知,打到探测板对应发射角度:
能够打在AB板的夹角为:
可得质子计数率为:
(2)
在确保计数率为的情况下,R'=2a,即,如图所示
恰能打到探测板左端的条件为
即
16.(1)水平向右;(2);(3)
【解析】
(1)由左手定则可知,安培力方向:水平向右
(2)由闭合电路欧姆定律可知,闭合开关瞬间电流
(3)细杆所受安培力大小
选修3-1磁场
章末复习精炼(解析版)
1.如图所示,三根通电长直导线P、Q、R均垂直纸面放置,ab为直导线P、Q连线的中垂线,P、Q中电流强度的大小相等、方向均垂直纸面向里,R中电流的方向垂直纸面向外,则R受到的磁场力可能是( )
A.F1
B.F2
C.F3
D.F4
2.如图所示,等腰直角三角形OPQ,直角边OP、OQ长度均为L,直角三角形平面内(包括边界)有一垂直平面向外的匀强磁场,磁感应强度大小为B,在PQ边下方放置一带电粒子发射装置,它由P向Q缓慢移动的同时沿垂直PQ边发射出速率都是v的相同正粒子,已知带电粒子的比荷为,粒子的重力、粒子之间的相互作用力不计。则粒子在磁场中运动的最长时间为( )
A.
B.
C.
D.
3.如图所示,条形磁铁放在水平桌面上,在其上方正中央固定一根长直导线,导线与磁铁垂直。导线通以垂直纸面向里的电流,则通电后( )
A.磁铁对桌面压力减小,不受桌面的摩擦力作用
B.磁铁对桌面压力减小,受到桌面的摩擦力作用
C.磁铁对桌面压力增加,不受桌面的摩擦力作用
D.磁铁对桌面压力增加,受到桌面的摩擦力作用
4.用DIS的磁传感器可以测定通电螺线管内的磁感应强度,当磁传感器的探测头从螺线管左端外侧逐渐伸入螺线管,直到伸出右端为止。测出的B-x图是( )
A.B.C.D.
5.如图所示,边长为L的等边三角形ABC内、外分布着两方向相反的匀强磁场,三角形内磁场方向垂直纸面向外,两磁场的磁感应强度大小均为B。顶点A处有一粒子源,粒子源能沿∠BAC的角平分线发射不同速率的粒子,粒子质量均为m、电荷量均为+q,不计粒子重力及粒子间的相互作用力,则发射速度v0为哪一值时粒子能通过B点( )
A.
B.
C.
D.
6.三条在同一平面(纸面)内的长直绝缘导线组成一等边三角形,在导线中通过的电流均为I,方向如图所示。a、b和c三点分别位于三角形的三个顶角的角平分线上,且到相应顶点的距离相等。将a、b和c处的磁感应强度大小分别记为B1、B2和B3,下列说法正确的是( )
A.B1=B2
C.a和c处磁场方向垂直于纸面向外,b处磁场方向垂直于纸面向里
D.a处磁场方向垂直于纸面向外,b和c处磁场方向垂直于纸面向里
7.如图,有一个带有小缺口的绝缘圆环内存在垂直纸面向外的匀强磁场,圆环绕圆心逆时针转动。一带正电的粒子从小缺口沿直径方向进入圆环内部,且与圆环没有发生碰撞,最后从小缺口处离开磁场区域。已知粒子的比荷为k,磁场的磁感应强度大小为B,圆环的半径为R,粒子进入磁场时的速度为,不计粒子的重力。则圆环旋转的的角速度可能为( )
A.2kB
B.3kB
C.5kB
D.7kB
8.如图所示,质量为m,带电荷量为q的微粒以速度v与水平方向成45°角进入匀强电场和匀强磁场,磁场方向垂直纸面向里。如果微粒做匀速直线运动,则下列说法正确的是( )
A.微粒受电场力、洛伦兹力、重力三个力作用
B.微粒带负电,微粒在运动中电势能不断增加
C.匀强电场的电场强度
D.匀强磁场的磁感应强度
9.如图所示,等腰直角三角形abc区域内存在方向垂直纸面向外的匀强磁场,磁感应强度大小为B。三个相同的带电粒子从b点沿bc方向分别以速度v1、v2、v3射入磁场,在磁场中运动的时间分别为t1、t2、t3,且t1:t2:t3=3:3:1。直角边bc的长度为L,不计粒子的重力,下列说法正确的是
A.三个粒子的速度大小关系可能是v1=v2>v3
B.三个粒子的速度大小关系可能是v1
D.粒子的比荷
10.如图所示,一块长度为a、宽度为b、厚度为d的金属导体,当加有与前后表面垂直的匀强磁场B,且通以图示方向的电流I时,用电压表测得导体上、下表面MN间电压为U。已知自由电子的电量为e。下列说法中正确的是( )
A.M板比N板电势高
B.导体中自由电子定向移动的速度为
C.仅将磁场方向变为与导体的的左右表面垂直时,U不变
D.导体单位体积内的自由电子数为
11.如图所示的平行板器件中,电场强度E和磁感应强度B相互垂直,具有不同水平速度的带电粒子射入后发生偏转的情况不同。若从左侧水平射入的带电粒子,不计重力,穿过这一区域时未发生偏转,则该粒子的速度大小为________;若只改变该粒子的电性,则粒子穿过这一区域时是否会发生偏转?________(选填“会”或“不会”)。
12.如图所示,正方形线圈abcd位于纸面内,边长为L,匝数为N,过ab中点和cd中点的连线OO′恰好位于垂直纸面向里的匀强磁场的右边界上,磁感应强度为B,则穿过线圈的磁通量为______________
13.物理学中将带电粒子的电荷量与其质量之比称为比荷,根据某带电粒子在电场和磁场中受力及运动情况,可以得出它的比荷。如图是阴极射线管,左端正负极接高压电源可从阴极K水平向右发射带电粒子束(也叫阴极射线),当图中金属板D1、D2之间未加电场时,粒子束不偏转,最终运动到屏上P1点。按图示方向在D1、D2之间施加电场E之后,粒子束发生偏转并运动到屏上P2点。
(1)判断该粒子束的电性,简要说明理由。
(2)为了抵消阴极射线的偏转,使它沿水平方向直接运动到P1,需要在两块金属板D1、D2之间的区域再施加一个大小合适、方向垂直于纸面的磁场。若已知金属板D1、D2间距离d,两板间的电压U,磁场的磁感应强度B。
①请判断磁场的方向并求出阴极射线速度v的表达式。
②去掉D1、D2间的电场,阴极射线经N点(图中未画出)离开磁场打到在屏上P3点。若已知P3到N点水平距离为D,竖直距离为h,金属板D1、D2的板长为L,请推导出阴极射线中粒子的比荷的表达式。
14.如图所示,一个质量为m,带电量为q的正离子,从D点以某一初速度v0垂直进入匀强磁场.磁场方向垂直纸面向内,磁感应强度为B.离子的初速度方向在纸面内,与直线AB的夹角为60°.结果粒子正好穿过AB的垂线上离A点距离为L的小孔C,垂直AC的方向进入AC右边的匀强电场中.电场的方向与AC平行.离子最后打在AB直线上的B点.B到A的距离为2L.不计离子重力,离子运动轨迹始终在纸面内,求:
(1)粒子从D点入射的速度v0的大小;
(2)匀强电场的电场强度E的大小.
15.如图所示,一质子源位于P点,该质子源在纸面内各向均匀地发射N个质子。在P点下方放置有长度L=1.2m以O为中点的探测板,P点离探测板的垂直距离OP为a。在探测板的上方存在方向垂直纸面向里,磁感应强度大小为B的匀强磁场。已知质子电荷量q=1.60×10?19C,质子的质量与速度的乘积mv=4.8×10-21kg·m·s?1(不考虑粒子之间的相互作用)。求
(1)当a=0.15m,B=0.1T时,求计数率(即打到探测板上质子数与总质子数N的比值);
(2)若a取不同的值,可通过调节B的大小获得与(1)问中同样的计数率,求B与a的关系并给出B的取值范围。
16.如图所示,金属杆垂直放置于间距为L的水平平行金属导轨上,并处于竖直向上,磁感线强度为B的匀强磁场中,已知电阻电动势为E,内阻为r,金属杆连入电路的电阻为R,其他电阻均不计。则闭合开关瞬间:
(1)细杆所受安培力水平向左还是水平向右?
(2)电路中电流I多大?
(3)细杆所受安培力F多大?
参考答案
1.C
【解析】
根据异向电流相斥,同向电流相吸可知,电流PQ对电流R均产生吸引力,但是由于P距离R较近,Q距离R较远,则P对R的斥力大于Q对R的斥力,则根据平行四边形法则合成可知,合力方向可能为F3的方向。
故选C。
2.D
【解析】
根据
代入数据,可知带电粒子在磁场中运动的轨道半径
根据左手定则可知,粒子恰好与PO边相切时运动时间最长,如图所示
根据对称性可知,运动轨迹也恰好与OQ相切,恰好运动了半径圆周,因此运动的最长时间为
D正确,ABC错误。
故选D。
3.C
【解析】
画出条形磁铁的磁场,通电后受力分析如图
通电后,磁铁对导线的安培力竖直向上,根据牛顿第三定律可知导线对磁铁的安培力竖直向下,相比未通电时磁铁对桌面压力增加,磁铁不受摩擦力,ABD错误,C正确。
故选C。
4.C
【解析】
通电螺线管的磁场分布相当于条形磁铁,内部磁感线的分布均匀,是匀强磁场,管口磁感线比管内磁感线疏,故管口处的磁感应强度较小,故C正确,ABD错误。
故选C。
5.D
【解析】
粒子带正电,且经过B点,其可能的轨迹如图所示
所有圆弧所对圆心角均为60°,所以粒子运行半径
r=(n=1,2,3,…)
粒子在磁场中做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得
qvB=m
解得
(n=1,2,3,…)
由此可知,的粒子能通过B点,故ABC不符合题意,D符合题意。
故选D。
6.A
【解析】
AB.由安培定则判断,对a和b,其临近的两条导线在a和b点产生的磁感应强度等大方向,磁感应强度相互抵消,则a和b处的磁感应强度就等于远离的那条导线产生的磁感应强度,有;对c,其临近的两条导线在c产生的磁感应强度等大同向,磁感应强度加倍,而远离c的那条导线在c产生的磁感应强度小于其临近的两条导线在c产生的磁感应强度,且方向相反,在c处的磁感应强度应大于a和b处的磁感应强度和,
A正确,B错误;
CD.由安培定则判断可得a和b处磁场方向垂直于纸面向外,c处磁场方向垂直于纸面向里,CD错误;
故选A.
7.C
【解析】
ABCD.带电粒子在磁场中做圆周运动的半径为r,由洛伦兹力提供向心力
可得
如图所示,该带电粒子将从圆的最低点离开磁场,所用时间
要使得带电粒子能从圆环缺口离开磁场,则环绕圆心逆时针转动的角速度满足
当时
,,,...
ABD错误,C正确;
故选C.
8.AB
【解析】
AB.若微粒带正电,电场力水平向左,洛伦兹力垂直速度方向斜向下,而重力竖直向下,则三个力不可能平衡,可知微粒带负电,受力如图所示
由于粒子带负电,电场力向右,洛伦兹力垂直于速度方向斜向左上方,而重力竖直向下,则电场力、洛伦兹力和重力能平衡,致使粒子做匀速直线运动,电场力做负功,则电势能不断增加,故A、B正确;
CD.根据平衡有
解得
故C、D错误;
故选AB。
9.BD
【解析】速度为的粒子从ab边穿出,则偏转角为90°,但两者的速度大小关系不定,但其半径一定比速度为的粒子半径小,由半径公式,则一定大于和,
A错误B正确;对速度为的粒子偏转30°,画出运动轨迹如图所示,由几何关系知,所以,而,联立得到,C错误;由于速度为的粒子偏转90°,则,于是,D正确.
【点睛】此题涉及的是带电粒子在三角形磁场区域内做匀速圆周运动问题,要注意的是已知的是带电粒子在磁场区域内的时间之比,也就是告诉了偏转角之比,结合题意就知道带电粒子从哪条边穿出,从而知道偏转角的大小,由几何关系也能求出粒子3的半径,由半径和周期公式就能求出速度大小关系和比荷.
10.BD
【解析】
A.如图,电流方向向右,电子向左移动,根据左手定则判断可知,电子所受的洛伦兹力方向向上,则M积累了电子,MN之间产生向上的电场,因此M板比N板电势低,故A错误;
B.由
变形可得自由电子定向移动速度为
故B正确;
C.如果把磁场方向变为与导体的左右表面垂直的话,电子所受的洛伦兹力为零,无法到达上下表面,则U为零,故C错误;
D.电流的微观表达式为
则导体单位体积内的自由电子数为
又因为
联立解得
故D正确。
故选BD。
11.
不会
【解析】带电粒子未发生偏转则,所以,只改变该粒子的电性,粒子所受的电场力和洛伦兹力方向改变,但大小不变以,所以不会发生偏转
12.
;
【解析】
当正方形线圈abcd有一半处在磁感应强度为B的匀强磁场中时,磁通量为:
【点睛】
在匀强磁场中,当线圈与磁场垂直时,穿过线圈的磁通量为,S有磁感线穿过线圈的面积,即为有效面积,磁通量与线圈的匝数无关。
13.(1)负电荷;(2)①v=,②
【解析】
(1)粒子束经过电场时受到向下的场力偏转,场强方向向上,场强方向与电场力方向相反,所以粒子带负电荷。
(2)①磁场力方向与电场力方向相反,由左手定则可判断出磁场方向垂直纸面向外,由题意可得出当电场力大小等于磁场力,粒子束所受合力为零,做匀速直线运动,有
联立解得速度的表达式为
②粒子进入磁场中,在洛仑兹力的作用下做匀速圆周运动,离开磁场后做匀速直线运动,如下图所示
由牛顿第二定律
又
解得
14.(1);(2).
【解析】
(1)离子在磁场中做圆周运动,轨迹如图所示.
由几何关系可知,离子圆周运动半径r满足:
①
离子在磁场中做圆周运动,洛伦兹力提供向心力
由牛顿第二定律:
②
由①②解得入射速度
③
(2)离子进入电场后做类平抛运动,轨迹如图所示.
水平方向
④
竖直方向
⑤
由③④⑤解得匀强电场的电场强度
⑥
15.(1);(2)
,
【解析】
(1)
根据牛顿第二定律,有,得质子运动半径:
如图所示
轨迹与AB相切时落点最远,设质子与竖直方向的发射角为α时在O点左侧相切,发射角为β时在O点右侧相切,根据几何关系知,打到探测板对应发射角度:
能够打在AB板的夹角为:
可得质子计数率为:
(2)
在确保计数率为的情况下,R'=2a,即,如图所示
恰能打到探测板左端的条件为
即
16.(1)水平向右;(2);(3)
【解析】
(1)由左手定则可知,安培力方向:水平向右
(2)由闭合电路欧姆定律可知,闭合开关瞬间电流
(3)细杆所受安培力大小
同课章节目录
