2019-2020年秋湘教版九年级数学第1章单元《反比例函数》测试题(无答案)
文档属性
| 名称 | 2019-2020年秋湘教版九年级数学第1章单元《反比例函数》测试题(无答案) | 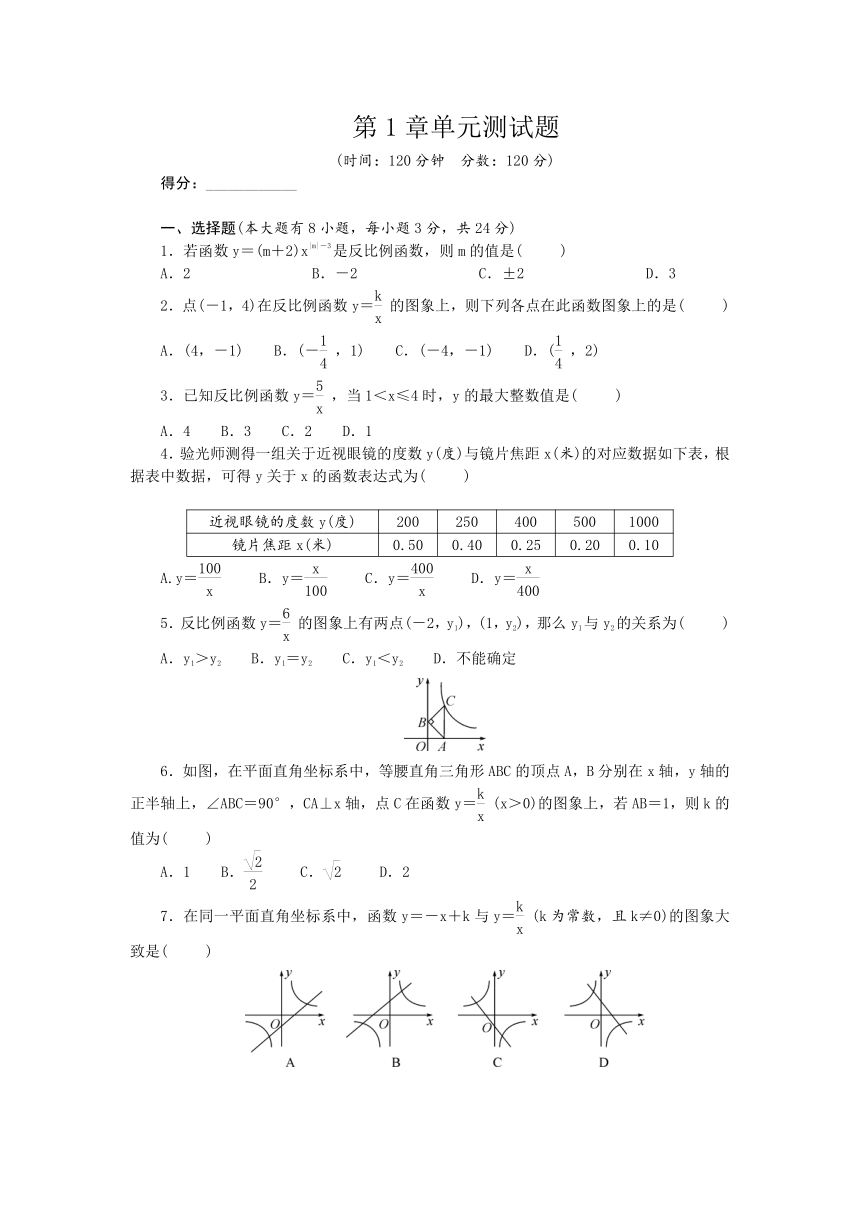 | |
| 格式 | zip | ||
| 文件大小 | 85.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-20 21:51:22 | ||
图片预览


文档简介
第1章单元测试题
(时间:120分钟 分数:120分)
得分:____________
一、选择题(本大题有8小题,每小题3分,共24分)
1.若函数y=(m+2)x|m|-3是反比例函数,则m的值是(
)
A.2 B.-2 C.±2 D.3
2.点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是(
)
A.(4,-1)
B.(-,1)
C.(-4,-1)
D.(,2)
3.已知反比例函数y=,当1<x≤4时,y的最大整数值是(
)
A.4
B.3
C.2
D.1
4.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表,根据表中数据,可得y关于x的函数表达式为(
)
近视眼镜的度数y(度)
200
250
400
500
1000
镜片焦距x(米)
0.50
0.40
0.25
0.20
0.10
A.y=
B.y=
C.y=
D.y=
5.反比例函数y=的图象上有两点(-2,y1),(1,y2),那么y1与y2的关系为(
)
A.y1>y2
B.y1=y2
C.y1<y2
D.不能确定
6.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴,y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=(x>0)的图象上,若AB=1,则k的值为(
)
A.1
B.
C.
D.2
7.在同一平面直角坐标系中,函数y=-x+k与y=(k为常数,且k≠0)的图象大致是(
)
8.如图,在平面直角坐标系中,Rt△ABC的顶点A,C坐标分别是(0,3),(3,0).∠ACB=90°,AC=2BC,则函数y=(k>0,x>0)的图象经过点B,则k的值为(
)
A.
B.9
C.
D.
二、填空题(本大题有8小题,每小题3分,共24分)
9.下列函数是反比例函数的有________.(只填序号)
①y=-,②y=5x-1,③y=(k为常数且k≠0),④y=.
10.双曲线y=在每个象限内,函数值y随x的增大而增大,则m的取值范围是________.
11.如图所示,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C,D在x轴上,且BC∥AD,四边形ABCD的面积为3,则这个反比例函数的表达式为________.
eq
\o(\s\up7(),\s\do5((第11题图)))
eq
\o(\s\up7(),\s\do5((第14题图)))
eq
\o(\s\up7(),\s\do5((第15题图)))
eq
\o(\s\up7(),\s\do5((第16题图)))
12.已知一个函数的图象与y=的图象关于y轴对称,则该函数的解析式为________.
13.根据某商场对一款运动鞋五天中的售价与销量关系的调查显示,售价是销量的反比例函数(统计数据见下表).已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为________元.
售价x(元/双)
200
240
250
400
销售量y(双)
30
25
24
15
14.如图,在平面直角坐标系中,点A的坐标为(-4,2),反比例函数y=(x<0)的图象经过线段OA的中点B,则k=________.
15.如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=(x>0)的图象上,顶点B在函数y2=(x>0)的图象上,∠ABO=30°,则=________.
16.如图,双曲线y=(x>0)经过矩形OABC的顶点B,双曲线y=(x>0)交AB,BC于点E,F,且与矩形的对角线OB交于点D,连接EF.若OD∶OB=2∶3,则△BEF的面积为________.
三、解答题(本大题有9小题,共72分)
17.(6分)已知反比例函数y=(k≠0)的图象经过点A(-3,-6).
(1)求这个函数的表达式;
(2)点B(4,),C(2,-5)是否在这个函数的图象上?
18.(6分)已知反比例函数y=mx|m-2|-4的图象位于第二、四象限.
(1)求m的值;
(2)若点A(x1,y1),B(x2,y2)是反比例函数图象上两点,且x1<0<x2,试比较y1,y2的大小.
19.(6分)某地建设一项水利工程,工程需要运送的土石方总量为360万立方米.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万立方米)之间的函数关系式;
(2)为了能在150天内完成任务,平均每天的工作量至少是多少万立方米?
20.(6分)如图,一次函数y1=x+1的图象与反比例函数y2=(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1.
(1)在第一象限内,当x取何值时,y1>y2?
(2)求反比例函数的表达式.
21.(7分)如图,直线y=x+b与双曲线y=(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
22.(9分)如图,在平面直角坐标系xOy中,函数y=(x>0)的图象与直线y=x-2交于点A(3,m).
(1)求k,m的值;
(2)已知点P(n,n)(n>0),过点P作平行于x轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数y=(x>0)的图象于点N.当n=1时,判断线段PM与PN的数量关系,并说明理由.
23.(10分)如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与y轴交于点C,与反比例函数y=(k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
(1)求反比例函数和一次函数的解析式;
(2)连接OB,MC,求四边形MBOC的面积.
24.(10分)如图,在平面直角坐标系xOy中,点A(3,2)在反比例函数y=(x>0)的图象上,点B在OA的延长线上,BC⊥x轴,垂足为C,BC与反比例函数的图象相交于点D,连接AC,AD.
(1)求该反比例函数的解析式;
(2)若S△ACD=,设点C的坐标为(a,0),求线段BD的长.
25.(12分)为预防疾病,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.根据以上信息,解答下列问题:
(1)求药物燃烧时y与x的函数关系式;
(2)求药物燃烧后y与x的函数关系式;
(3)当每立方米空气中含药量低于1.6mg时,对人体无毒害作用.那么从消毒开始,经过多长时间学生才可以返回教室?
(时间:120分钟 分数:120分)
得分:____________
一、选择题(本大题有8小题,每小题3分,共24分)
1.若函数y=(m+2)x|m|-3是反比例函数,则m的值是(
)
A.2 B.-2 C.±2 D.3
2.点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是(
)
A.(4,-1)
B.(-,1)
C.(-4,-1)
D.(,2)
3.已知反比例函数y=,当1<x≤4时,y的最大整数值是(
)
A.4
B.3
C.2
D.1
4.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表,根据表中数据,可得y关于x的函数表达式为(
)
近视眼镜的度数y(度)
200
250
400
500
1000
镜片焦距x(米)
0.50
0.40
0.25
0.20
0.10
A.y=
B.y=
C.y=
D.y=
5.反比例函数y=的图象上有两点(-2,y1),(1,y2),那么y1与y2的关系为(
)
A.y1>y2
B.y1=y2
C.y1<y2
D.不能确定
6.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴,y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=(x>0)的图象上,若AB=1,则k的值为(
)
A.1
B.
C.
D.2
7.在同一平面直角坐标系中,函数y=-x+k与y=(k为常数,且k≠0)的图象大致是(
)
8.如图,在平面直角坐标系中,Rt△ABC的顶点A,C坐标分别是(0,3),(3,0).∠ACB=90°,AC=2BC,则函数y=(k>0,x>0)的图象经过点B,则k的值为(
)
A.
B.9
C.
D.
二、填空题(本大题有8小题,每小题3分,共24分)
9.下列函数是反比例函数的有________.(只填序号)
①y=-,②y=5x-1,③y=(k为常数且k≠0),④y=.
10.双曲线y=在每个象限内,函数值y随x的增大而增大,则m的取值范围是________.
11.如图所示,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C,D在x轴上,且BC∥AD,四边形ABCD的面积为3,则这个反比例函数的表达式为________.
eq
\o(\s\up7(),\s\do5((第11题图)))
eq
\o(\s\up7(),\s\do5((第14题图)))
eq
\o(\s\up7(),\s\do5((第15题图)))
eq
\o(\s\up7(),\s\do5((第16题图)))
12.已知一个函数的图象与y=的图象关于y轴对称,则该函数的解析式为________.
13.根据某商场对一款运动鞋五天中的售价与销量关系的调查显示,售价是销量的反比例函数(统计数据见下表).已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为________元.
售价x(元/双)
200
240
250
400
销售量y(双)
30
25
24
15
14.如图,在平面直角坐标系中,点A的坐标为(-4,2),反比例函数y=(x<0)的图象经过线段OA的中点B,则k=________.
15.如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=(x>0)的图象上,顶点B在函数y2=(x>0)的图象上,∠ABO=30°,则=________.
16.如图,双曲线y=(x>0)经过矩形OABC的顶点B,双曲线y=(x>0)交AB,BC于点E,F,且与矩形的对角线OB交于点D,连接EF.若OD∶OB=2∶3,则△BEF的面积为________.
三、解答题(本大题有9小题,共72分)
17.(6分)已知反比例函数y=(k≠0)的图象经过点A(-3,-6).
(1)求这个函数的表达式;
(2)点B(4,),C(2,-5)是否在这个函数的图象上?
18.(6分)已知反比例函数y=mx|m-2|-4的图象位于第二、四象限.
(1)求m的值;
(2)若点A(x1,y1),B(x2,y2)是反比例函数图象上两点,且x1<0<x2,试比较y1,y2的大小.
19.(6分)某地建设一项水利工程,工程需要运送的土石方总量为360万立方米.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万立方米)之间的函数关系式;
(2)为了能在150天内完成任务,平均每天的工作量至少是多少万立方米?
20.(6分)如图,一次函数y1=x+1的图象与反比例函数y2=(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1.
(1)在第一象限内,当x取何值时,y1>y2?
(2)求反比例函数的表达式.
21.(7分)如图,直线y=x+b与双曲线y=(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
22.(9分)如图,在平面直角坐标系xOy中,函数y=(x>0)的图象与直线y=x-2交于点A(3,m).
(1)求k,m的值;
(2)已知点P(n,n)(n>0),过点P作平行于x轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数y=(x>0)的图象于点N.当n=1时,判断线段PM与PN的数量关系,并说明理由.
23.(10分)如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与y轴交于点C,与反比例函数y=(k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
(1)求反比例函数和一次函数的解析式;
(2)连接OB,MC,求四边形MBOC的面积.
24.(10分)如图,在平面直角坐标系xOy中,点A(3,2)在反比例函数y=(x>0)的图象上,点B在OA的延长线上,BC⊥x轴,垂足为C,BC与反比例函数的图象相交于点D,连接AC,AD.
(1)求该反比例函数的解析式;
(2)若S△ACD=,设点C的坐标为(a,0),求线段BD的长.
25.(12分)为预防疾病,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.根据以上信息,解答下列问题:
(1)求药物燃烧时y与x的函数关系式;
(2)求药物燃烧后y与x的函数关系式;
(3)当每立方米空气中含药量低于1.6mg时,对人体无毒害作用.那么从消毒开始,经过多长时间学生才可以返回教室?
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
