北京版八年级下册数学17.1 方差 课件(91张ppt)
文档属性
| 名称 | 北京版八年级下册数学17.1 方差 课件(91张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-22 10:30:55 | ||
图片预览










文档简介
(共91张PPT)
初二年级
数学
方
差
数据的分析
平均数
中位数
众
数
极
差
方
差
集中趋势
离散程度
复习引入
平均数:
1.算术平均数
把一组数据的和除以这组数据的总个数,得到的数值叫做这组数据的算术平均数,简称平均数.
平均数:
一组数据的平均数的计算公式如下:
设n个数据分别为
,
,
它们的平均数为
,则
平均数:
2.加权平均数
加权平均数的计算公式为:
若数据
出现
次,
出现
次,
出现
次
??????
出现
次,这组数据的平均数为
,
平均数:
加权平均数的计算公式为:
(其中
)
2.加权平均数
数据重复出现的次数
f
叫做这个数据的权数,简称为这个数据的权.
请你计算出下列数据的平均数.
3,3,2,4,2.
练一练:
方法一:
方法二:
一组数据中出现次数最多的那个数据,叫做这组数据的众数.
众数:
中位数:
将一组数据按大小依次排列,处于中间位置的那个数(或中间两数的平均数),叫做这组数据的中位数.
中位数:
求一组数据中位数的方法:
(1)将一组数据按大小依次排列;
(2)若一组数据的个数为奇数,则中位数为处于中间位置的那个数;若一组数据的个数为偶数,则中位数是中间两数的平均数.
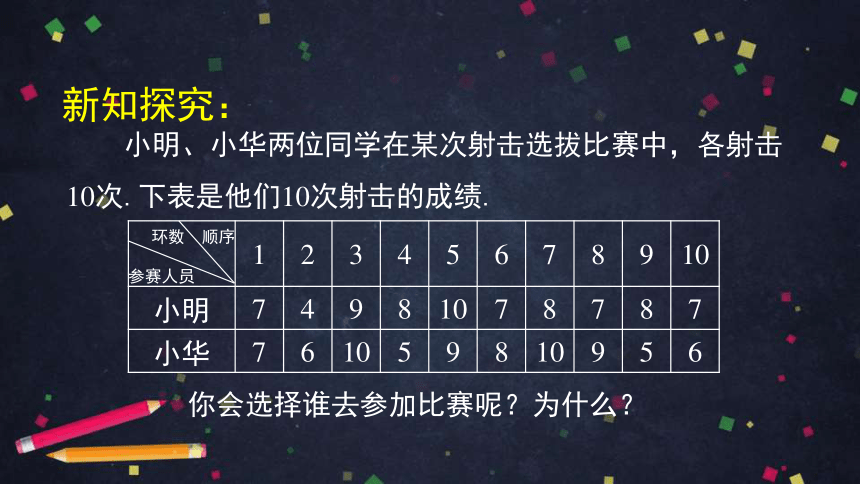
新知探究:
小明、小华两位同学在某次射击选拔比赛中,各射击10次.下表是他们10次射击的成绩.
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
你会选择谁去参加比赛呢?为什么?
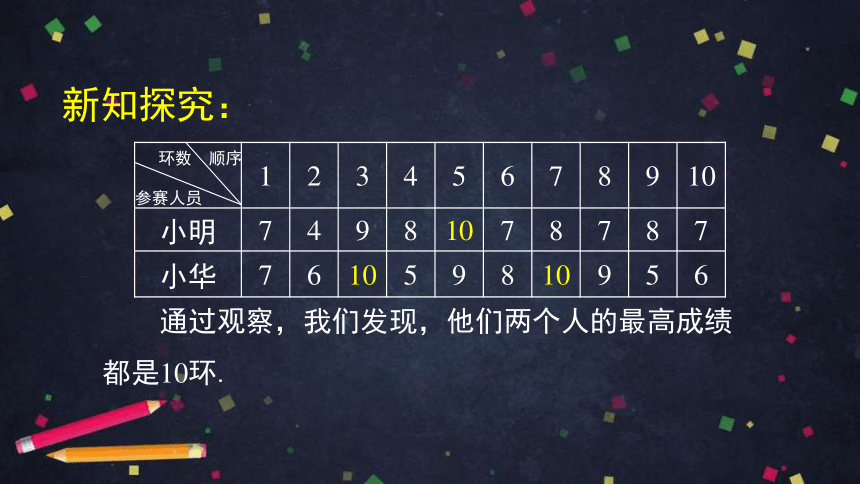
新知探究:
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
通过观察,我们发现,他们两个人的最高成绩都是10环.
新知探究:
小明、小华两位同学在某次射击选拔比赛中,各射击10次.下表是他们10次射击的成绩.
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
你会选择谁去参加比赛呢?为什么?
新知探究:
小明:4,7,
7,7,7,8,8,8,9,
10
;
小华:5,5,
6,6,7,8,9,9,10,10
.
小明成绩的中位数:
(环),
小华成绩的中位数:
(环).
新知探究:
小明、小华两位同学在某次射击选拔比赛中,各射击10次.下表是他们10次射击的成绩.
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
你会选择谁去参加比赛呢?为什么?
新知探究:
小明成绩的平均数:
小华成绩的平均数:
(环)
(环)
新知探究:
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
从两个人10次射击成绩变化范围的大小考虑.
新知探究:
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
从两个人10次射击成绩变化范围的大小考虑.
新知探究:
小明的成绩变化范围是:
最高成绩-最低成绩=10-4=6(环)
小华的成绩变化范围是:
最高成绩-最低成绩=10-5=5(环)
新知探究:
∵
6>5
∴
小华的成绩变化范围比较小,如果只从成绩的变化范围看,选派小华参加比赛较合适.
通常,我们称一组数据中的最大值减去最小值所得的差为极差.
极差的定义:
极差=数据中的最大值-数据中的最小值.
新知探究:
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
小明成绩的极差是:10-4=6
小华成绩的极差是:10-5=5
极差表示了一组数据变化范围的大小,它粗略地反映了一组数据的离散程度.
极差的统计含义:
新知探究:
为了更合理地确定派谁参加比赛,我们还要全面深入地分析他们的成绩.
分析每组数据波动的大小.
新知探究:
7.5
7.5
平均数
次
数
1
2
3
4
5
6
7
8
9
10
求
和
小
明
7.5
每次成绩
7
4
9
8
10
7
8
7
8
7
75
与平均数的差
小
华
7.5
每次成绩
7
6
10
5
9
8
10
9
5
6
75
与平均数的差
平均数
次
数
1
2
3
4
5
6
7
8
9
10
求
和
小
明
7.5
每次成绩
7
4
9
8
10
7
8
7
8
7
75
与平均数的差
-0.5
-3.5
1.5
0.5
2.5
-0.5
0.5
-0.5
0.5
-0.5
0
小
华
7.5
每次成绩
7
6
10
5
9
8
10
9
5
6
75
与平均数的差
-0.5
-1.5
2.5
-2.5
1.5
0.5
2.5
1.5
-2.5
-1.5
0
新知探究:
下面我们分别计算两个人的成绩偏离平均数的平均距离,来比较成绩波动的大小.
求每个数据与平均数的差的绝对值,再求平均值.
新知探究:
小明:
小华:
由于1.1<1.7,说明小明的成绩偏离平均数的平均距离较小,波动较小,成绩更稳定.
新知探究:
偏离平均数的平均距离比极差更全面的反映了一组数据波动的大小,但是在计算时要取绝对值,使用不便.因此,我们通常先取每个数据与平均数的差的平方数,再求平均值.
新知探究:
小明:
小华:
由于2.25<3.45,说明小明的成绩偏离平均数的平均距离波动较小,成绩更稳定.
新知探究:
虽然小华的10次成绩变化范围较小,但是从成绩波动情况看,小明的成绩波动较小,更稳定,如果选派“稳定型”选手参加比赛,选派小明参加比赛更加合适.
新知探究:
如果用
,
,
,
,
表示一组数据,用
表示这组数据的平均数,用
表示每个数据与平均数的差的平方数的平均值.
你能写出
的计算公式吗?
…
的计算公式是:
我们把
叫做这组数据
,
,
,
,
的方差.
方差的定义:
…
(1)方差描述了一组数据波动的大小.
(2)方差越小,数据波动越小,越整齐.
方差的统计含义:
例1:
某地区某年12月中旬前、后5天的最高气温记录如下(单位:℃):
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
比较哪5天中最高气温的变化范围较小,哪5天中最高气温的波动较小.
分析:要比较最高气温变化范围的大小,只需要计算并比较它们的极差.
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
例1:
分析:要比较最高气温变化范围的大小,只需要计算并比较它们的极差.
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
例1:
分析:要比较最高气温变化范围的大小,只需要计算并比较它们的极差.
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
例1:
前5天:极差1=5-0=5
分析:要比较最高气温变化范围的大小,只需要计算并比较它们的极差.
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
例1:
分析:要比较最高气温变化范围的大小,只需要计算并比较它们的极差.
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
例1:
后5天:极差2=5-(-1)=6
因为极差1<极差2,所以前5天中最高气温的变化范围小.
后5天:极差2=5-(-1)=6.
前5天:极差1=5-0=5;
例1:
分析:要比较最高气温波动的大小,只需要计算并比较它们的方差.
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
例1:
计算方差的步骤如下:
(1)先求这两组数据的平均数.
例1:
(2)再把数据代入方差计算公式计算.
前5天:
后5天:
例1:
因为
,所以后5天中最高气温的波动较小,比较稳定.
小结:
1.
极差的定义及计算方法:
通常,我们称一组数据中的最大值减去最小值所得的差为极差.
极差=数据中的最大值-数据中的最小值.
小结:
2.
计算一组数据方差的步骤:
(1)先求这组数据的平均数;
(2)再把数据代入方差计算公式计算.
小结:
3.极差和方差的统计含义
极差描述了一组数据变化范围的大小;方差描述了一组数据波动的大小.
极差粗略地反映了一组数据的离散程度,方差全面地平均地反映了一组数据的离散程度.
小结:
4.
方差越小,数据波动越小,越整齐;
方差越大,数据波动越大,越离散.
例2:
种子研究基地计划为某地选择合适的水稻种子.选择种子时,水稻的产量和产量的稳定性是种子研究基地所关心的问题.为了解甲、乙两种水稻种子的相关情况,各用10块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)
例2:
如下表所示:
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
根据这些数据估计,种子研究基地应该选择哪种水稻种子呢?
例2:
分析:
通过审题可知,水稻的产量和产量的稳定性是种子研究基地所关心的问题.
解决本题的关键是,计算出样本的平均数和方差,利用样本估计总体的方法,解决问题.
例2:
上面两组数据的平均数分别是:
说明在试验田中,甲、乙两种水稻的平均产量相差不大,由此可以估计出这个地区种植这两种水稻,它们的平均产量相差不大.
用样本估计总体.
例2:
下面我们利用方差来分析甲,乙两种水稻产量波动的大小.
例2:
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
例2:
上面两组数据的方差分别是:
由于
,所以乙种水稻产量的波动较小.
例2:
综合考虑甲,乙两个品种的平均产量和产量的稳定性,可以推测这个地区比较适合种植乙种水稻.
小结:
1.当两组数据的平均数相等或近似相等时,可以用方差来比较两组数据的离散程度.
小结:
2.方差的应用主要有以下两方面:
(1)直接用方差的大小比较两个总体特征的
差异;
(2)用两个样本的方差的大小估计相应两个
总体特征的差异.
例3:
某校要从李勇、张浩两名学生中挑选一人参加区级跳远比赛,在跳远专项测试及之后的6次跳远选拔赛中,他们的成绩(单位:cm)如下表所示:
例3:
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
张浩
597
580
597
630
590
631
596
333
李勇、张浩专项测试和6次跳远选拔赛成绩如下表:
例3:
(1)求张浩同学7次测试成绩的平均数,李勇同学7次测试成绩的方差;(所得的结果取整)
(2)请你分别从平均数和方差的角度分析两人成绩的特点;
例3:
(3)历届比赛成绩表明,成绩若达到600cm就很有可能得冠军,你认为应选谁去参加比赛夺冠比较有把握?说明理由;
例3:
(4)以往该项成绩的纪录是615cm,若想打
破纪录,你认为应选谁去参赛?
例3:
(1)求张浩同学7次测试成绩的平均数,李勇同学7次测试成绩的方差;(所得的结果取整)
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
张浩
597
580
597
630
590
631
596
333
例3:
分析:要求平均数和方差,只要代入相应的公式计算即可.
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
张浩
597
580
597
630
590
631
596
333
例3:
分析:要求平均数和方差,只要代入相应的公式计算即可.
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
例3:
(2)请你分别从平均数和方差的角度分析两人成绩的特点;
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
例3:
分析:平均数描述一组数据的集中趋势;方差描述一组数据的离散程度.
例3:
平均数/cm
方差/cm2
李勇
602
49
张浩
603
333
解:从成绩的平均数来
看,张浩成绩的平均水平比
李勇的高;从成绩的方差来看,李勇的成绩比张浩的稳定.
例3:
(3)历届比赛成绩表明,成绩若达到600cm就很有可能得冠军,你认为应选谁去参加比赛夺冠比较有把握?说明理由;
例3:
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
分析:选谁参加比赛夺冠比较有把握,只需要比较两名同学超过600cm的次数.
例3:
分析:选谁参加比赛夺冠比较有把握,只需要比较两名同学超过600cm的次数.
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
例3:
解:在专项测试和6次跳远选拔赛中,李勇有5次成绩超过600cm,而张浩只有两次成绩超过600cm,所以选李勇参加比赛夺冠有把握.
例3:
(4)以往该项成绩的纪录是615cm,若想打破纪录,你认为应选谁去参赛?
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
例3:
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
分析:若想打破纪录,需要比较他们成绩超过615
cm的次数.
例3:
解:张浩有两次成绩超过615cm,而李勇没有一次达到615cm,所以选张浩去参赛.
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
小结:
不同的统计量使用的范围不同,要根据实际问题的需要,选择合适的统计量来刻画数据.
课堂小结:
1.极差和方差的定义及计算公式
(1)极差的定义及计算公式
通常,我们称一组数据中的最大值减去最小值所得的差为极差.极差=数据中的最大值-数据中的最小值.
课堂小结:
1.极差和方差的定义及计算公式
(2)方差的定义及计算公式
我们把
叫做这组数据
,
,
,
,
的方差.
…
课堂小结:
(1)先求这组数据的平均数;
(2)再把数据代入方差计算公式计算.
2.方差的计算步骤
课堂小结:
(1)极差和方差都反映了一组数据的波动大小,
离散程度,我们常用方差来比较平均数相等或近
似相等的两组数据的离散程度.
3.极差和方差的统计含义
课堂小结:
(2)方差越小,数据的波动越小;
方差越大,数据的波动越大.
3.极差和方差的统计含义
课堂小结:
数据的集中趋势
数据的离散程度
平均数
中位数
众
数
极
差
方
差
用
样
本
估
计
总
体
用样本平均数估计总体平均数
用样本方差估计总体方差
课后作业:
A组:
比较下列两组数据,哪组数据的变化范围较小,哪组数据的波动较小、比较整齐.
甲
组
1
3
5
7
9
乙
组
-1
2
9
10
-
课后作业:
B组:
小华在一次运动员集训前、后的各5次百米跑中,测验成绩如下表(单位:s).
集训前
11.3
11.2
11.4
11.5
11.7
集训后
11.6
11.3
11.4
11.2
11.3
课后作业:
B组:
请你用数据说明,这次集训对小华的百米跑成绩的提高是否有效果,如果有效果,效果表现在哪些方面.
练一练
在一次外语测验中,同年级人数相同的甲、乙两个班的成绩统计如下表:
班级
平均分
中位数
方差
甲班
82.5
85.5
40.25
乙班
82.5
80.5
35.06
练一练
一位同学对此做出如下评估:
?
这次外语测验成绩甲、乙两个班的平均水平相同;
?
甲班学生中成绩优秀(85分及以上)的多;
?
乙班学生的成绩比较整齐,分化较小.
上述评估,正确的是
(填序号).
练一练
在一次外语测验中,同年级人数相同的甲、乙两个班的成绩统计如下表:
班级
平均分
中位数
方差
甲班
82.5
85.5
40.25
乙班
82.5
80.5
35.06
练一练
一位同学对此做出了如下评估:
?
这次外语测验成绩甲、乙两个班的平均水平相同;
?
甲班学生中成绩优秀(85分及以上)的多;
?
乙班学生的成绩比较整齐,分化较小.
上述评估,正确的是
???
(填序号).
初二年级
数学
方
差
数据的分析
平均数
中位数
众
数
极
差
方
差
集中趋势
离散程度
复习引入
平均数:
1.算术平均数
把一组数据的和除以这组数据的总个数,得到的数值叫做这组数据的算术平均数,简称平均数.
平均数:
一组数据的平均数的计算公式如下:
设n个数据分别为
,
,
它们的平均数为
,则
平均数:
2.加权平均数
加权平均数的计算公式为:
若数据
出现
次,
出现
次,
出现
次
??????
出现
次,这组数据的平均数为
,
平均数:
加权平均数的计算公式为:
(其中
)
2.加权平均数
数据重复出现的次数
f
叫做这个数据的权数,简称为这个数据的权.
请你计算出下列数据的平均数.
3,3,2,4,2.
练一练:
方法一:
方法二:
一组数据中出现次数最多的那个数据,叫做这组数据的众数.
众数:
中位数:
将一组数据按大小依次排列,处于中间位置的那个数(或中间两数的平均数),叫做这组数据的中位数.
中位数:
求一组数据中位数的方法:
(1)将一组数据按大小依次排列;
(2)若一组数据的个数为奇数,则中位数为处于中间位置的那个数;若一组数据的个数为偶数,则中位数是中间两数的平均数.
新知探究:
小明、小华两位同学在某次射击选拔比赛中,各射击10次.下表是他们10次射击的成绩.
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
你会选择谁去参加比赛呢?为什么?
新知探究:
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
通过观察,我们发现,他们两个人的最高成绩都是10环.
新知探究:
小明、小华两位同学在某次射击选拔比赛中,各射击10次.下表是他们10次射击的成绩.
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
你会选择谁去参加比赛呢?为什么?
新知探究:
小明:4,7,
7,7,7,8,8,8,9,
10
;
小华:5,5,
6,6,7,8,9,9,10,10
.
小明成绩的中位数:
(环),
小华成绩的中位数:
(环).
新知探究:
小明、小华两位同学在某次射击选拔比赛中,各射击10次.下表是他们10次射击的成绩.
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
你会选择谁去参加比赛呢?为什么?
新知探究:
小明成绩的平均数:
小华成绩的平均数:
(环)
(环)
新知探究:
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
从两个人10次射击成绩变化范围的大小考虑.
新知探究:
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
从两个人10次射击成绩变化范围的大小考虑.
新知探究:
小明的成绩变化范围是:
最高成绩-最低成绩=10-4=6(环)
小华的成绩变化范围是:
最高成绩-最低成绩=10-5=5(环)
新知探究:
∵
6>5
∴
小华的成绩变化范围比较小,如果只从成绩的变化范围看,选派小华参加比赛较合适.
通常,我们称一组数据中的最大值减去最小值所得的差为极差.
极差的定义:
极差=数据中的最大值-数据中的最小值.
新知探究:
1
2
3
4
5
6
7
8
9
10
小明
7
4
9
8
10
7
8
7
8
7
小华
7
6
10
5
9
8
10
9
5
6
顺序
环数
参赛人员
小明成绩的极差是:10-4=6
小华成绩的极差是:10-5=5
极差表示了一组数据变化范围的大小,它粗略地反映了一组数据的离散程度.
极差的统计含义:
新知探究:
为了更合理地确定派谁参加比赛,我们还要全面深入地分析他们的成绩.
分析每组数据波动的大小.
新知探究:
7.5
7.5
平均数
次
数
1
2
3
4
5
6
7
8
9
10
求
和
小
明
7.5
每次成绩
7
4
9
8
10
7
8
7
8
7
75
与平均数的差
小
华
7.5
每次成绩
7
6
10
5
9
8
10
9
5
6
75
与平均数的差
平均数
次
数
1
2
3
4
5
6
7
8
9
10
求
和
小
明
7.5
每次成绩
7
4
9
8
10
7
8
7
8
7
75
与平均数的差
-0.5
-3.5
1.5
0.5
2.5
-0.5
0.5
-0.5
0.5
-0.5
0
小
华
7.5
每次成绩
7
6
10
5
9
8
10
9
5
6
75
与平均数的差
-0.5
-1.5
2.5
-2.5
1.5
0.5
2.5
1.5
-2.5
-1.5
0
新知探究:
下面我们分别计算两个人的成绩偏离平均数的平均距离,来比较成绩波动的大小.
求每个数据与平均数的差的绝对值,再求平均值.
新知探究:
小明:
小华:
由于1.1<1.7,说明小明的成绩偏离平均数的平均距离较小,波动较小,成绩更稳定.
新知探究:
偏离平均数的平均距离比极差更全面的反映了一组数据波动的大小,但是在计算时要取绝对值,使用不便.因此,我们通常先取每个数据与平均数的差的平方数,再求平均值.
新知探究:
小明:
小华:
由于2.25<3.45,说明小明的成绩偏离平均数的平均距离波动较小,成绩更稳定.
新知探究:
虽然小华的10次成绩变化范围较小,但是从成绩波动情况看,小明的成绩波动较小,更稳定,如果选派“稳定型”选手参加比赛,选派小明参加比赛更加合适.
新知探究:
如果用
,
,
,
,
表示一组数据,用
表示这组数据的平均数,用
表示每个数据与平均数的差的平方数的平均值.
你能写出
的计算公式吗?
…
的计算公式是:
我们把
叫做这组数据
,
,
,
,
的方差.
方差的定义:
…
(1)方差描述了一组数据波动的大小.
(2)方差越小,数据波动越小,越整齐.
方差的统计含义:
例1:
某地区某年12月中旬前、后5天的最高气温记录如下(单位:℃):
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
比较哪5天中最高气温的变化范围较小,哪5天中最高气温的波动较小.
分析:要比较最高气温变化范围的大小,只需要计算并比较它们的极差.
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
例1:
分析:要比较最高气温变化范围的大小,只需要计算并比较它们的极差.
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
例1:
分析:要比较最高气温变化范围的大小,只需要计算并比较它们的极差.
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
例1:
前5天:极差1=5-0=5
分析:要比较最高气温变化范围的大小,只需要计算并比较它们的极差.
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
例1:
分析:要比较最高气温变化范围的大小,只需要计算并比较它们的极差.
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
例1:
后5天:极差2=5-(-1)=6
因为极差1<极差2,所以前5天中最高气温的变化范围小.
后5天:极差2=5-(-1)=6.
前5天:极差1=5-0=5;
例1:
分析:要比较最高气温波动的大小,只需要计算并比较它们的方差.
前5天
5
5
0
0
0
后5天
-1
2
2
2
5
例1:
计算方差的步骤如下:
(1)先求这两组数据的平均数.
例1:
(2)再把数据代入方差计算公式计算.
前5天:
后5天:
例1:
因为
,所以后5天中最高气温的波动较小,比较稳定.
小结:
1.
极差的定义及计算方法:
通常,我们称一组数据中的最大值减去最小值所得的差为极差.
极差=数据中的最大值-数据中的最小值.
小结:
2.
计算一组数据方差的步骤:
(1)先求这组数据的平均数;
(2)再把数据代入方差计算公式计算.
小结:
3.极差和方差的统计含义
极差描述了一组数据变化范围的大小;方差描述了一组数据波动的大小.
极差粗略地反映了一组数据的离散程度,方差全面地平均地反映了一组数据的离散程度.
小结:
4.
方差越小,数据波动越小,越整齐;
方差越大,数据波动越大,越离散.
例2:
种子研究基地计划为某地选择合适的水稻种子.选择种子时,水稻的产量和产量的稳定性是种子研究基地所关心的问题.为了解甲、乙两种水稻种子的相关情况,各用10块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)
例2:
如下表所示:
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
根据这些数据估计,种子研究基地应该选择哪种水稻种子呢?
例2:
分析:
通过审题可知,水稻的产量和产量的稳定性是种子研究基地所关心的问题.
解决本题的关键是,计算出样本的平均数和方差,利用样本估计总体的方法,解决问题.
例2:
上面两组数据的平均数分别是:
说明在试验田中,甲、乙两种水稻的平均产量相差不大,由此可以估计出这个地区种植这两种水稻,它们的平均产量相差不大.
用样本估计总体.
例2:
下面我们利用方差来分析甲,乙两种水稻产量波动的大小.
例2:
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
例2:
上面两组数据的方差分别是:
由于
,所以乙种水稻产量的波动较小.
例2:
综合考虑甲,乙两个品种的平均产量和产量的稳定性,可以推测这个地区比较适合种植乙种水稻.
小结:
1.当两组数据的平均数相等或近似相等时,可以用方差来比较两组数据的离散程度.
小结:
2.方差的应用主要有以下两方面:
(1)直接用方差的大小比较两个总体特征的
差异;
(2)用两个样本的方差的大小估计相应两个
总体特征的差异.
例3:
某校要从李勇、张浩两名学生中挑选一人参加区级跳远比赛,在跳远专项测试及之后的6次跳远选拔赛中,他们的成绩(单位:cm)如下表所示:
例3:
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
张浩
597
580
597
630
590
631
596
333
李勇、张浩专项测试和6次跳远选拔赛成绩如下表:
例3:
(1)求张浩同学7次测试成绩的平均数,李勇同学7次测试成绩的方差;(所得的结果取整)
(2)请你分别从平均数和方差的角度分析两人成绩的特点;
例3:
(3)历届比赛成绩表明,成绩若达到600cm就很有可能得冠军,你认为应选谁去参加比赛夺冠比较有把握?说明理由;
例3:
(4)以往该项成绩的纪录是615cm,若想打
破纪录,你认为应选谁去参赛?
例3:
(1)求张浩同学7次测试成绩的平均数,李勇同学7次测试成绩的方差;(所得的结果取整)
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
张浩
597
580
597
630
590
631
596
333
例3:
分析:要求平均数和方差,只要代入相应的公式计算即可.
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
张浩
597
580
597
630
590
631
596
333
例3:
分析:要求平均数和方差,只要代入相应的公式计算即可.
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
例3:
(2)请你分别从平均数和方差的角度分析两人成绩的特点;
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
例3:
分析:平均数描述一组数据的集中趋势;方差描述一组数据的离散程度.
例3:
平均数/cm
方差/cm2
李勇
602
49
张浩
603
333
解:从成绩的平均数来
看,张浩成绩的平均水平比
李勇的高;从成绩的方差来看,李勇的成绩比张浩的稳定.
例3:
(3)历届比赛成绩表明,成绩若达到600cm就很有可能得冠军,你认为应选谁去参加比赛夺冠比较有把握?说明理由;
例3:
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
分析:选谁参加比赛夺冠比较有把握,只需要比较两名同学超过600cm的次数.
例3:
分析:选谁参加比赛夺冠比较有把握,只需要比较两名同学超过600cm的次数.
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
例3:
解:在专项测试和6次跳远选拔赛中,李勇有5次成绩超过600cm,而张浩只有两次成绩超过600cm,所以选李勇参加比赛夺冠有把握.
例3:
(4)以往该项成绩的纪录是615cm,若想打破纪录,你认为应选谁去参赛?
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
例3:
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
分析:若想打破纪录,需要比较他们成绩超过615
cm的次数.
例3:
解:张浩有两次成绩超过615cm,而李勇没有一次达到615cm,所以选张浩去参赛.
专项测试和6次跳远选拔赛成绩
/cm
平均数/cm
方差/cm2
李勇
603
589
602
596
604
612
608
602
49
张浩
597
580
597
630
590
631
596
603
333
小结:
不同的统计量使用的范围不同,要根据实际问题的需要,选择合适的统计量来刻画数据.
课堂小结:
1.极差和方差的定义及计算公式
(1)极差的定义及计算公式
通常,我们称一组数据中的最大值减去最小值所得的差为极差.极差=数据中的最大值-数据中的最小值.
课堂小结:
1.极差和方差的定义及计算公式
(2)方差的定义及计算公式
我们把
叫做这组数据
,
,
,
,
的方差.
…
课堂小结:
(1)先求这组数据的平均数;
(2)再把数据代入方差计算公式计算.
2.方差的计算步骤
课堂小结:
(1)极差和方差都反映了一组数据的波动大小,
离散程度,我们常用方差来比较平均数相等或近
似相等的两组数据的离散程度.
3.极差和方差的统计含义
课堂小结:
(2)方差越小,数据的波动越小;
方差越大,数据的波动越大.
3.极差和方差的统计含义
课堂小结:
数据的集中趋势
数据的离散程度
平均数
中位数
众
数
极
差
方
差
用
样
本
估
计
总
体
用样本平均数估计总体平均数
用样本方差估计总体方差
课后作业:
A组:
比较下列两组数据,哪组数据的变化范围较小,哪组数据的波动较小、比较整齐.
甲
组
1
3
5
7
9
乙
组
-1
2
9
10
-
课后作业:
B组:
小华在一次运动员集训前、后的各5次百米跑中,测验成绩如下表(单位:s).
集训前
11.3
11.2
11.4
11.5
11.7
集训后
11.6
11.3
11.4
11.2
11.3
课后作业:
B组:
请你用数据说明,这次集训对小华的百米跑成绩的提高是否有效果,如果有效果,效果表现在哪些方面.
练一练
在一次外语测验中,同年级人数相同的甲、乙两个班的成绩统计如下表:
班级
平均分
中位数
方差
甲班
82.5
85.5
40.25
乙班
82.5
80.5
35.06
练一练
一位同学对此做出如下评估:
?
这次外语测验成绩甲、乙两个班的平均水平相同;
?
甲班学生中成绩优秀(85分及以上)的多;
?
乙班学生的成绩比较整齐,分化较小.
上述评估,正确的是
(填序号).
练一练
在一次外语测验中,同年级人数相同的甲、乙两个班的成绩统计如下表:
班级
平均分
中位数
方差
甲班
82.5
85.5
40.25
乙班
82.5
80.5
35.06
练一练
一位同学对此做出了如下评估:
?
这次外语测验成绩甲、乙两个班的平均水平相同;
?
甲班学生中成绩优秀(85分及以上)的多;
?
乙班学生的成绩比较整齐,分化较小.
上述评估,正确的是
???
(填序号).
同课章节目录
