人教版八年级下册数学 18.2.1矩形 同步测试含答案
文档属性
| 名称 | 人教版八年级下册数学 18.2.1矩形 同步测试含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 270.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-21 06:49:59 | ||
图片预览

文档简介
18.2.1矩形
同步测试
一、选择题
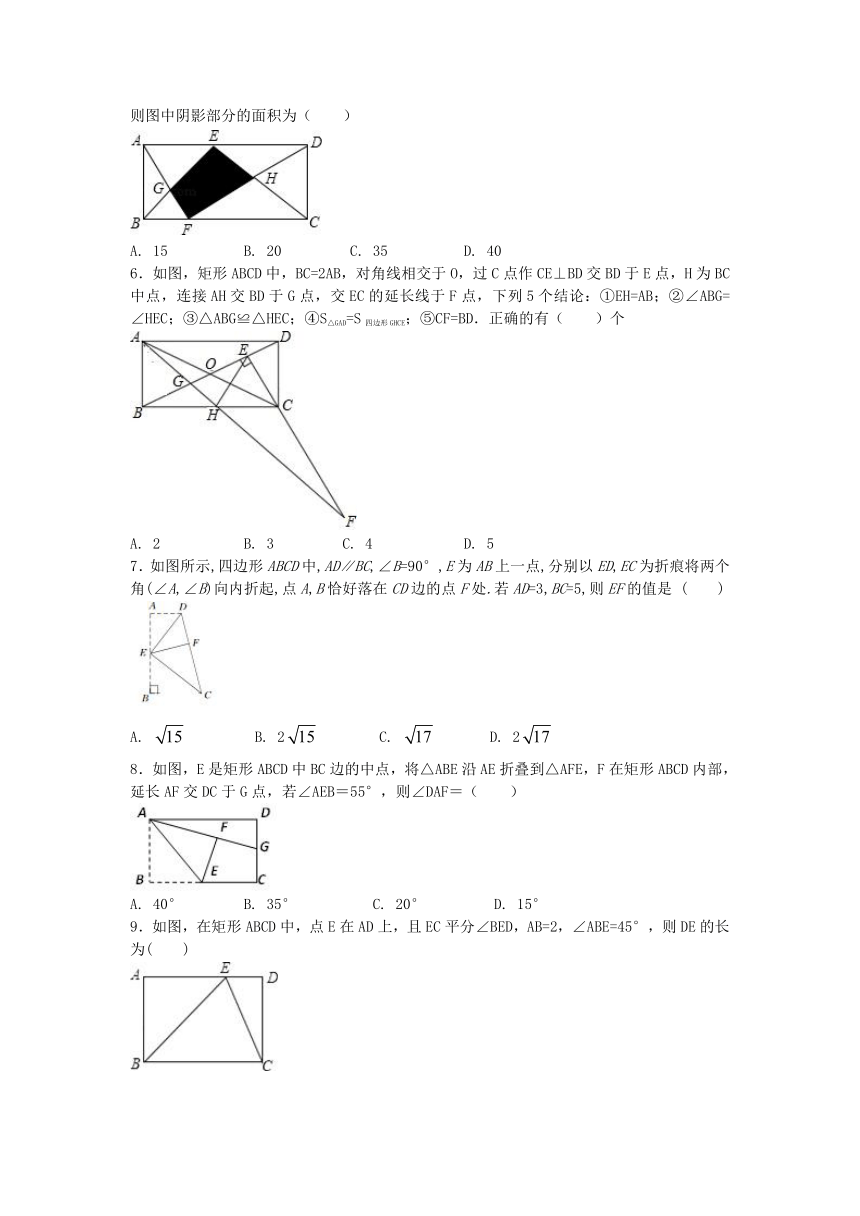
1.下列叙述错误的是(
)
A.
平行四边形的对角线互相平分
B.
对角线互相平分的四边形是平行四边形
C.
矩形的对角线相等
D.
对角线相等的四边形是矩形
2.如图,四边形ABCD的对角线AC、BD相交于点O,且AC=BD,则下列条件能判定四边形ABCD为矩形的是(
)
A.
AB=CD
B.
OA=OC,OB=OD
C.
AC⊥BD
D.
AB∥CD,AD=BC
3.如已知:线段AB,BC,∠ABC
=
90°.
求作:矩形ABCD.
以下是甲、乙两同学的作业:
对于两人的作业,下列说法正确的是(
)
A.
两人都对
B.
两人都不对
C.
甲对,乙不对
D.
甲不对,乙对
4.矩形ABCD中,E,F,M为AB,BC,CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM的长为( )
A.
5
B.
C.
6
D.
5.如图,E,F分别是矩形ABCD边AD、BC上的点,且△ABG,△DCH的面积分别为15和20,则图中阴影部分的面积为( )
A.
15
B.
20
C.
35
D.
40
6.如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE;⑤CF=BD.正确的有( )个
A.
2
B.
3
C.
4
D.
5
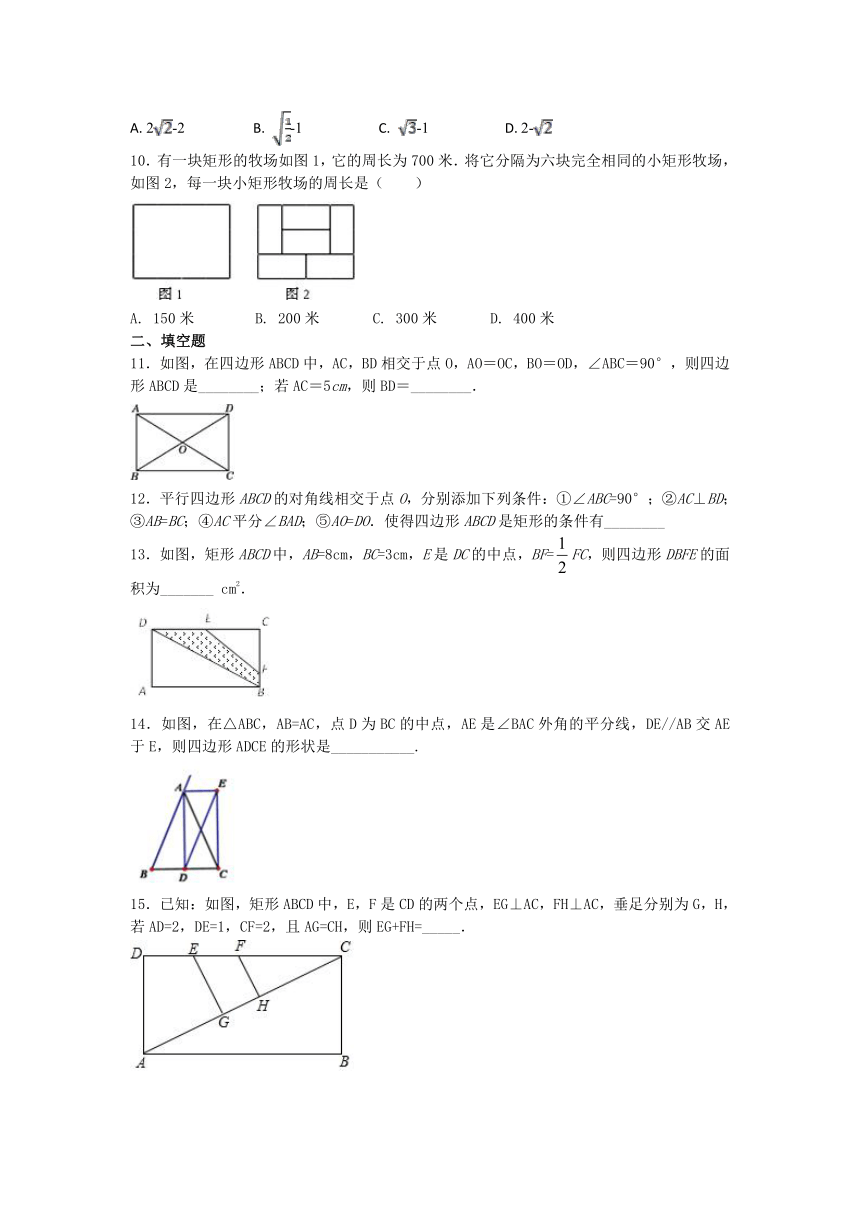
7.如图所示,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=3,BC=5,则EF的值是
( )
A.
B.
2
C.
D.
2
8.如图,E是矩形ABCD中BC边的中点,将△ABE沿AE折叠到△AFE,F在矩形ABCD内部,延长AF交DC于G点,若∠AEB=55°,则∠DAF=(
)
A.
40°
B.
35°
C.
20°
D.
15°
9.如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=2,∠ABE=45°,则DE的长为( )
A.
2-2
B.
-1
C.
-1
D.
2-
10.有一块矩形的牧场如图1,它的周长为700米.将它分隔为六块完全相同的小矩形牧场,如图2,每一块小矩形牧场的周长是(
)
A.
150米
B.
200米
C.
300米
D.
400米
二、填空题
11.如图,在四边形ABCD中,AC,BD相交于点O,AO=OC,BO=OD,∠ABC=90°,则四边形ABCD是________;若AC=5cm,则BD=________.
12.平行四边形ABCD的对角线相交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AB=BC;④AC平分∠BAD;⑤AO=DO.使得四边形ABCD是矩形的条件有________
13.如图,矩形ABCD中,AB=8cm,BC=3cm,E是DC的中点,BF=FC,则四边形DBFE的面积为_______
cm2.
14.如图,在△ABC,AB=AC,点D为BC的中点,AE是∠BAC外角的平分线,DE//AB交AE于E,则四边形ADCE的形状是___________.
15.已知:如图,矩形ABCD中,E,F是CD的两个点,EG⊥AC,FH⊥AC,垂足分别为G,H,若AD=2,DE=1,CF=2,且AG=CH,则EG+FH=_____.
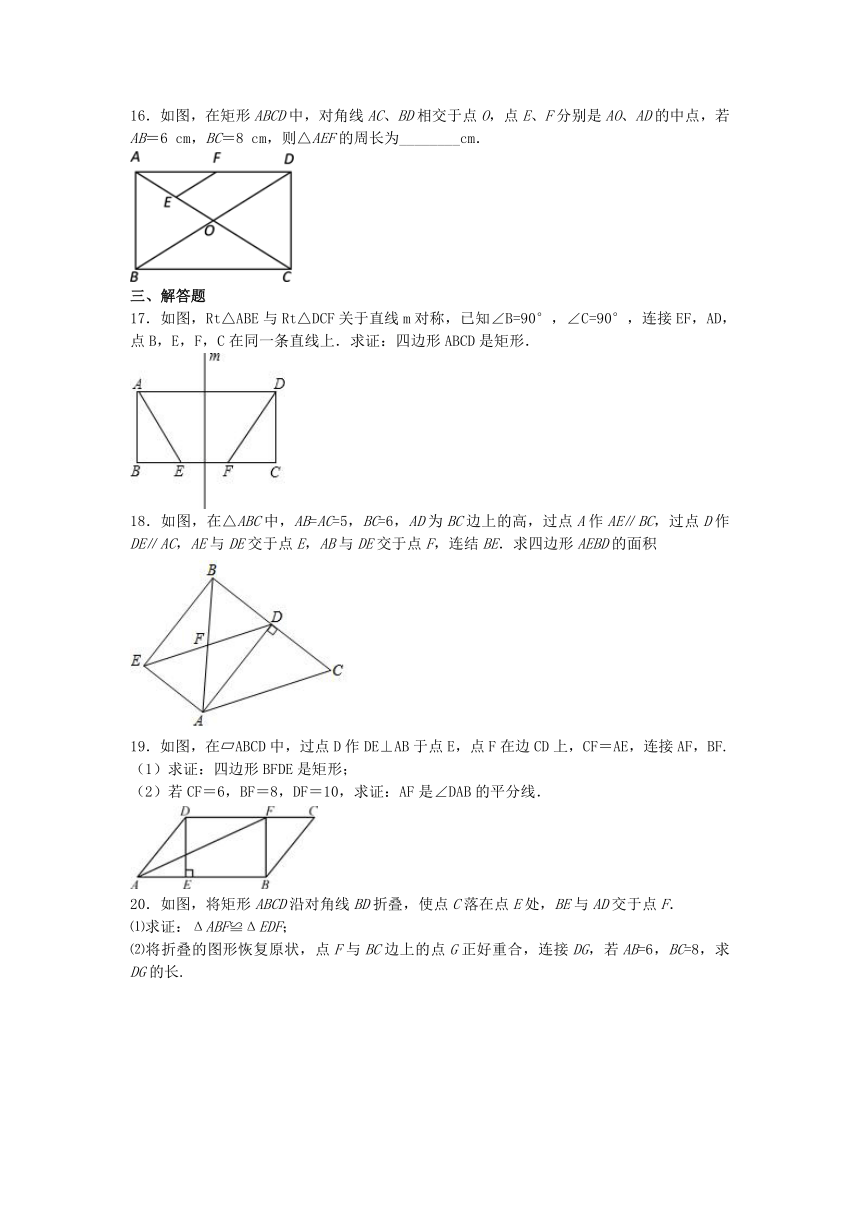
16.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6
cm,BC=8
cm,则△AEF的周长为________cm.
三、解答题
17.如图,Rt△ABE与Rt△DCF关于直线m对称,已知∠B=90°,∠C=90°,连接EF,AD,点B,E,F,C在同一条直线上.求证:四边形ABCD是矩形.
18.如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积
19.如图,在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.
20.如图,将矩形ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵将折叠的图形恢复原状,点F与BC边上的点G正好重合,连接DG,若AB=6,BC=8,求DG的长.
21.如图,在?ABCD中,各内角的平分线分别相交于点E,F,G,H.
(1)求证:△ABG≌△CDE;
(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;
(3)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.
22.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?
并说明理由.
参考答案
1.D
2.B
3.A
4.B
5.C
6.B
7.A
8.C
9.A
10.C
11.矩形
5cm
12.①⑤
13.8
14.矩形
15.
16.9
17.解析:
解:∵Rt△ABE与Rt△DCF关于直线m对称,
∴AB=DC.
∵∠B=90°,∠C=90°,点B,E,F,C在同一条直线上,
∴AB∥CD.
∴四边形ABCD是平行四边形.
∵∠B=90°,∴平行四边形ABCD是矩形.
18.12.
解析:解:∵AE∥BC,BE∥AC,∴四边形AEDC是平行四边形,∴AE=CD.
在△ABC中,AB=AC,AD为BC边上的高,∴∠ADB=90°,BD=CD,∴BD=AE,∴平行四边形AEBD是矩形.
在Rt△ADC中,∠ADB=90°,AC=5,CD=BC=3,∴AD==4,∴四边形AEBD的面积为:BD?AD=CD?AD=3×4=12.
19.
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵CF=AE,
∴BE=DF.
又∵BE∥DF,
∴四边形BFDE为平行四边形.
∵DE⊥AB,
∴∠DEB=90°.
∴四边形BFDE是矩形.
(2)∵四边形BFDE是矩形,
∴∠BFD=90°.∴∠BFC=90°.
在Rt△BFC中,由勾股定理,得BC===10.
∴AD=BC=10.
又∵DF=10,
∴AD=DF.
∴∠DAF=∠DFA.
∵AB∥CD,
∴∠DFA=∠FAB.
∴∠DAF=∠FAB.
∴AF是∠DAB的平分线.
20.(1)证明见解析;(2)
证明:在矩形ABCD中,AB=CD,
,
由折叠的性质可知:DE=CD,
,
∴AB=DE,
,
又∵,
∴△ABF≌△EDF(AAS)
(2)解:∵AD//BC,∴,由折叠的性质可知:
∴
∴BG=DG
设GC为,则BG=DG=8-x
在Rt△DCG中,由勾股定理可得:
解得:
21.(1)证明见解析;(2)矩形;(3).
解析:解:(1)∵GA平分∠BAD,EC平分∠BCD,∴∠BAG=∠BAD,∠DCE=∠DCB,∵?ABCD中,∠BAD=∠DCB,AB=CD,∴∠BAG=∠DCE,同理可得,∠ABG=∠CDE,在△ABG和△CDE中,∵∠BAG=∠DCE,AB=CD,∠ABG=∠CDE,∴△ABG≌△CDE(ASA);
(2)四边形EFGH是矩形.
证明:∵GA平分∠BAD,GB平分∠ABC,∴∠GAB=∠BAD,∠GBA=∠ABC,∵?ABCD中,∠DAB+∠ABC=180°,∴∠GAB+∠GBA=(∠DAB+∠ABC)=90°,即∠AGB=90°,同理可得,∠DEC=90°,∠AHD=90°=∠EHG,∴四边形EFGH是矩形;
(3)依题意得,∠BAG=∠BAD=30°,∵AB=6,∴BG=AB=3,AG==CE,∵BC=4,∠BCF=∠BCD=30°,∴BF=BC=2,CF=,∴EF=﹣=,GF=3﹣2=1,∴矩形EFGH的面积=EF×GF=.
22.试题解析:(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF==10,
∴OC=EF=5;
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
同步测试
一、选择题
1.下列叙述错误的是(
)
A.
平行四边形的对角线互相平分
B.
对角线互相平分的四边形是平行四边形
C.
矩形的对角线相等
D.
对角线相等的四边形是矩形
2.如图,四边形ABCD的对角线AC、BD相交于点O,且AC=BD,则下列条件能判定四边形ABCD为矩形的是(
)
A.
AB=CD
B.
OA=OC,OB=OD
C.
AC⊥BD
D.
AB∥CD,AD=BC
3.如已知:线段AB,BC,∠ABC
=
90°.
求作:矩形ABCD.
以下是甲、乙两同学的作业:
对于两人的作业,下列说法正确的是(
)
A.
两人都对
B.
两人都不对
C.
甲对,乙不对
D.
甲不对,乙对
4.矩形ABCD中,E,F,M为AB,BC,CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM的长为( )
A.
5
B.
C.
6
D.
5.如图,E,F分别是矩形ABCD边AD、BC上的点,且△ABG,△DCH的面积分别为15和20,则图中阴影部分的面积为( )
A.
15
B.
20
C.
35
D.
40
6.如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE;⑤CF=BD.正确的有( )个
A.
2
B.
3
C.
4
D.
5
7.如图所示,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=3,BC=5,则EF的值是
( )
A.
B.
2
C.
D.
2
8.如图,E是矩形ABCD中BC边的中点,将△ABE沿AE折叠到△AFE,F在矩形ABCD内部,延长AF交DC于G点,若∠AEB=55°,则∠DAF=(
)
A.
40°
B.
35°
C.
20°
D.
15°
9.如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=2,∠ABE=45°,则DE的长为( )
A.
2-2
B.
-1
C.
-1
D.
2-
10.有一块矩形的牧场如图1,它的周长为700米.将它分隔为六块完全相同的小矩形牧场,如图2,每一块小矩形牧场的周长是(
)
A.
150米
B.
200米
C.
300米
D.
400米
二、填空题
11.如图,在四边形ABCD中,AC,BD相交于点O,AO=OC,BO=OD,∠ABC=90°,则四边形ABCD是________;若AC=5cm,则BD=________.
12.平行四边形ABCD的对角线相交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AB=BC;④AC平分∠BAD;⑤AO=DO.使得四边形ABCD是矩形的条件有________
13.如图,矩形ABCD中,AB=8cm,BC=3cm,E是DC的中点,BF=FC,则四边形DBFE的面积为_______
cm2.
14.如图,在△ABC,AB=AC,点D为BC的中点,AE是∠BAC外角的平分线,DE//AB交AE于E,则四边形ADCE的形状是___________.
15.已知:如图,矩形ABCD中,E,F是CD的两个点,EG⊥AC,FH⊥AC,垂足分别为G,H,若AD=2,DE=1,CF=2,且AG=CH,则EG+FH=_____.
16.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6
cm,BC=8
cm,则△AEF的周长为________cm.
三、解答题
17.如图,Rt△ABE与Rt△DCF关于直线m对称,已知∠B=90°,∠C=90°,连接EF,AD,点B,E,F,C在同一条直线上.求证:四边形ABCD是矩形.
18.如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积
19.如图,在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.
20.如图,将矩形ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵将折叠的图形恢复原状,点F与BC边上的点G正好重合,连接DG,若AB=6,BC=8,求DG的长.
21.如图,在?ABCD中,各内角的平分线分别相交于点E,F,G,H.
(1)求证:△ABG≌△CDE;
(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;
(3)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.
22.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?
并说明理由.
参考答案
1.D
2.B
3.A
4.B
5.C
6.B
7.A
8.C
9.A
10.C
11.矩形
5cm
12.①⑤
13.8
14.矩形
15.
16.9
17.解析:
解:∵Rt△ABE与Rt△DCF关于直线m对称,
∴AB=DC.
∵∠B=90°,∠C=90°,点B,E,F,C在同一条直线上,
∴AB∥CD.
∴四边形ABCD是平行四边形.
∵∠B=90°,∴平行四边形ABCD是矩形.
18.12.
解析:解:∵AE∥BC,BE∥AC,∴四边形AEDC是平行四边形,∴AE=CD.
在△ABC中,AB=AC,AD为BC边上的高,∴∠ADB=90°,BD=CD,∴BD=AE,∴平行四边形AEBD是矩形.
在Rt△ADC中,∠ADB=90°,AC=5,CD=BC=3,∴AD==4,∴四边形AEBD的面积为:BD?AD=CD?AD=3×4=12.
19.
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
又∵CF=AE,
∴BE=DF.
又∵BE∥DF,
∴四边形BFDE为平行四边形.
∵DE⊥AB,
∴∠DEB=90°.
∴四边形BFDE是矩形.
(2)∵四边形BFDE是矩形,
∴∠BFD=90°.∴∠BFC=90°.
在Rt△BFC中,由勾股定理,得BC===10.
∴AD=BC=10.
又∵DF=10,
∴AD=DF.
∴∠DAF=∠DFA.
∵AB∥CD,
∴∠DFA=∠FAB.
∴∠DAF=∠FAB.
∴AF是∠DAB的平分线.
20.(1)证明见解析;(2)
证明:在矩形ABCD中,AB=CD,
,
由折叠的性质可知:DE=CD,
,
∴AB=DE,
,
又∵,
∴△ABF≌△EDF(AAS)
(2)解:∵AD//BC,∴,由折叠的性质可知:
∴
∴BG=DG
设GC为,则BG=DG=8-x
在Rt△DCG中,由勾股定理可得:
解得:
21.(1)证明见解析;(2)矩形;(3).
解析:解:(1)∵GA平分∠BAD,EC平分∠BCD,∴∠BAG=∠BAD,∠DCE=∠DCB,∵?ABCD中,∠BAD=∠DCB,AB=CD,∴∠BAG=∠DCE,同理可得,∠ABG=∠CDE,在△ABG和△CDE中,∵∠BAG=∠DCE,AB=CD,∠ABG=∠CDE,∴△ABG≌△CDE(ASA);
(2)四边形EFGH是矩形.
证明:∵GA平分∠BAD,GB平分∠ABC,∴∠GAB=∠BAD,∠GBA=∠ABC,∵?ABCD中,∠DAB+∠ABC=180°,∴∠GAB+∠GBA=(∠DAB+∠ABC)=90°,即∠AGB=90°,同理可得,∠DEC=90°,∠AHD=90°=∠EHG,∴四边形EFGH是矩形;
(3)依题意得,∠BAG=∠BAD=30°,∵AB=6,∴BG=AB=3,AG==CE,∵BC=4,∠BCF=∠BCD=30°,∴BF=BC=2,CF=,∴EF=﹣=,GF=3﹣2=1,∴矩形EFGH的面积=EF×GF=.
22.试题解析:(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF==10,
∴OC=EF=5;
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
