北师大版八年级数学下册 6.2平行四边形判定课件 (第1课时 共20张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 6.2平行四边形判定课件 (第1课时 共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 474.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-22 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
北师大版八年级数学下册第六章6.2.1
平行四边形的判定(1)(2)
经历平行四边形判别条件的探索过程逐步掌握说理的基本方法;
掌握用平行四边形的定义判定一个四边形是平行四边形,探索并掌握平行四边形的判别条件;
在拼摆平行四边形的过程中,提升动手能力,积累数学活动经验。
一.学习目标
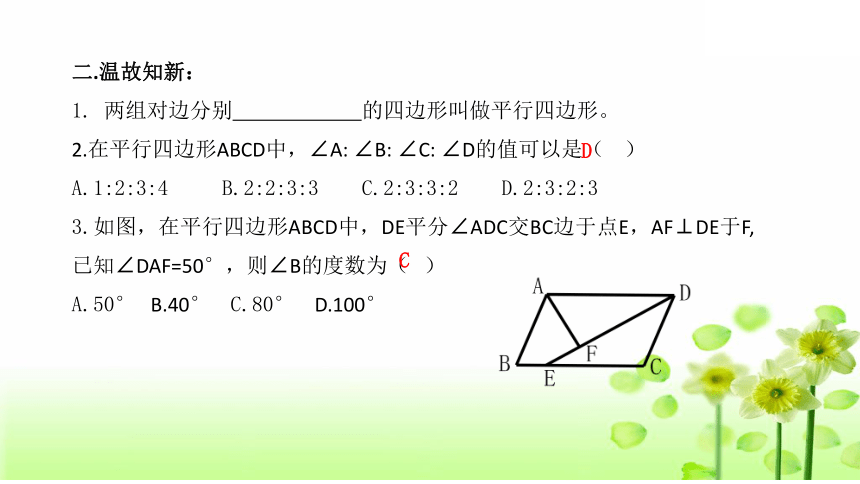
二.温故知新:
1.
两组对边分别
的四边形叫做平行四边形。
2.在平行四边形ABCD中,∠A:
∠B:
∠C:
∠D的值可以是(
)
A.1:2:3:4
B.2:2:3:3
C.2:3:3:2
D.2:3:2:3
3.如图,在平行四边形ABCD中,DE平分∠ADC交BC边于点E,AF⊥DE于F,已知∠DAF=50°,则∠B的度数为(
)
A.50°
B.40°
C.80°
D.100°
D
C
4.如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△DEF的周长为8,△CBF的周长为22,则平行四边形的周长为______.
30
根据题意得:EF=AE,BF=AB.
∵△FDE的周长为8,即DF+DE+EF=8,
∴DF+DE+AE=8,即DF+AD=8.
∵△FCB的周长为18,即FC+BC+BF=18,
∴FC+BC+AB=18,
∴平行四边形的周长为DF+AD+FC+BC+AB=8+22=30
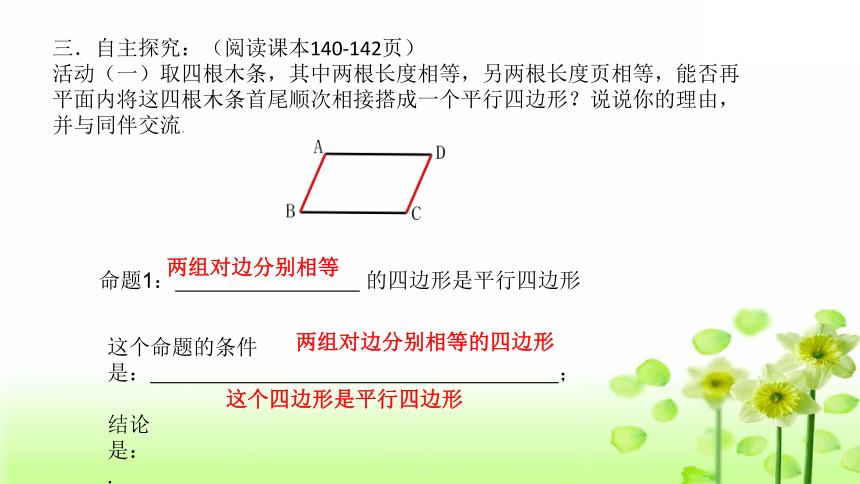
三.自主探究:(阅读课本140-142页)
活动(一)取四根木条,其中两根长度相等,另两根长度页相等,能否再平面内将这四根木条首尾顺次相接搭成一个平行四边形?说说你的理由,并与同伴交流。
命题1:
的四边形是平行四边形
两组对边分别相等
这个命题的条件是:
;
结论是:
.
两组对边分别相等的四边形
这个四边形是平行四边形
6
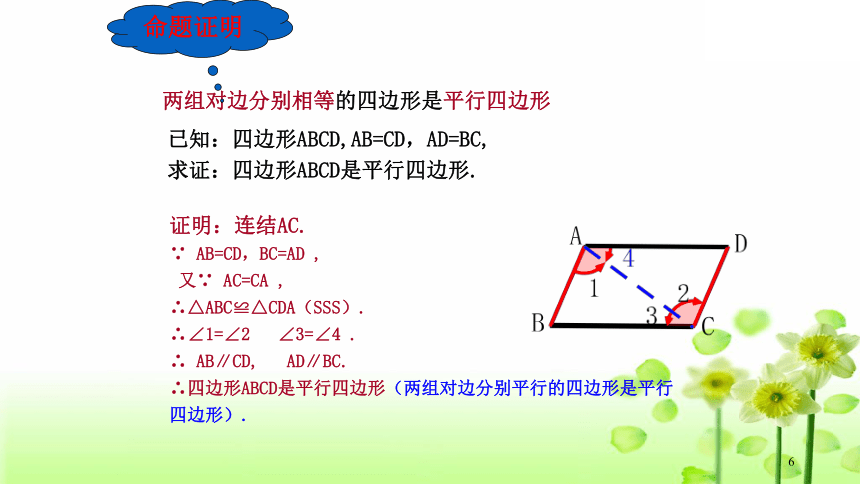
两组对边分别相等的四边形是平行四边形
已知:四边形ABCD,AB=CD,AD=BC,
求证:四边形ABCD是平行四边形.
证明:连结AC.
∵
AB=CD,BC=AD
,
又∵
AC=CA
,
∴△ABC≌△CDA(SSS).
∴∠1=∠2
∠3=∠4
.
∴
AB∥CD,
AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行
四边形).
命题证明
活动(二)议一议:
取两根长度相等的细木条,你能将它们摆放在一张纸上,使得这两根细木条的四个端点恰好是一个平行四边形的四个顶点吗?
如果四边形有一组对边相等,那么还需要添加什么条件。才能使它成为平行四边形?与同伴交流。
命题2:
的四边形是平行四边形。
添加条件是:这一组对边平行
一组对边平行且相等
这个命题的条件是:
;
结论是:
.
一组对边平行且相等的四边形
这个四边形是平行四边形
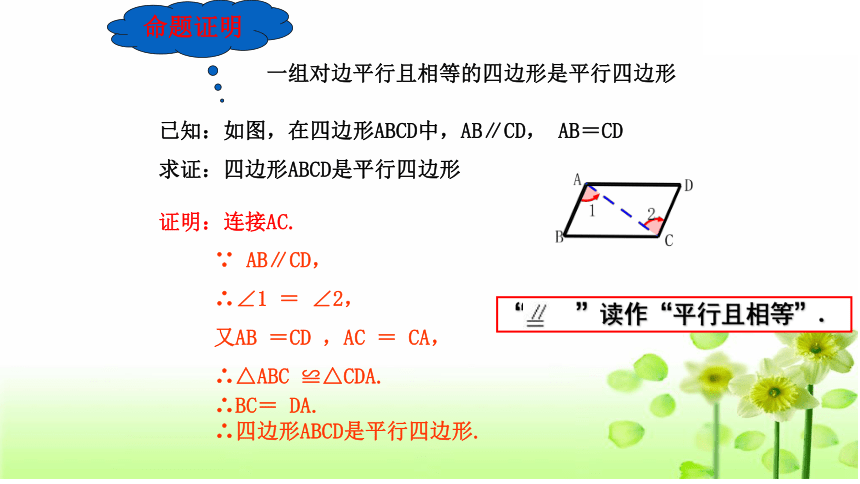
一组对边平行且相等的四边形是平行四边形
命题证明
已知:如图,在四边形ABCD中,AB∥CD,
AB=CD
求证:四边形ABCD是平行四边形
证明:连接AC.
∵
AB∥CD,
∴∠1
=
∠2,
又AB
=CD
,AC
=
CA,
∴△ABC
≌△CDA.
∴BC=
DA.
∴四边形ABCD是平行四边形.
“
”读作“平行且相等”.
四.小结:
平行四边形的判定方法有哪几种?
1.定义:
的四边形叫做平行四边形
几何语言:
两组对边分别平行
∵
AD∥BC,AB∥DC
∴
四边形ABCD是平行四边形
两组对边
分别平行
平行
四边形
性质
判定
定义既是性质,也是判定方法.
四.小结:
平行四边形的判定方法有哪几种?
2.判定定理(1):
的四边形是平行四边形;
几何语言:
3.判定定理(2):
的四边形是平行四边形;
几何语言:
一组对’边平行且相等
两组对边分别相等
∵
AD=BC,AB=DC
∴
四边形ABCD是平行四边形
∵
AD∥BC,AD=BC
∴
四边形ABCD是平行四边形
例1:已知:如图,E,F分别是
平行四边形ABCD
的边AD,BC的中点。
求证:BE=DF.
D
F
E
C
B
A
证明:方法一
∵四边形ABCD是平行四边形,
∴AB∥CD
(平行四边形的定义)
AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED
BF.
//
﹦
∴四边形EBFD是平行四边形(一组对边
平行并且相等的四边形是平行四边形)。
∴BE=DF(平行四边形的对边分别相等)。
例1:已知:如图,E,F分别是
平行四边形ABCD
的边AD,BC的中点。求证:BE=DF.
D
F
E
C
B
A
证明:方法二
∵四边形ABCD是平行四边形,
∴∠A=∠C
(平行四边形的对角分别相等),
AB=CD,AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴AE=CF
∴△ABE≌△CDF(SAS)
∴BE=DF
例2.如图,在平行四边形ABCD中,AF=CH,DE=BG,求证:四边形EFGH是平行四边形。
证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=BC,
∵DE=BG,
∴AE=CG,
在△AEF与△CGH中,
FB=DH,
∠A=∠C,
AE=CG
∴△AEF≌△CGH(SAS),
∴EF=GH,
同理可证:EH=FG,
∴四边形EFGH是平行四边形.
五.随堂练习:
1.用两根长40cm的木条作为四边形的一组对边,再用两根长50cm的木条作为四边形的另一组对边,拼成的一个四边形是
,其根据是
.
2.如图,△ABC≌△A’B’C’,点B,C’,C,B’在同一条直线上,且B与B’不重合,则以点A,B,A’,B’为顶点的四边形一定是
,其根据是
.
平行四边形
平行四边形
两组对边分别相等的四边形是
平行四边形
一组对’边平行且相等的四边形是
平行四边形
3.如图,线段AD是线段BC经过平移得到的,分别连接AB,CD,四边形ABCD是平行四边形吗?请说明理由。
解:四边形ABCD是平行四边形
理由:由平移得AD=BC,AD//BC
所以四边形ABCD是平行四边形
4.
如图,AB
=DC=EF,
AD=BC,DE=CF,则图中有哪些互相平行的线段?
请说明理由.
解:AB//CD//EF,AD//BC,DE//CF
理由:∵
AB=CD,AD=BC
∴四边形ABCD是平行四边形
∴AB//CD,AD//BC
∵
DC=EF,DE=CF
∴四边形CDE是平行四边形
∴DE//CF,CD//EF
1.已知:平行四边形ABCD中,E,F分别在边BC,DA上,且AF=CE。求证:四边形AECF是平行四边形
思考:
1.你还有其他的证法吗?
2.哪种方法比较简便呢?
B
C
D
A
F
E
证明:
∴AD∥CB,即AF∥CE.
∵
AF=CE,
∴四边形AECF是平行四边形.
∵四边形ABCD是平行四边形,
六.当堂检测
2.如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.求证:四边形ADEF是平行四边形.
证明:∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE;
∵BE=AF,
∴AF=DE;
∴四边形ADEF是平行四边形;
六.当堂检测:
1.在四边形ABCD中:①AB//CD;②AD//BC;③AB=CD;④AD=BC.从以上条件中选择两个条件,使四边形ABCD为平行四边形的选法共有(
)
A.3种
B.4种
C.5种
D.6种
B
如图所示:
①以AC为对角线,可以画出?AFCB,F(-3,1);
②以AB为对角线,可以画出?ACBE,E(1,-1);
③以BC为对角线,可以画出?ACDB,D(3,1);
故选:B.
2.如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点不能作为平行四边形第四个顶点的是(
)
A.(3,1)
B.(-4,1)
C.(1,-1)
D.(-3,1)
B
北师大版八年级数学下册第六章6.2.1
平行四边形的判定(1)(2)
经历平行四边形判别条件的探索过程逐步掌握说理的基本方法;
掌握用平行四边形的定义判定一个四边形是平行四边形,探索并掌握平行四边形的判别条件;
在拼摆平行四边形的过程中,提升动手能力,积累数学活动经验。
一.学习目标
二.温故知新:
1.
两组对边分别
的四边形叫做平行四边形。
2.在平行四边形ABCD中,∠A:
∠B:
∠C:
∠D的值可以是(
)
A.1:2:3:4
B.2:2:3:3
C.2:3:3:2
D.2:3:2:3
3.如图,在平行四边形ABCD中,DE平分∠ADC交BC边于点E,AF⊥DE于F,已知∠DAF=50°,则∠B的度数为(
)
A.50°
B.40°
C.80°
D.100°
D
C
4.如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△DEF的周长为8,△CBF的周长为22,则平行四边形的周长为______.
30
根据题意得:EF=AE,BF=AB.
∵△FDE的周长为8,即DF+DE+EF=8,
∴DF+DE+AE=8,即DF+AD=8.
∵△FCB的周长为18,即FC+BC+BF=18,
∴FC+BC+AB=18,
∴平行四边形的周长为DF+AD+FC+BC+AB=8+22=30
三.自主探究:(阅读课本140-142页)
活动(一)取四根木条,其中两根长度相等,另两根长度页相等,能否再平面内将这四根木条首尾顺次相接搭成一个平行四边形?说说你的理由,并与同伴交流。
命题1:
的四边形是平行四边形
两组对边分别相等
这个命题的条件是:
;
结论是:
.
两组对边分别相等的四边形
这个四边形是平行四边形
6
两组对边分别相等的四边形是平行四边形
已知:四边形ABCD,AB=CD,AD=BC,
求证:四边形ABCD是平行四边形.
证明:连结AC.
∵
AB=CD,BC=AD
,
又∵
AC=CA
,
∴△ABC≌△CDA(SSS).
∴∠1=∠2
∠3=∠4
.
∴
AB∥CD,
AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行
四边形).
命题证明
活动(二)议一议:
取两根长度相等的细木条,你能将它们摆放在一张纸上,使得这两根细木条的四个端点恰好是一个平行四边形的四个顶点吗?
如果四边形有一组对边相等,那么还需要添加什么条件。才能使它成为平行四边形?与同伴交流。
命题2:
的四边形是平行四边形。
添加条件是:这一组对边平行
一组对边平行且相等
这个命题的条件是:
;
结论是:
.
一组对边平行且相等的四边形
这个四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
命题证明
已知:如图,在四边形ABCD中,AB∥CD,
AB=CD
求证:四边形ABCD是平行四边形
证明:连接AC.
∵
AB∥CD,
∴∠1
=
∠2,
又AB
=CD
,AC
=
CA,
∴△ABC
≌△CDA.
∴BC=
DA.
∴四边形ABCD是平行四边形.
“
”读作“平行且相等”.
四.小结:
平行四边形的判定方法有哪几种?
1.定义:
的四边形叫做平行四边形
几何语言:
两组对边分别平行
∵
AD∥BC,AB∥DC
∴
四边形ABCD是平行四边形
两组对边
分别平行
平行
四边形
性质
判定
定义既是性质,也是判定方法.
四.小结:
平行四边形的判定方法有哪几种?
2.判定定理(1):
的四边形是平行四边形;
几何语言:
3.判定定理(2):
的四边形是平行四边形;
几何语言:
一组对’边平行且相等
两组对边分别相等
∵
AD=BC,AB=DC
∴
四边形ABCD是平行四边形
∵
AD∥BC,AD=BC
∴
四边形ABCD是平行四边形
例1:已知:如图,E,F分别是
平行四边形ABCD
的边AD,BC的中点。
求证:BE=DF.
D
F
E
C
B
A
证明:方法一
∵四边形ABCD是平行四边形,
∴AB∥CD
(平行四边形的定义)
AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED
BF.
//
﹦
∴四边形EBFD是平行四边形(一组对边
平行并且相等的四边形是平行四边形)。
∴BE=DF(平行四边形的对边分别相等)。
例1:已知:如图,E,F分别是
平行四边形ABCD
的边AD,BC的中点。求证:BE=DF.
D
F
E
C
B
A
证明:方法二
∵四边形ABCD是平行四边形,
∴∠A=∠C
(平行四边形的对角分别相等),
AB=CD,AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴AE=CF
∴△ABE≌△CDF(SAS)
∴BE=DF
例2.如图,在平行四边形ABCD中,AF=CH,DE=BG,求证:四边形EFGH是平行四边形。
证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=BC,
∵DE=BG,
∴AE=CG,
在△AEF与△CGH中,
FB=DH,
∠A=∠C,
AE=CG
∴△AEF≌△CGH(SAS),
∴EF=GH,
同理可证:EH=FG,
∴四边形EFGH是平行四边形.
五.随堂练习:
1.用两根长40cm的木条作为四边形的一组对边,再用两根长50cm的木条作为四边形的另一组对边,拼成的一个四边形是
,其根据是
.
2.如图,△ABC≌△A’B’C’,点B,C’,C,B’在同一条直线上,且B与B’不重合,则以点A,B,A’,B’为顶点的四边形一定是
,其根据是
.
平行四边形
平行四边形
两组对边分别相等的四边形是
平行四边形
一组对’边平行且相等的四边形是
平行四边形
3.如图,线段AD是线段BC经过平移得到的,分别连接AB,CD,四边形ABCD是平行四边形吗?请说明理由。
解:四边形ABCD是平行四边形
理由:由平移得AD=BC,AD//BC
所以四边形ABCD是平行四边形
4.
如图,AB
=DC=EF,
AD=BC,DE=CF,则图中有哪些互相平行的线段?
请说明理由.
解:AB//CD//EF,AD//BC,DE//CF
理由:∵
AB=CD,AD=BC
∴四边形ABCD是平行四边形
∴AB//CD,AD//BC
∵
DC=EF,DE=CF
∴四边形CDE是平行四边形
∴DE//CF,CD//EF
1.已知:平行四边形ABCD中,E,F分别在边BC,DA上,且AF=CE。求证:四边形AECF是平行四边形
思考:
1.你还有其他的证法吗?
2.哪种方法比较简便呢?
B
C
D
A
F
E
证明:
∴AD∥CB,即AF∥CE.
∵
AF=CE,
∴四边形AECF是平行四边形.
∵四边形ABCD是平行四边形,
六.当堂检测
2.如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.求证:四边形ADEF是平行四边形.
证明:∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE;
∵BE=AF,
∴AF=DE;
∴四边形ADEF是平行四边形;
六.当堂检测:
1.在四边形ABCD中:①AB//CD;②AD//BC;③AB=CD;④AD=BC.从以上条件中选择两个条件,使四边形ABCD为平行四边形的选法共有(
)
A.3种
B.4种
C.5种
D.6种
B
如图所示:
①以AC为对角线,可以画出?AFCB,F(-3,1);
②以AB为对角线,可以画出?ACBE,E(1,-1);
③以BC为对角线,可以画出?ACDB,D(3,1);
故选:B.
2.如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点不能作为平行四边形第四个顶点的是(
)
A.(3,1)
B.(-4,1)
C.(1,-1)
D.(-3,1)
B
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
