垂直关系的判定(一)
图片预览

文档简介
课题:垂直关系的判定(一)
---------直线与平面垂直的判定
学习目标
1、能准确说出线面垂直定义及线面垂直判定定理中所需条件,并能用文字语言、符号语言、图形语言进行表达.
2、能利用判定定理证明或判断具体图形中的线面垂直.
3、通过对定理的学习,培养和发展空间想象能力、推理论证能力、运用图形语言进行交流的能力、几何直观能力,逐步学习运用数学语言进行推理和论证,培养严谨的科学态度.
学习重点、难点
重点:直线与平面垂直关系的判定定理.
难点:对直线和平面垂直判定定理的理解.
学习过程
一、课前准备
复习1.在同一个平面内有哪些方法可以判定两条直线垂直?
复习2.若空间两条直线垂直,这两条直线一定相交吗?
二、新课导学
学习探究
(预习教材P35~P36,找出疑惑之处,并尝试解决以下问题)
1、直线与平面垂直的定义.(用文字语言、符号语言表示)
2、直线与平面垂直的判定定理.(分别用三种语言描述)
3、判断下面的说法是否正确:
(1)若直线与平面内的一条直线垂直,则⊥.( )
(2)若直线与平面内的两条直线垂直,则⊥.( )
(3)若直线与平面内的无数条直线垂直,则⊥.( )
(4)若直线与平面内的所有直线垂直,则⊥.( )
(5)若直线⊥平面,则与内的任一直线垂直.( )
(6)若直线与平面不垂直,则与内的任一直线都不垂直.( )
(7)若直线∥直线,⊥平面,则⊥.( )
典型例题
题型一 直线和平面垂直判定定理的应用
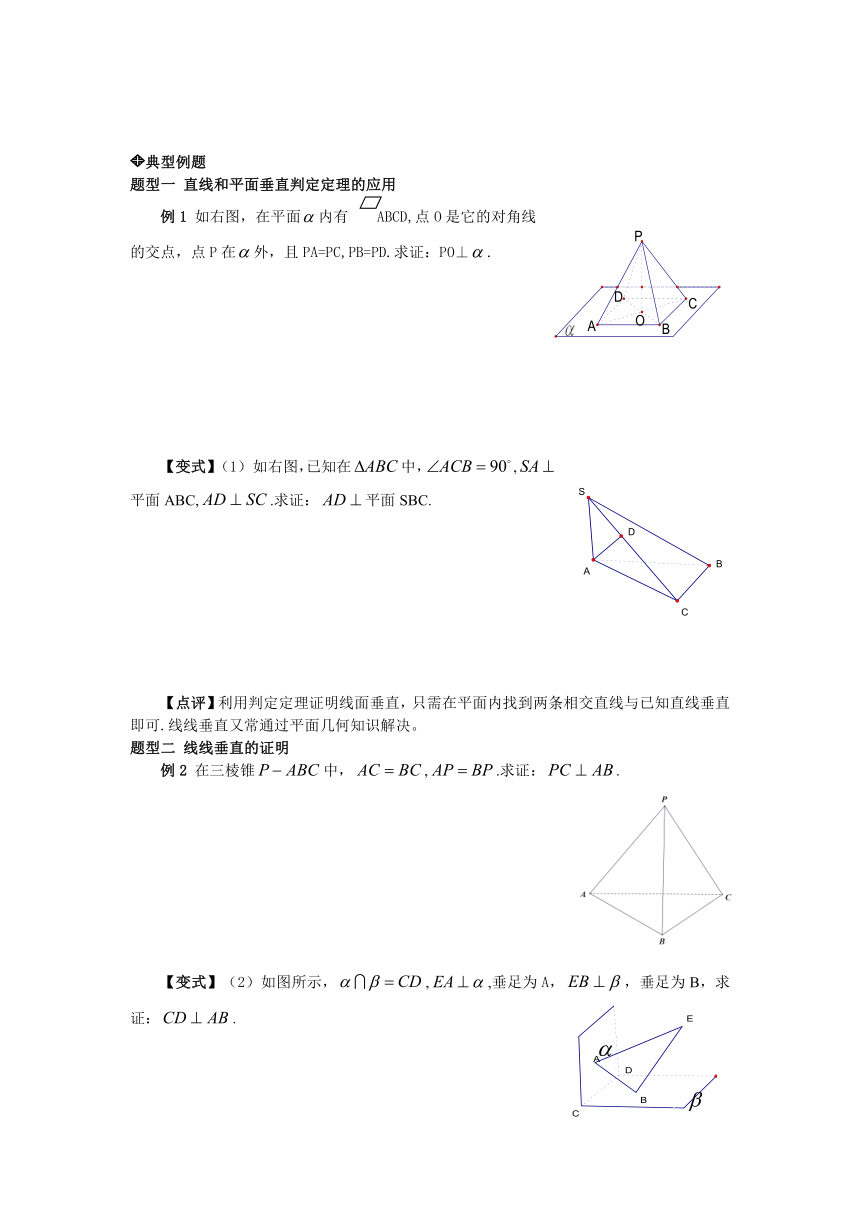
例1 如右图,在平面内有 ABCD,点O是它的对角线的交点,点P在外,且PA=PC,PB=PD.求证:PO⊥.
【变式】 (1) 如右图,已知在中,,平面ABC,.求证:平面SBC.
【点评】利用判定定理证明线面垂直,只需在平面内找到两条相交直线与已知直线垂直即可.线线垂直又常通过平面几何知识解决。
题型二 线线垂直的证明
例2 在三棱锥中,,.求证:.
【变式】(2)如图所示,,,垂足为A,,垂足为B,求证:.
小结:要证线线垂直可以先证明线面垂直。
三、总结提升
学习小结
1.线面垂直的定义也可以用来判定线线垂直.
2.线面垂直的判定方法有:
(1)利用定义,证明这条直线和平面内的任一直线垂直;
(2)利用判定定理,证明这条直线和平面内的两条相交直线垂直;
(3)利用平行关系的传递性:若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.
知识拓展
1.若直线∥直线,⊥直线,则;
2.若直线∥直线,⊥平面,则;
3.若平面∥平面,直线,则;
4.过空间一点作已知平面的垂线有且只有一条;
5.过空间一点作已知直线的垂面有且只有一个.
学习评价
当堂检测
(时间:5分钟,满分:10分)计分:
1、 若、表示直线,表示平面:⊥,⊥∥;∥,∥∥;∥,⊥⊥;⊥,⊥.其中正确命题的个数是( )
A.4个 B.3个
C.2个 D.1个
2、与不共线的三点距离都相等的点的个数是 .
3、如果一条直线垂直于一个平面内的:三角形的两条边;梯形的两条边;圆的两条直径. 其中能保证这条直线和平面垂直的是 .
4、过空间一点和已知平面垂直的直线有_ ___条,垂直的平面有__ ___个;过空间一点和已知直线垂直的直线有___ __条,垂直的平面有_ ____个.
5、已知四面体ABCD中,BC=AC,BD=AD,BECD于E,求证:CD平面ABE.
课后演练
1、 教室内有一直尺,无论怎样放置,在地面总有直线和直尺所在的直线( )
A.平行 B.垂直
C.相交 D.异面
2、m,n是空间中两条直线,是空间中两个平面,下列条件能使m成立的是( )
A. , B.
C. D.
3、如图,如果MC菱形ABCD所在平面,那么MA与BD的位置关系是( )
A. 平行 B. 垂直相交
C. 异面且垂直 D. 相交但不垂直
4、共点的三条直线OA、OB、OC 两两互相垂直,则OA与BC的关系是 .
5、空间与两定点距离相等的点有_________个,这些点可构成______________;
空间与不共线的三点距离都相等的点有 个,这些点可构成 .
6、在正方体ABCD-A’B’C’D’中,求证:A’C⊥BD,平面.
---------直线与平面垂直的判定
学习目标
1、能准确说出线面垂直定义及线面垂直判定定理中所需条件,并能用文字语言、符号语言、图形语言进行表达.
2、能利用判定定理证明或判断具体图形中的线面垂直.
3、通过对定理的学习,培养和发展空间想象能力、推理论证能力、运用图形语言进行交流的能力、几何直观能力,逐步学习运用数学语言进行推理和论证,培养严谨的科学态度.
学习重点、难点
重点:直线与平面垂直关系的判定定理.
难点:对直线和平面垂直判定定理的理解.
学习过程
一、课前准备
复习1.在同一个平面内有哪些方法可以判定两条直线垂直?
复习2.若空间两条直线垂直,这两条直线一定相交吗?
二、新课导学
学习探究
(预习教材P35~P36,找出疑惑之处,并尝试解决以下问题)
1、直线与平面垂直的定义.(用文字语言、符号语言表示)
2、直线与平面垂直的判定定理.(分别用三种语言描述)
3、判断下面的说法是否正确:
(1)若直线与平面内的一条直线垂直,则⊥.( )
(2)若直线与平面内的两条直线垂直,则⊥.( )
(3)若直线与平面内的无数条直线垂直,则⊥.( )
(4)若直线与平面内的所有直线垂直,则⊥.( )
(5)若直线⊥平面,则与内的任一直线垂直.( )
(6)若直线与平面不垂直,则与内的任一直线都不垂直.( )
(7)若直线∥直线,⊥平面,则⊥.( )
典型例题
题型一 直线和平面垂直判定定理的应用
例1 如右图,在平面内有 ABCD,点O是它的对角线的交点,点P在外,且PA=PC,PB=PD.求证:PO⊥.
【变式】 (1) 如右图,已知在中,,平面ABC,.求证:平面SBC.
【点评】利用判定定理证明线面垂直,只需在平面内找到两条相交直线与已知直线垂直即可.线线垂直又常通过平面几何知识解决。
题型二 线线垂直的证明
例2 在三棱锥中,,.求证:.
【变式】(2)如图所示,,,垂足为A,,垂足为B,求证:.
小结:要证线线垂直可以先证明线面垂直。
三、总结提升
学习小结
1.线面垂直的定义也可以用来判定线线垂直.
2.线面垂直的判定方法有:
(1)利用定义,证明这条直线和平面内的任一直线垂直;
(2)利用判定定理,证明这条直线和平面内的两条相交直线垂直;
(3)利用平行关系的传递性:若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.
知识拓展
1.若直线∥直线,⊥直线,则;
2.若直线∥直线,⊥平面,则;
3.若平面∥平面,直线,则;
4.过空间一点作已知平面的垂线有且只有一条;
5.过空间一点作已知直线的垂面有且只有一个.
学习评价
当堂检测
(时间:5分钟,满分:10分)计分:
1、 若、表示直线,表示平面:⊥,⊥∥;∥,∥∥;∥,⊥⊥;⊥,⊥.其中正确命题的个数是( )
A.4个 B.3个
C.2个 D.1个
2、与不共线的三点距离都相等的点的个数是 .
3、如果一条直线垂直于一个平面内的:三角形的两条边;梯形的两条边;圆的两条直径. 其中能保证这条直线和平面垂直的是 .
4、过空间一点和已知平面垂直的直线有_ ___条,垂直的平面有__ ___个;过空间一点和已知直线垂直的直线有___ __条,垂直的平面有_ ____个.
5、已知四面体ABCD中,BC=AC,BD=AD,BECD于E,求证:CD平面ABE.
课后演练
1、 教室内有一直尺,无论怎样放置,在地面总有直线和直尺所在的直线( )
A.平行 B.垂直
C.相交 D.异面
2、m,n是空间中两条直线,是空间中两个平面,下列条件能使m成立的是( )
A. , B.
C. D.
3、如图,如果MC菱形ABCD所在平面,那么MA与BD的位置关系是( )
A. 平行 B. 垂直相交
C. 异面且垂直 D. 相交但不垂直
4、共点的三条直线OA、OB、OC 两两互相垂直,则OA与BC的关系是 .
5、空间与两定点距离相等的点有_________个,这些点可构成______________;
空间与不共线的三点距离都相等的点有 个,这些点可构成 .
6、在正方体ABCD-A’B’C’D’中,求证:A’C⊥BD,平面.
