人教版九年级下册数学 28.1 锐角三角函数——余弦和正切课件(共20张PPT)
文档属性
| 名称 | 人教版九年级下册数学 28.1 锐角三角函数——余弦和正切课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 819.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-22 17:44:44 | ||
图片预览




文档简介
(共20张PPT)
28.1锐角三角函数—余弦与正切(人民教育出版社九年级数学下册)
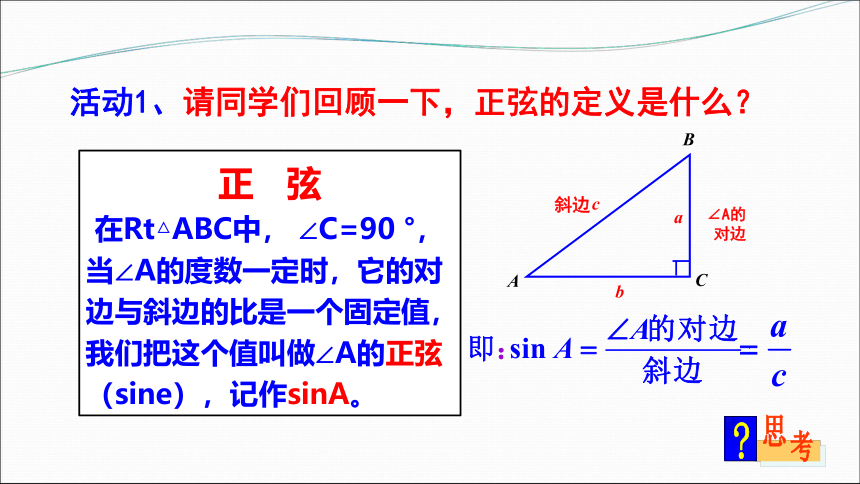
正
弦
在Rt△ABC中,
∠C=90
°,
当∠A的度数一定时,它的对边与斜边的比是一个固定值,我们把这个值叫做∠A的正弦(sine),记作sinA。
即:
∠A的
对边
活动1、请同学们回顾一下,正弦的定义是什么?
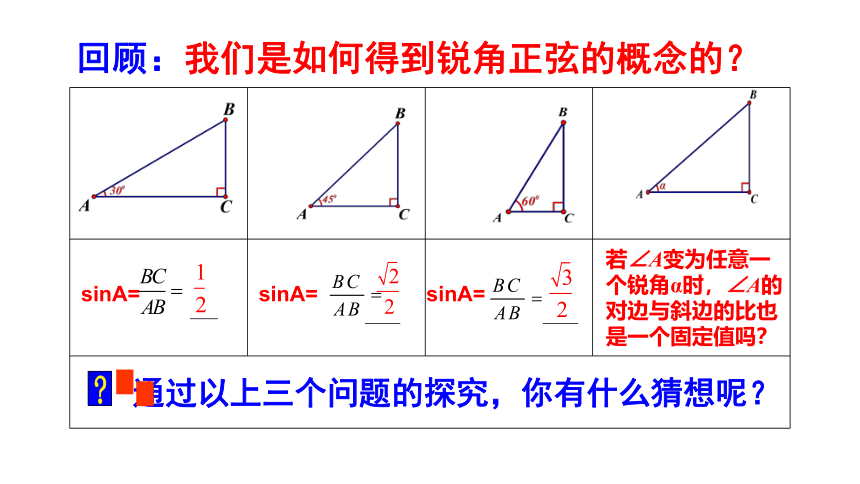
通过以上三个问题的探究,你有什么猜想呢?
sinA=
sinA=
sinA=
回顾:我们是如何得到锐角正弦的概念的?
这就是说:在直角三角形中,当锐角A
的度数一定时,无论这个直角三角形的大小如何,
∠A的对边与斜边的比是一个固定值.我们把这个值叫做∠A的正弦。
证明:
∵
∠C=
∠C
′
=90
°
∠A=
∠A
′
∴Rt
△ABC
∽Rt
△A
′
B
′
C
′
学习目标:
1.理解锐角余弦、正切的概念,掌握
其表示方法.
2.能运用三角函数概念进行计算.
3.归纳探究问题的一般思路.
任务一、在Rt△ABC
中,∠C=90°,当∠A的度数确定时,∠A
的邻边与斜边比是否是一个固定值呢?为什么?
任务二、在Rt△ABC
中,∠C=90°,当∠A的度数确定时,∠A
的对边与邻边的比是否是一个固定值呢?为什么?
请类比正弦的情况,利用相似三角形的知识进行探究.
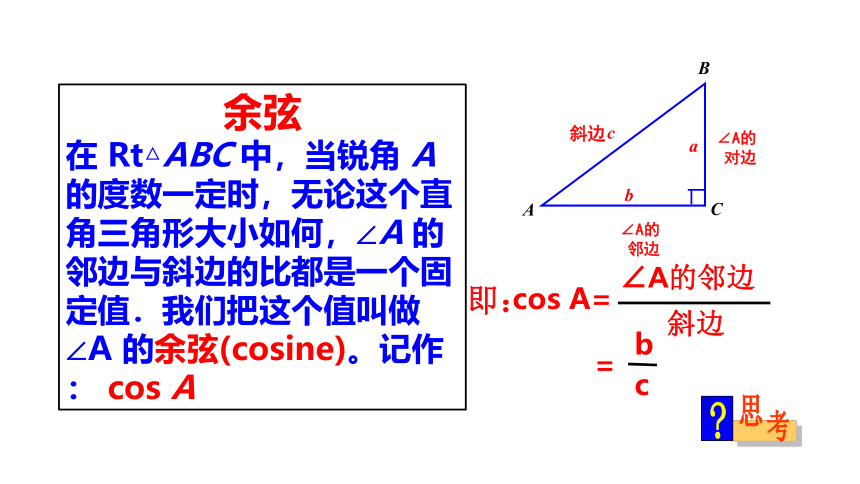
即:
∠A的
对边
余弦
在
Rt△ABC
中,当锐角
A
的度数一定时,无论这个直角三角形大小如何,∠A
的邻边与斜边的比都是一个固定值.我们把这个值叫做∠A
的余弦(cosine)。记作:
cos
A
cos
A=
∠A的邻边
斜边
∠A的
邻边
=
b
c
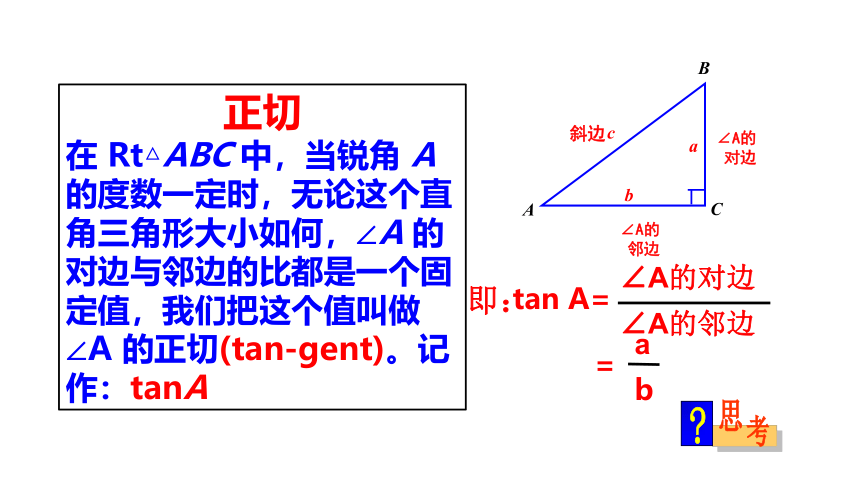
即:
∠A的
对边
正切
在
Rt△ABC
中,当锐角
A
的度数一定时,无论这个直角三角形大小如何,∠A
的对边与邻边的比都是一个固定值,我们把这个值叫做∠A
的正切(tan-gent)。记作:tanA
tan
A=
∠A的对边
∠A的
邻边
=
a
b
∠A的邻边
竖直高度
水平宽度
倾斜角
议一议:
梯子AB的倾斜角与sinA有什么关系?与cosA有什么关系?与tanA呢?
A
C
B
竖直高度
水平宽度
A
B
C
议一议:
梯子AB的倾斜角与sinA有什么关系?与cosA有什么关系?与tanA呢?
竖直高度
水平宽度
A
B
C
议一议:
梯子AB的倾斜角与sinA有什么关系?与cosA有什么关系?与tanA呢?
竖直高度
水平宽度
A
C
B
议一议:
梯子AB的倾斜角与sinA有什么关系?
与cosA有什么关系?与tanA呢?
通过上面的探究可以知道,当锐角A发生变化时,∠A的正弦值sinA随之发生变化。对于锐角A的每一个值,sinA有唯一的值和它对应,所以sinA是A的函数.同样地,cosA,tanA也是A的函数。
∠A的正弦、余弦、正切都是∠A的锐角三角函数
例题解析:如图,在Rt△ABC中,∠C=90°,BC=6cm
,AB=10
cm,求sinA、cosA和tanA的值.
10
归纳:求sinA就是要确定∠A的对边与斜边的比;求cosA就是要确定∠A的邻边与斜边的比;求tanA就是要确定∠A的对边与邻边的比
。
1.
分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.你发现什么规律?
解:由勾股定理:
小试牛刀:
规
律
sinA=cosB
cosA=sinB
tanA
·tanB=1
2.
在Rt△ABC中,如果各边长都扩大2倍,那么锐角A的正
弦值、余弦值和正切值有什么变化?
解:设各边长分别为a、b、c,∠A的三个三角函数分别为
则扩大2倍后三边分别为2a、2b、2c
3.如图:P是∠的边OA上一点,且P点的坐标为(3,4),则cosα
、tanα的值.
cosα=
tanα=
4.如图,
∠ACB=90°CD⊥AB.
tan∠ACD
=
tanB=
通过本节课你学到了那些知识?你还有哪些收获呢?请整理一下,发表自己的见解!
1、理解了余弦、正切的概念.
2、数形结合的方法,构造直角三角形的意识.
3、类比的数学思想方法.
……
1.教科书第65页练习1(2).
2.教科书69页综合运用6、7.
3.
探究锐角A的三个三角函数之间的关系.
数学源于对生活的热心,请不要停止探索的步伐!
28.1锐角三角函数—余弦与正切(人民教育出版社九年级数学下册)
正
弦
在Rt△ABC中,
∠C=90
°,
当∠A的度数一定时,它的对边与斜边的比是一个固定值,我们把这个值叫做∠A的正弦(sine),记作sinA。
即:
∠A的
对边
活动1、请同学们回顾一下,正弦的定义是什么?
通过以上三个问题的探究,你有什么猜想呢?
sinA=
sinA=
sinA=
回顾:我们是如何得到锐角正弦的概念的?
这就是说:在直角三角形中,当锐角A
的度数一定时,无论这个直角三角形的大小如何,
∠A的对边与斜边的比是一个固定值.我们把这个值叫做∠A的正弦。
证明:
∵
∠C=
∠C
′
=90
°
∠A=
∠A
′
∴Rt
△ABC
∽Rt
△A
′
B
′
C
′
学习目标:
1.理解锐角余弦、正切的概念,掌握
其表示方法.
2.能运用三角函数概念进行计算.
3.归纳探究问题的一般思路.
任务一、在Rt△ABC
中,∠C=90°,当∠A的度数确定时,∠A
的邻边与斜边比是否是一个固定值呢?为什么?
任务二、在Rt△ABC
中,∠C=90°,当∠A的度数确定时,∠A
的对边与邻边的比是否是一个固定值呢?为什么?
请类比正弦的情况,利用相似三角形的知识进行探究.
即:
∠A的
对边
余弦
在
Rt△ABC
中,当锐角
A
的度数一定时,无论这个直角三角形大小如何,∠A
的邻边与斜边的比都是一个固定值.我们把这个值叫做∠A
的余弦(cosine)。记作:
cos
A
cos
A=
∠A的邻边
斜边
∠A的
邻边
=
b
c
即:
∠A的
对边
正切
在
Rt△ABC
中,当锐角
A
的度数一定时,无论这个直角三角形大小如何,∠A
的对边与邻边的比都是一个固定值,我们把这个值叫做∠A
的正切(tan-gent)。记作:tanA
tan
A=
∠A的对边
∠A的
邻边
=
a
b
∠A的邻边
竖直高度
水平宽度
倾斜角
议一议:
梯子AB的倾斜角与sinA有什么关系?与cosA有什么关系?与tanA呢?
A
C
B
竖直高度
水平宽度
A
B
C
议一议:
梯子AB的倾斜角与sinA有什么关系?与cosA有什么关系?与tanA呢?
竖直高度
水平宽度
A
B
C
议一议:
梯子AB的倾斜角与sinA有什么关系?与cosA有什么关系?与tanA呢?
竖直高度
水平宽度
A
C
B
议一议:
梯子AB的倾斜角与sinA有什么关系?
与cosA有什么关系?与tanA呢?
通过上面的探究可以知道,当锐角A发生变化时,∠A的正弦值sinA随之发生变化。对于锐角A的每一个值,sinA有唯一的值和它对应,所以sinA是A的函数.同样地,cosA,tanA也是A的函数。
∠A的正弦、余弦、正切都是∠A的锐角三角函数
例题解析:如图,在Rt△ABC中,∠C=90°,BC=6cm
,AB=10
cm,求sinA、cosA和tanA的值.
10
归纳:求sinA就是要确定∠A的对边与斜边的比;求cosA就是要确定∠A的邻边与斜边的比;求tanA就是要确定∠A的对边与邻边的比
。
1.
分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.你发现什么规律?
解:由勾股定理:
小试牛刀:
规
律
sinA=cosB
cosA=sinB
tanA
·tanB=1
2.
在Rt△ABC中,如果各边长都扩大2倍,那么锐角A的正
弦值、余弦值和正切值有什么变化?
解:设各边长分别为a、b、c,∠A的三个三角函数分别为
则扩大2倍后三边分别为2a、2b、2c
3.如图:P是∠的边OA上一点,且P点的坐标为(3,4),则cosα
、tanα的值.
cosα=
tanα=
4.如图,
∠ACB=90°CD⊥AB.
tan∠ACD
=
tanB=
通过本节课你学到了那些知识?你还有哪些收获呢?请整理一下,发表自己的见解!
1、理解了余弦、正切的概念.
2、数形结合的方法,构造直角三角形的意识.
3、类比的数学思想方法.
……
1.教科书第65页练习1(2).
2.教科书69页综合运用6、7.
3.
探究锐角A的三个三角函数之间的关系.
数学源于对生活的热心,请不要停止探索的步伐!
