2019—2020学年人教版选修3-4 机械振动 单元检测试题4(解析版)
文档属性
| 名称 | 2019—2020学年人教版选修3-4 机械振动 单元检测试题4(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 242.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-21 17:58:21 | ||
图片预览




文档简介
机械振动
单元检测试题(解析版)
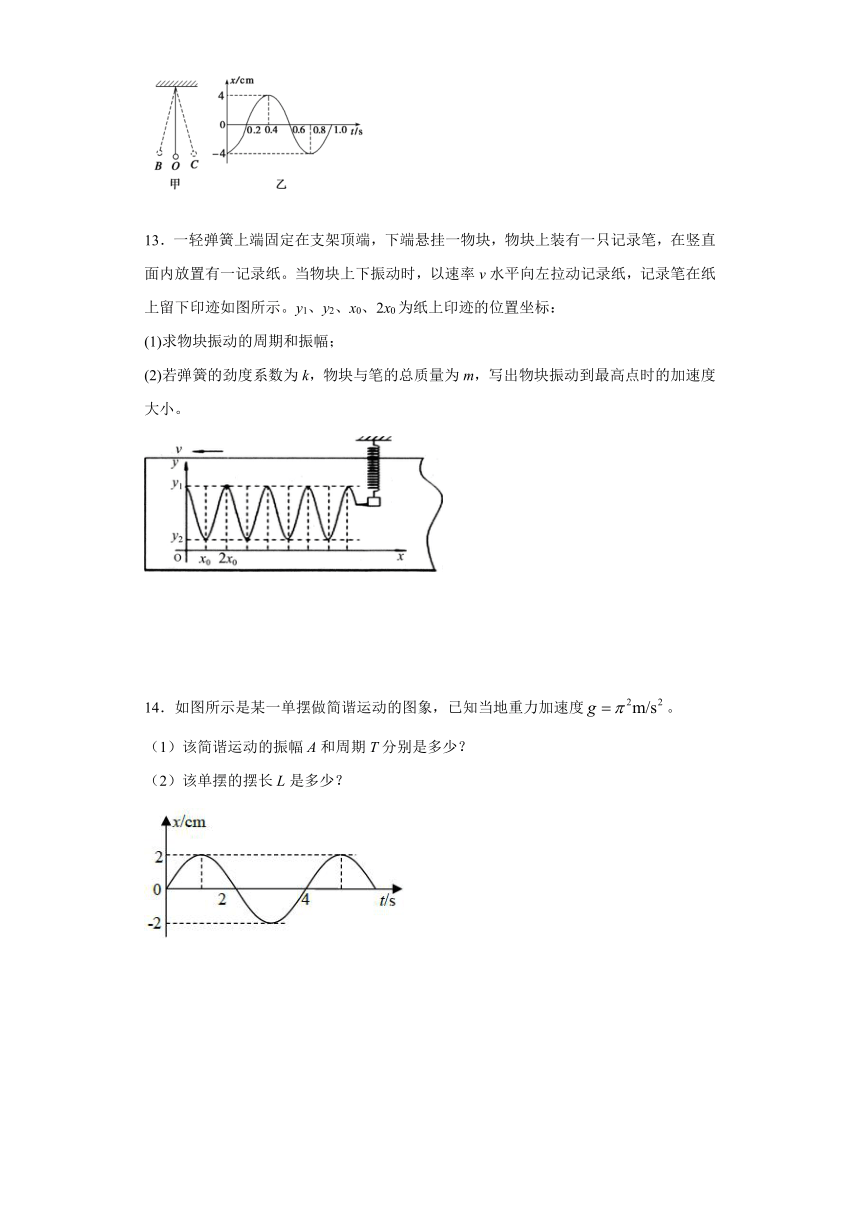
1.如图甲所示,水平的光滑杆上有一弹簧振子,振子以O点为平衡位置,在a、b两点之间做简谐运动,其振动图像如图乙所示。由振动图像可以得知( )
A.从t1到t2,振子正从O点向a点运动
B.在t=0时刻,振子的位置在a点
C.在t=t1时刻,振子的速度最大
D.在t=t2时刻,振子的加速度为零
2.如图所示,一单摆摆长为L,在悬点正下方0.19L处有一钉子。现将摆球向左拉开到A处,使摆角θ<5°,放手使其摆动,则此单摆的振动周期为( )
A.
B.
C.
D.
3.下列说法错误的是( )
A.在同一地点,单摆做简谐振动的周期的平方与其摆长成正比
B.弹簧振子做简谐振动时,振动系统的势能与动能之和保持不变
C.在同一地点,当摆长不变时,摆球质量越大,单摆做简谐振动的周期越小
D.系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率
4.如图所示,一根轻质弹簧上端固定在天花板,下端连接一个可视为质点的物块,不计空气阻力,物块沿竖直方向以O点为中心点,在C、D之间做周期为T的简谐运动。已知在初时刻t1时物块的动量为p、动能为Ek。下列说法正确的是( )
A.当物块通过O点时,其回复力最小
B.物块运动至C点时,其加速度最小
C.如果在末时刻t2时刻物块的动量也为p,则从t1到t2之间的时间间隔的最小值为T
D.如果在末时刻t2时刻物块的动能也为Ek,则从t1到t2之间的时间间隔的最小值为T
5.做简谐运动的物体,在不同时刻通过同一确定位置时可能不相同的物理量是(
)
A.加速度
B.动能
C.速度
D.位移
6.如图,O点为弹簧振子的平衡位置,小球在B、C间做无摩擦的往复运动。在小球从B运动到O的过程中,小球的(
)
A.速度不断增大,加速度不断增大
B.速度不断减小,加速度不断增大
C.速度不断增大,加速度不断减小
D.速度不断减小,加速度不断减小
7.某质点的振动图象如图所示,根据图象可知( )
A.质点振动的振幅为
B.质点振动的周期为
C.t=1s时,质点有负的最大位移
D.t=2s时,质点的运动速度为零
8.如图所示,在一根张紧的水平绳上挂有
5
个单摆,其中
b
摆球质量最大,其余
4
个摆球质量相等,摆长关系为
Lc>Lb=Ld>La>Le,现将
b
摆垂直纸面向里拉开一微小角度后释放,经过一段时间后,其余各摆均振动起来并达到稳定,下列叙述正确的是(
)
A.4
个单摆的周期
Tc>Td>Ta>Te
B.4
个单摆的频率
fa=fc=fd=fe
C.4
个单摆的振幅
Aa=Ac=Ad=Ae
D.4
个单摆中
c
摆的振幅最大
9.一质点做简谐运动,其位移x与时间t的关系图象如图所示,由图可知( )
A.质点振动的频率是4Hz,振幅是2cm
B.质点经过5s通过的路程总共是10cm
C.质点在t=2s和t=4s两时刻的位移相等
D.质点做简谐运动的表达式为
10.如图所示.曲轴上挂一个弹簧振子,转动摇把,曲轴可带动弹簧振子上、下振动.开始时不转动摇把,让振子自由振动,测得其频率为2Hz.现匀速转动摇把,转速为240r/min.则:(
)
A.当振子稳定振动时,它的振动周期是0.5s
B.当振子稳定振动时,它的振动频率是4Hz
C.当转速增大时,弹簧振子的振幅增大
D.当转速减小时,弹簧振子的振幅增大
11.一弹簧振子的位移x随时间t变化的关系式为x=0.1sin(2.5πt+),位移x的单位为m,时间t的单位为s。则弹簧振子的周期为_____s;弹簧振子的振动初相位_______;在t=0.4s时,振子的位移_____m,振子的加速度是_______(填最大或最小)。在t=0.4s到t=0.6s时间段内振子的动能________(填增加或减小)。
12.如图甲是一个单摆振动的情形,O是它的平衡位置,B、C是摆球所能到达的最远位置。设向右为正方向,图乙是这个单摆的振动图象。根据图象可得,单摆振动的频率是_______Hz;开始时摆球在______位置;若当地的重力加速度为10
m/s2,试求这个摆的摆长是______m。
13.一轻弹簧上端固定在支架顶端,下端悬挂一物块,物块上装有一只记录笔,在竖直面内放置有一记录纸。当物块上下振动时,以速率v水平向左拉动记录纸,记录笔在纸上留下印迹如图所示。y1、y2、x0、2x0为纸上印迹的位置坐标:
(1)求物块振动的周期和振幅;
(2)若弹簧的劲度系数为k,物块与笔的总质量为m,写出物块振动到最高点时的加速度大小。
14.如图所示是某一单摆做简谐运动的图象,已知当地重力加速度。
(1)该简谐运动的振幅A和周期T分别是多少?
(2)该单摆的摆长L是多少?
15.如图所示,在质量M=5kg的无下底的木箱顶部用一轻弹簧悬挂质量分别为mA=1kg、mB=0.5kg的A、B两物体,弹簧的劲度系数为100N/m.箱子放在水平地面上,平衡后剪断A、B间的连线,A将做简谐运动,求:(g=10m/s2)
(1)在剪断绳子后瞬间,A、B物体的加速度分别是多大?
(2)物体A的振幅?
(3)当A运动到最高点时,木箱对地面的压力大小?
16.如图所示,将弹簧振子从平衡位置O向右拉开4cm后放手,让它做简谐运动,已知从放手到第一次回到平衡位置的时间为0.1s,求:
(1)弹簧振子的振幅、周期、频率;
(2)振子在5s时间内通过的路程;
(3)振子从0.2s到0.3s向哪个方向做怎样的运动?
参考答案
1.C
【解析】
A.由图像可知,从t1到t2,振子从平衡位置向x轴正向运动,即振子正从O点向b点运动,选项A错误;
B.在t=0时刻,振子在平衡位置,即振子的位置在O点,选项B错误;
C.在t=t1时刻,振子振子在平衡位置,此时速度最大,选项C正确;
D.在t=t2时刻,振子的位移最大,回复力最大,加速度最大,选项D错误。
故选C。
2.D
【解析】
摆长为L的周期
摆长为的周期为
故小球完成一次全振动的时间为
故选D。
3.C
【解析】
A.根据可得
即在同一地点,单摆做简谐振动的周期的平方与其摆长成正比,选项A正确,不符合题意;
B.
弹簧振子做简谐振动时,振动系统的势能与动能之和保持不变,选项B正确,不符合题意;
C.
根据可知,在同一地点,当摆长不变时,单摆做简谐振动的周期不变,与摆球质量无关,选项C错误,符合题意;
D.
系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率,选项D正确,不符合题意。
故选C。
4.A
【解析】
AB.
图中O点是平衡位置,根据F=-kx,,可知,物块经过O点时位移最小,则其回复力、加速度最小,故A正确B错误;
C.
物块做简谐运动,物块同向经过关于平衡位置对称的两点时动量相等,所以如果在t2时刻物块的动量也为p,t2-t1的最小值小于等于,故C错误;
D.
物块经过同一位置或关于平衡位置对称的位置时动能相等,如果在t2时刻物块的动能也为Ek,则t2-t1的最小值可以小于T,故D错误。
故选A。
5.C
【解析】
A.
根据a=?,每次通过同一位置时,加速度相同,故A错误;
B.
经过同一位置,势能相同,由于机械能一定,故动能也相同,故B错误;
C.
经过同一位置,可能离开平衡位置,也可能向平衡位置运动,故速度有两个可能的方向,故C正确;
D.
因为位移是初位置指向末位置的有向线段,末位置都为平衡位置,故位移相同,D错误
6.C
【解析】
小球做简谐运动,O点为弹簧振子的平衡位置,系统机械能守恒,在O点弹性势能为零,动能最大;在小球从B点向O点运动的过程中,弹力不断减小,故合力减小,加速度减小,速度增大,即小球做加速度不断减小的加速运动;故选C。
点睛:本题考查了简谐运动的回复力、速度、加速度与位移的关系,要结合牛顿第二定律的对称性和能量守恒定律进行分析.
7.B
【解析】
A.由图可知,质点振动的振幅为,故A错误;
B.由图可知,质点振动的周期为,故B正确;
C.在时,质点在正的最大位移处,位移最大,故C错误;
D.在时,质点在平衡位置处,位移为零,速度最大,正沿轴的负方向运动,故D错误;
故选B。
8.B
【解析】
AB.b
摆垂直纸面向里拉开一微小角度后释放,使得其他4个单摆都做受迫振动,受迫振动的频率等于驱动力的频率,所以4个单摆频率相同,周期也一样,所以A错误B正确
CD.当驱动力的频率接近物体的固有频率时,振幅最大,即达到共振.根据知,d摆长与b摆长相等,则驱动力的周期等于d摆的固有周期,发生共振,所以d摆振幅最大,CD错误
9.BD
【解析】
A.由图像可知,质点振动的周期是T=4s,则频率是f=0.25Hz,振幅是2cm,选项A错误;
B.质点经过5s通过的路程总共是5A=10cm,选项B正确;
C.质点在t=2s和t=4s两时刻的位移大小相等,但方向相反,选项C错误;
D.因为
则质点做简谐运动的表达式为
选项D正确。
故选BD。
10.BD
【解析】
AB.摇把的转速为
它的周期
转动摇把时,弹簧振子做受迫振动;振子做受迫振动,振动周期等于驱动力的周期,当振子稳定振动时,它的振动周期是0.25s,频率为
A错误,B正确;
C.摇把转动的周期与弹簧振子固有周期相差越小,振子的振幅越大,并不是转速越大,弹簧振子的振幅就越大,故C错误;
D.当转速减小时,弹簧振子的受迫振动周期渐渐接近振子的固有周期,所以弹簧的振幅增大,故D正确。
故选BD。
11.0.8
-0.1
最大
增加
【解析】
[1]由,可得,则周期
。
[2]
由,初相位为。
[3]
时,位移
。
[4]
根据,振子是从正向最大位移处开始振动,当振子振动了半个周期,振子振动到了负向最大位移,所以加速度达到了最大值。
[5]从到振子是从最大位移向平衡位置振动,速度逐渐增大,振子的动能逐渐增大。
12.1.25
B点
0.16
【解析】
[1]由图乙所示图象可知,单摆周期T
=
0.8
s,单摆的频率
[2]由图乙所示图象可知,在t
=
0时,摆球处于负的最大位移,摆球向右运动方向为正方向,因此开始时,摆球在B处。
[3]由单摆周期公式得,这个摆的摆长为
13.(1);;(2)
【解析】
(1)记录纸匀速运动,振子振动的周期等于记录纸运动位移所用时间,因此由图可知
再根据图像可以看出振幅
(2)根据牛顿第二定律可得,在最高点时
代入数据解得加速度大小
14.(1)A=2cm,T=4s;(2)L=4m
【解析】
(1)由图可知振幅A=2cm;周期T=4s;
(2)由单摆的周期公式
得
带入数据解得摆长
L=4m
15.(1)5m/s2和10
m/s2;(2)5cm;(3)55N
【解析】
(1)平衡后剪断A、B间细线,A将做简谐振动,B做自由落体运动,即B的加速度为g=10
m/s2;
以A为研究对象,此时受向下的重力和弹簧的竖直向上的弹力,而弹簧的弹力为(mA+mB)g,据牛顿第二定律得
(2)剪短绳子瞬间有
kx1=(mA+mB)g
平衡位置时,弹簧的伸长量:有
kx2=mAg
故振幅为
A=x1﹣x2=0.05m=5cm
(3)剪断A、B间的连线,A将做简谐运动,且在最低点的恢复力为mBg;根据简谐运动的对称性,到达最高点时恢复力大小也为mBg;据此可知弹簧对A的弹力为5N,方向向上,所以弹簧对顶部的拉力也为f=5N;
再以木箱为研究对象,据平衡态可知
F=Mg+F=55N+5N=55N
由牛顿第三定律可知,木箱对地面的压力等于55N;
16.(1)4cm;0.4s;2.5Hz;(2)2m;(3)
向右做加速运动。
【解析】
(1)简谐运动中,振幅是振子离开平衡位置的最大距离,故振幅为
A=4cm;
从最大位移回到平衡位置的时间为,则
故周期为
T=0.4s,频率为
(2)周期为0.4s,故5s内完成12.5次全振动;一个全振动内通过的路程等于4倍振幅,故5s内路程为振幅的50倍,即
S=50A=200cm=2m
(3)
周期为0.4s,则振子从0.2s到0.3s从C点向O点运动,即向右做加速运动。
单元检测试题(解析版)
1.如图甲所示,水平的光滑杆上有一弹簧振子,振子以O点为平衡位置,在a、b两点之间做简谐运动,其振动图像如图乙所示。由振动图像可以得知( )
A.从t1到t2,振子正从O点向a点运动
B.在t=0时刻,振子的位置在a点
C.在t=t1时刻,振子的速度最大
D.在t=t2时刻,振子的加速度为零
2.如图所示,一单摆摆长为L,在悬点正下方0.19L处有一钉子。现将摆球向左拉开到A处,使摆角θ<5°,放手使其摆动,则此单摆的振动周期为( )
A.
B.
C.
D.
3.下列说法错误的是( )
A.在同一地点,单摆做简谐振动的周期的平方与其摆长成正比
B.弹簧振子做简谐振动时,振动系统的势能与动能之和保持不变
C.在同一地点,当摆长不变时,摆球质量越大,单摆做简谐振动的周期越小
D.系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率
4.如图所示,一根轻质弹簧上端固定在天花板,下端连接一个可视为质点的物块,不计空气阻力,物块沿竖直方向以O点为中心点,在C、D之间做周期为T的简谐运动。已知在初时刻t1时物块的动量为p、动能为Ek。下列说法正确的是( )
A.当物块通过O点时,其回复力最小
B.物块运动至C点时,其加速度最小
C.如果在末时刻t2时刻物块的动量也为p,则从t1到t2之间的时间间隔的最小值为T
D.如果在末时刻t2时刻物块的动能也为Ek,则从t1到t2之间的时间间隔的最小值为T
5.做简谐运动的物体,在不同时刻通过同一确定位置时可能不相同的物理量是(
)
A.加速度
B.动能
C.速度
D.位移
6.如图,O点为弹簧振子的平衡位置,小球在B、C间做无摩擦的往复运动。在小球从B运动到O的过程中,小球的(
)
A.速度不断增大,加速度不断增大
B.速度不断减小,加速度不断增大
C.速度不断增大,加速度不断减小
D.速度不断减小,加速度不断减小
7.某质点的振动图象如图所示,根据图象可知( )
A.质点振动的振幅为
B.质点振动的周期为
C.t=1s时,质点有负的最大位移
D.t=2s时,质点的运动速度为零
8.如图所示,在一根张紧的水平绳上挂有
5
个单摆,其中
b
摆球质量最大,其余
4
个摆球质量相等,摆长关系为
Lc>Lb=Ld>La>Le,现将
b
摆垂直纸面向里拉开一微小角度后释放,经过一段时间后,其余各摆均振动起来并达到稳定,下列叙述正确的是(
)
A.4
个单摆的周期
Tc>Td>Ta>Te
B.4
个单摆的频率
fa=fc=fd=fe
C.4
个单摆的振幅
Aa=Ac=Ad=Ae
D.4
个单摆中
c
摆的振幅最大
9.一质点做简谐运动,其位移x与时间t的关系图象如图所示,由图可知( )
A.质点振动的频率是4Hz,振幅是2cm
B.质点经过5s通过的路程总共是10cm
C.质点在t=2s和t=4s两时刻的位移相等
D.质点做简谐运动的表达式为
10.如图所示.曲轴上挂一个弹簧振子,转动摇把,曲轴可带动弹簧振子上、下振动.开始时不转动摇把,让振子自由振动,测得其频率为2Hz.现匀速转动摇把,转速为240r/min.则:(
)
A.当振子稳定振动时,它的振动周期是0.5s
B.当振子稳定振动时,它的振动频率是4Hz
C.当转速增大时,弹簧振子的振幅增大
D.当转速减小时,弹簧振子的振幅增大
11.一弹簧振子的位移x随时间t变化的关系式为x=0.1sin(2.5πt+),位移x的单位为m,时间t的单位为s。则弹簧振子的周期为_____s;弹簧振子的振动初相位_______;在t=0.4s时,振子的位移_____m,振子的加速度是_______(填最大或最小)。在t=0.4s到t=0.6s时间段内振子的动能________(填增加或减小)。
12.如图甲是一个单摆振动的情形,O是它的平衡位置,B、C是摆球所能到达的最远位置。设向右为正方向,图乙是这个单摆的振动图象。根据图象可得,单摆振动的频率是_______Hz;开始时摆球在______位置;若当地的重力加速度为10
m/s2,试求这个摆的摆长是______m。
13.一轻弹簧上端固定在支架顶端,下端悬挂一物块,物块上装有一只记录笔,在竖直面内放置有一记录纸。当物块上下振动时,以速率v水平向左拉动记录纸,记录笔在纸上留下印迹如图所示。y1、y2、x0、2x0为纸上印迹的位置坐标:
(1)求物块振动的周期和振幅;
(2)若弹簧的劲度系数为k,物块与笔的总质量为m,写出物块振动到最高点时的加速度大小。
14.如图所示是某一单摆做简谐运动的图象,已知当地重力加速度。
(1)该简谐运动的振幅A和周期T分别是多少?
(2)该单摆的摆长L是多少?
15.如图所示,在质量M=5kg的无下底的木箱顶部用一轻弹簧悬挂质量分别为mA=1kg、mB=0.5kg的A、B两物体,弹簧的劲度系数为100N/m.箱子放在水平地面上,平衡后剪断A、B间的连线,A将做简谐运动,求:(g=10m/s2)
(1)在剪断绳子后瞬间,A、B物体的加速度分别是多大?
(2)物体A的振幅?
(3)当A运动到最高点时,木箱对地面的压力大小?
16.如图所示,将弹簧振子从平衡位置O向右拉开4cm后放手,让它做简谐运动,已知从放手到第一次回到平衡位置的时间为0.1s,求:
(1)弹簧振子的振幅、周期、频率;
(2)振子在5s时间内通过的路程;
(3)振子从0.2s到0.3s向哪个方向做怎样的运动?
参考答案
1.C
【解析】
A.由图像可知,从t1到t2,振子从平衡位置向x轴正向运动,即振子正从O点向b点运动,选项A错误;
B.在t=0时刻,振子在平衡位置,即振子的位置在O点,选项B错误;
C.在t=t1时刻,振子振子在平衡位置,此时速度最大,选项C正确;
D.在t=t2时刻,振子的位移最大,回复力最大,加速度最大,选项D错误。
故选C。
2.D
【解析】
摆长为L的周期
摆长为的周期为
故小球完成一次全振动的时间为
故选D。
3.C
【解析】
A.根据可得
即在同一地点,单摆做简谐振动的周期的平方与其摆长成正比,选项A正确,不符合题意;
B.
弹簧振子做简谐振动时,振动系统的势能与动能之和保持不变,选项B正确,不符合题意;
C.
根据可知,在同一地点,当摆长不变时,单摆做简谐振动的周期不变,与摆球质量无关,选项C错误,符合题意;
D.
系统做稳定的受迫振动时,系统振动的频率等于周期性驱动力的频率,选项D正确,不符合题意。
故选C。
4.A
【解析】
AB.
图中O点是平衡位置,根据F=-kx,,可知,物块经过O点时位移最小,则其回复力、加速度最小,故A正确B错误;
C.
物块做简谐运动,物块同向经过关于平衡位置对称的两点时动量相等,所以如果在t2时刻物块的动量也为p,t2-t1的最小值小于等于,故C错误;
D.
物块经过同一位置或关于平衡位置对称的位置时动能相等,如果在t2时刻物块的动能也为Ek,则t2-t1的最小值可以小于T,故D错误。
故选A。
5.C
【解析】
A.
根据a=?,每次通过同一位置时,加速度相同,故A错误;
B.
经过同一位置,势能相同,由于机械能一定,故动能也相同,故B错误;
C.
经过同一位置,可能离开平衡位置,也可能向平衡位置运动,故速度有两个可能的方向,故C正确;
D.
因为位移是初位置指向末位置的有向线段,末位置都为平衡位置,故位移相同,D错误
6.C
【解析】
小球做简谐运动,O点为弹簧振子的平衡位置,系统机械能守恒,在O点弹性势能为零,动能最大;在小球从B点向O点运动的过程中,弹力不断减小,故合力减小,加速度减小,速度增大,即小球做加速度不断减小的加速运动;故选C。
点睛:本题考查了简谐运动的回复力、速度、加速度与位移的关系,要结合牛顿第二定律的对称性和能量守恒定律进行分析.
7.B
【解析】
A.由图可知,质点振动的振幅为,故A错误;
B.由图可知,质点振动的周期为,故B正确;
C.在时,质点在正的最大位移处,位移最大,故C错误;
D.在时,质点在平衡位置处,位移为零,速度最大,正沿轴的负方向运动,故D错误;
故选B。
8.B
【解析】
AB.b
摆垂直纸面向里拉开一微小角度后释放,使得其他4个单摆都做受迫振动,受迫振动的频率等于驱动力的频率,所以4个单摆频率相同,周期也一样,所以A错误B正确
CD.当驱动力的频率接近物体的固有频率时,振幅最大,即达到共振.根据知,d摆长与b摆长相等,则驱动力的周期等于d摆的固有周期,发生共振,所以d摆振幅最大,CD错误
9.BD
【解析】
A.由图像可知,质点振动的周期是T=4s,则频率是f=0.25Hz,振幅是2cm,选项A错误;
B.质点经过5s通过的路程总共是5A=10cm,选项B正确;
C.质点在t=2s和t=4s两时刻的位移大小相等,但方向相反,选项C错误;
D.因为
则质点做简谐运动的表达式为
选项D正确。
故选BD。
10.BD
【解析】
AB.摇把的转速为
它的周期
转动摇把时,弹簧振子做受迫振动;振子做受迫振动,振动周期等于驱动力的周期,当振子稳定振动时,它的振动周期是0.25s,频率为
A错误,B正确;
C.摇把转动的周期与弹簧振子固有周期相差越小,振子的振幅越大,并不是转速越大,弹簧振子的振幅就越大,故C错误;
D.当转速减小时,弹簧振子的受迫振动周期渐渐接近振子的固有周期,所以弹簧的振幅增大,故D正确。
故选BD。
11.0.8
-0.1
最大
增加
【解析】
[1]由,可得,则周期
。
[2]
由,初相位为。
[3]
时,位移
。
[4]
根据,振子是从正向最大位移处开始振动,当振子振动了半个周期,振子振动到了负向最大位移,所以加速度达到了最大值。
[5]从到振子是从最大位移向平衡位置振动,速度逐渐增大,振子的动能逐渐增大。
12.1.25
B点
0.16
【解析】
[1]由图乙所示图象可知,单摆周期T
=
0.8
s,单摆的频率
[2]由图乙所示图象可知,在t
=
0时,摆球处于负的最大位移,摆球向右运动方向为正方向,因此开始时,摆球在B处。
[3]由单摆周期公式得,这个摆的摆长为
13.(1);;(2)
【解析】
(1)记录纸匀速运动,振子振动的周期等于记录纸运动位移所用时间,因此由图可知
再根据图像可以看出振幅
(2)根据牛顿第二定律可得,在最高点时
代入数据解得加速度大小
14.(1)A=2cm,T=4s;(2)L=4m
【解析】
(1)由图可知振幅A=2cm;周期T=4s;
(2)由单摆的周期公式
得
带入数据解得摆长
L=4m
15.(1)5m/s2和10
m/s2;(2)5cm;(3)55N
【解析】
(1)平衡后剪断A、B间细线,A将做简谐振动,B做自由落体运动,即B的加速度为g=10
m/s2;
以A为研究对象,此时受向下的重力和弹簧的竖直向上的弹力,而弹簧的弹力为(mA+mB)g,据牛顿第二定律得
(2)剪短绳子瞬间有
kx1=(mA+mB)g
平衡位置时,弹簧的伸长量:有
kx2=mAg
故振幅为
A=x1﹣x2=0.05m=5cm
(3)剪断A、B间的连线,A将做简谐运动,且在最低点的恢复力为mBg;根据简谐运动的对称性,到达最高点时恢复力大小也为mBg;据此可知弹簧对A的弹力为5N,方向向上,所以弹簧对顶部的拉力也为f=5N;
再以木箱为研究对象,据平衡态可知
F=Mg+F=55N+5N=55N
由牛顿第三定律可知,木箱对地面的压力等于55N;
16.(1)4cm;0.4s;2.5Hz;(2)2m;(3)
向右做加速运动。
【解析】
(1)简谐运动中,振幅是振子离开平衡位置的最大距离,故振幅为
A=4cm;
从最大位移回到平衡位置的时间为,则
故周期为
T=0.4s,频率为
(2)周期为0.4s,故5s内完成12.5次全振动;一个全振动内通过的路程等于4倍振幅,故5s内路程为振幅的50倍,即
S=50A=200cm=2m
(3)
周期为0.4s,则振子从0.2s到0.3s从C点向O点运动,即向右做加速运动。
