北师大版八年级下册数学 6.2平行四边形的判定 同步检测(含答案)
文档属性
| 名称 | 北师大版八年级下册数学 6.2平行四边形的判定 同步检测(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 379.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-21 21:33:50 | ||
图片预览



文档简介
6.2平行四边形的判定
同步检测
一、选择题
1.下列给出的条件中,不能判断四边形ABCD是平行四边形的是( )
A.
AB∥CD,AD=BC
B.
∠A=∠C,∠B=∠D
C.
AB∥CD,AD∥BC
D.
AB=CD,AD=BC
2.如图,平行四边形中,,、分别在和的延长线上,AE∥BD,,,则的长是(
).
A.
B.
C.
D.
3.在四边形ABCD中,AD∥BC,分别添加下列条件:①AB∥CD;②AB=CD;③AD=BC;④∠B=∠D;⑤∠A=∠C,其中能使四边形ABCD成为平行四边形的条件有( )
A.
5个
B.
4个
C.
3个
D.
2个
4.具有下列条件的四边形中,是平行四边形的是()
A.
一组对角相等B.
两条对角线互相垂直
C.
两组对边分别相等
D.
两组邻角互补
5.已知四边形ABCD的四条边分别是a、b、c、d.其中a、c是对边,且a2+b2+c2+d2=2ac+2bd,则四边形一定是( )
A.
平行四边形B.
矩形
C.
菱形
D.
正方形
6.一个四边形的三个内角的度数依次如下选项,其中是平行四边形的是( )
A.
88°,108°,88°
B.
88°,104°,108°
C.
88°,92°,92°
D.
88°,92°,88°
7.已知在四边形ABCD中,AB//CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是(
)
A.
AD=BC
B.
AC=BD
C.
∠A=∠C
D.
∠A=∠B
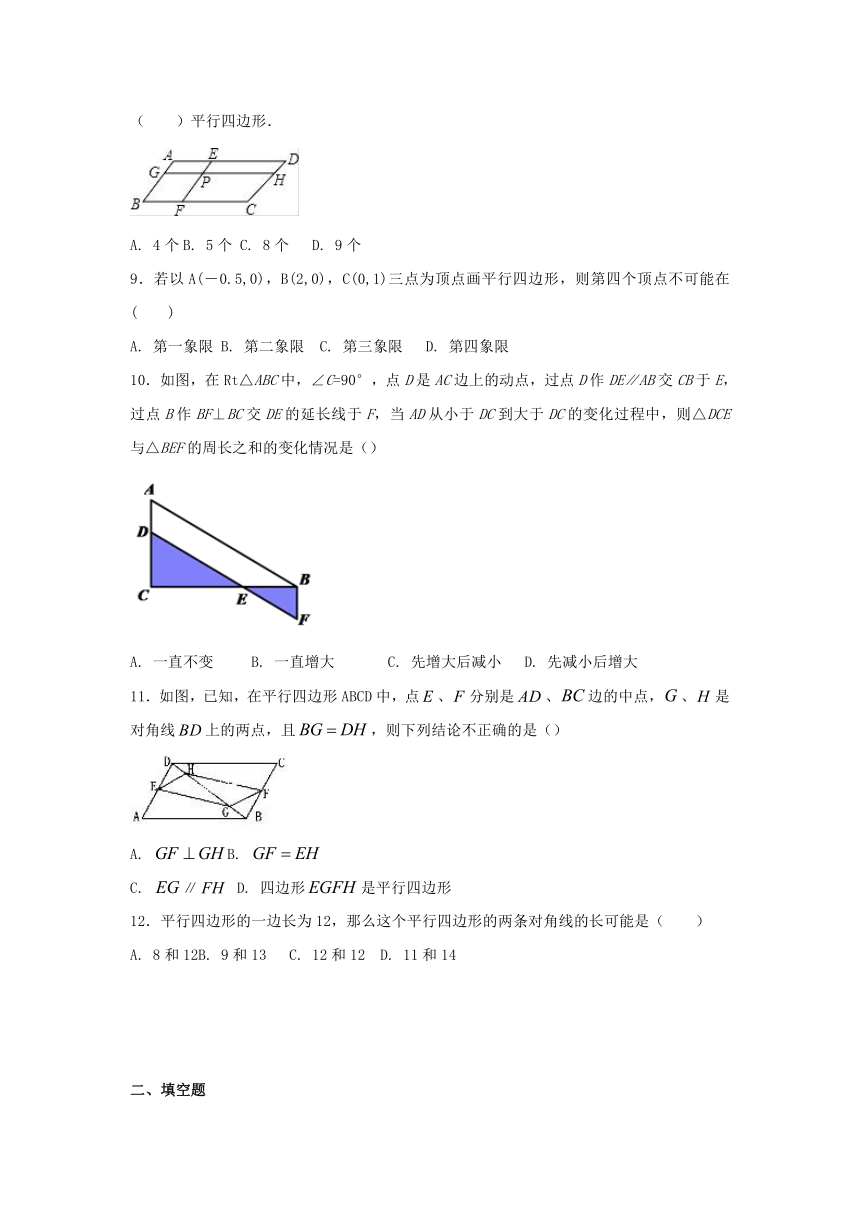
8.如图,在平行四边形ABCD中,过点P作直线EF、GH分别平行于AB、BC,那么图中共有( )平行四边形.
A.
4个B.
5个
C.
8个
D.
9个
9.若以A(-0.5,0),B(2,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在( )
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
10.如图,在Rt△ABC中,∠C=90°,点D是AC边上的动点,过点D作DE∥AB交CB于E,过点B作BF⊥BC交DE的延长线于F,当AD从小于DC到大于DC的变化过程中,则△DCE与△BEF的周长之和的变化情况是()
A.
一直不变
B.
一直增大
C.
先增大后减小
D.
先减小后增大
11.如图,已知,在平行四边形ABCD中,点、分别是、边的中点,、是对角线上的两点,且,则下列结论不正确的是()
A.
B.
C.
∥
D.
四边形是平行四边形
12.平行四边形的一边长为12,那么这个平行四边形的两条对角线的长可能是( )
A.
8和12B.
9和13
C.
12和12
D.
11和14
二、填空题
13.如图,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有______种.
14.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为_________.
15.要做一个平行四边形框架,只要将两根木条AC、BD的中点重叠并用钉子固定,这样四边形ABCD就是平行四边形,这种做法的依据是
_______________________.
16.如图所示,在△ABC中,AB=AC=7cm,D是BC上的一点,且DE∥AC,DF∥AB,则DE+DF=___.
17.如图,在□中,⊥于点,⊥于点.若,,且□的周长为40,则□的面积为_______。
三、解答题
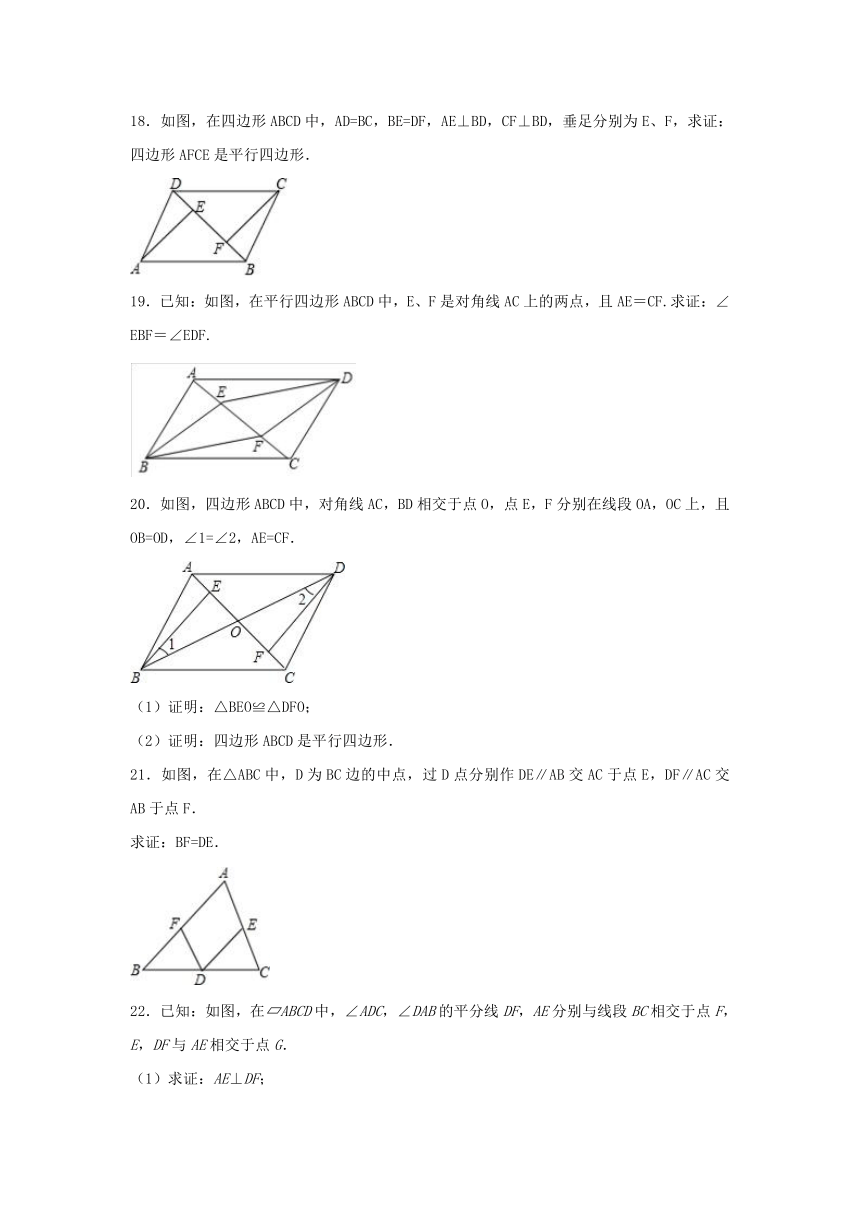
18.如图,在四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:四边形AFCE是平行四边形.
19.已知:如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF.求证:∠EBF=∠EDF.
20.如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.
(1)证明:△BEO≌△DFO;
(2)证明:四边形ABCD是平行四边形.
21.如图,在△ABC中,D为BC边的中点,过D点分别作DE∥AB交AC于点E,DF∥AC交AB于点F.
求证:BF=DE.
22.已知:如图,在?ABCD中,∠ADC,∠DAB的平分线DF,AE分别与线段BC相交于点F,E,DF与AE相交于点G.
(1)求证:AE⊥DF;
(2)若AD=10,AB=6,AE=4,求DF的长.
23.如图,在平行四边形ABCD中,∠ABC=120°,∠BAD的平分线交BC于点E,交DC的延长线于点F,过点F作FG∥CE,且FG=CE,连结DG,EG,BG,CG.
(1)试判断四边形EGFC的形状;
(2)求证:△DCG≌△BEG;
(3)试求出∠BDG的度数.
参考答案
1.A
2.B
3.B
4.C
5.A
6.D
7.C
8.D
9.C
10.A
11.A
12.D
13.4
14.24
15.两条对角线分别平分的四边形是平行四边形
16.7cm
17.48
18.证明:连接AF、CE,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,AE∥CF,
∵BE=DF,
∴DE=BF,
在Rt△ADE后Rt△CBF中,
,
∴Rt△ADE≌Rt△CBF,
∴AE=CF,∵AE∥CF,
∴四边形AECF是平行四边形.
19.解析:证明:连结BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC.
∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴∠EBF=∠EDF.
20.解析:(1)证明:∵∠EOB与∠FOD是对顶角,
∴∠EOB=∠FOD,
在△BEO和△DFO中
,
∴△BEO≌△DFO(ASA)
(2)证明:由(1)可知△BEO≌△DFO,
∴OE=OF,
∵AE=CF,
∴OA=OC,
∵OB=OD,
∴四边形ABCD为平行四边形.
21.解析:
∵DE∥AB,DF∥AC,
∴DE∥AF,DF∥AE,
∴四边形AFDE是平行四边形,
∴DE=AF,
∵D为BC边的中点,
∴BD=DC,∵DF∥AC,
∴BF=AF,
∴BF=DE.
22.(1)证明见解析;(2).
解析:(1)∵在?ABCD中,AB∥CD,
∴∠ADC+∠DAB=180°,
∵DF,AE分别是∠ADC,∠DAB的平分线,
∴∠ADF=∠CDF=∠ADC,∠DAE=∠BAE=∠DAB,
∴∠ADF+∠DAE=(∠ADC+∠DAB)=90°,
∴∠AGD=90°,即AE⊥DF;
(2)如图,过点D作DH∥AE,交BC的延长线于点H,则四边形AEHD是平行四边形,且FD⊥DH,
∴DH=AE=4,EH=AD=10,
∵在?ABCD中,AD∥BC,∴∠ADF=∠CFD,∠DAE=∠BEA,
∴∠CDF=∠CFD,∠BAE=∠BEA,
∴DC=FC,AB=EB,
在?ABCD中,AD=BC=10,AB=DC=6,∴CF=BE=6,BF=BC-CF=10-6=4,
∴FE=BE-BF=6-4=2,∴FH=FE+EH=12,
在Rt△FDH中,DF=
.
23.
且四边形是平行四边形.
四边形是平行四边形,
平分
得出
四边形是平行四边形.
判定是等边三角形,
又
由判定
是等边三角形,
试题解析:
且
∴四边形是平行四边形.
∵四边形是平行四边形,
平分
又
四边形是平行四边形.
是等边三角形,
又
是等边三角形,
同步检测
一、选择题
1.下列给出的条件中,不能判断四边形ABCD是平行四边形的是( )
A.
AB∥CD,AD=BC
B.
∠A=∠C,∠B=∠D
C.
AB∥CD,AD∥BC
D.
AB=CD,AD=BC
2.如图,平行四边形中,,、分别在和的延长线上,AE∥BD,,,则的长是(
).
A.
B.
C.
D.
3.在四边形ABCD中,AD∥BC,分别添加下列条件:①AB∥CD;②AB=CD;③AD=BC;④∠B=∠D;⑤∠A=∠C,其中能使四边形ABCD成为平行四边形的条件有( )
A.
5个
B.
4个
C.
3个
D.
2个
4.具有下列条件的四边形中,是平行四边形的是()
A.
一组对角相等B.
两条对角线互相垂直
C.
两组对边分别相等
D.
两组邻角互补
5.已知四边形ABCD的四条边分别是a、b、c、d.其中a、c是对边,且a2+b2+c2+d2=2ac+2bd,则四边形一定是( )
A.
平行四边形B.
矩形
C.
菱形
D.
正方形
6.一个四边形的三个内角的度数依次如下选项,其中是平行四边形的是( )
A.
88°,108°,88°
B.
88°,104°,108°
C.
88°,92°,92°
D.
88°,92°,88°
7.已知在四边形ABCD中,AB//CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是(
)
A.
AD=BC
B.
AC=BD
C.
∠A=∠C
D.
∠A=∠B
8.如图,在平行四边形ABCD中,过点P作直线EF、GH分别平行于AB、BC,那么图中共有( )平行四边形.
A.
4个B.
5个
C.
8个
D.
9个
9.若以A(-0.5,0),B(2,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在( )
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
10.如图,在Rt△ABC中,∠C=90°,点D是AC边上的动点,过点D作DE∥AB交CB于E,过点B作BF⊥BC交DE的延长线于F,当AD从小于DC到大于DC的变化过程中,则△DCE与△BEF的周长之和的变化情况是()
A.
一直不变
B.
一直增大
C.
先增大后减小
D.
先减小后增大
11.如图,已知,在平行四边形ABCD中,点、分别是、边的中点,、是对角线上的两点,且,则下列结论不正确的是()
A.
B.
C.
∥
D.
四边形是平行四边形
12.平行四边形的一边长为12,那么这个平行四边形的两条对角线的长可能是( )
A.
8和12B.
9和13
C.
12和12
D.
11和14
二、填空题
13.如图,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有______种.
14.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为_________.
15.要做一个平行四边形框架,只要将两根木条AC、BD的中点重叠并用钉子固定,这样四边形ABCD就是平行四边形,这种做法的依据是
_______________________.
16.如图所示,在△ABC中,AB=AC=7cm,D是BC上的一点,且DE∥AC,DF∥AB,则DE+DF=___.
17.如图,在□中,⊥于点,⊥于点.若,,且□的周长为40,则□的面积为_______。
三、解答题
18.如图,在四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:四边形AFCE是平行四边形.
19.已知:如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF.求证:∠EBF=∠EDF.
20.如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.
(1)证明:△BEO≌△DFO;
(2)证明:四边形ABCD是平行四边形.
21.如图,在△ABC中,D为BC边的中点,过D点分别作DE∥AB交AC于点E,DF∥AC交AB于点F.
求证:BF=DE.
22.已知:如图,在?ABCD中,∠ADC,∠DAB的平分线DF,AE分别与线段BC相交于点F,E,DF与AE相交于点G.
(1)求证:AE⊥DF;
(2)若AD=10,AB=6,AE=4,求DF的长.
23.如图,在平行四边形ABCD中,∠ABC=120°,∠BAD的平分线交BC于点E,交DC的延长线于点F,过点F作FG∥CE,且FG=CE,连结DG,EG,BG,CG.
(1)试判断四边形EGFC的形状;
(2)求证:△DCG≌△BEG;
(3)试求出∠BDG的度数.
参考答案
1.A
2.B
3.B
4.C
5.A
6.D
7.C
8.D
9.C
10.A
11.A
12.D
13.4
14.24
15.两条对角线分别平分的四边形是平行四边形
16.7cm
17.48
18.证明:连接AF、CE,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,AE∥CF,
∵BE=DF,
∴DE=BF,
在Rt△ADE后Rt△CBF中,
,
∴Rt△ADE≌Rt△CBF,
∴AE=CF,∵AE∥CF,
∴四边形AECF是平行四边形.
19.解析:证明:连结BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC.
∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴∠EBF=∠EDF.
20.解析:(1)证明:∵∠EOB与∠FOD是对顶角,
∴∠EOB=∠FOD,
在△BEO和△DFO中
,
∴△BEO≌△DFO(ASA)
(2)证明:由(1)可知△BEO≌△DFO,
∴OE=OF,
∵AE=CF,
∴OA=OC,
∵OB=OD,
∴四边形ABCD为平行四边形.
21.解析:
∵DE∥AB,DF∥AC,
∴DE∥AF,DF∥AE,
∴四边形AFDE是平行四边形,
∴DE=AF,
∵D为BC边的中点,
∴BD=DC,∵DF∥AC,
∴BF=AF,
∴BF=DE.
22.(1)证明见解析;(2).
解析:(1)∵在?ABCD中,AB∥CD,
∴∠ADC+∠DAB=180°,
∵DF,AE分别是∠ADC,∠DAB的平分线,
∴∠ADF=∠CDF=∠ADC,∠DAE=∠BAE=∠DAB,
∴∠ADF+∠DAE=(∠ADC+∠DAB)=90°,
∴∠AGD=90°,即AE⊥DF;
(2)如图,过点D作DH∥AE,交BC的延长线于点H,则四边形AEHD是平行四边形,且FD⊥DH,
∴DH=AE=4,EH=AD=10,
∵在?ABCD中,AD∥BC,∴∠ADF=∠CFD,∠DAE=∠BEA,
∴∠CDF=∠CFD,∠BAE=∠BEA,
∴DC=FC,AB=EB,
在?ABCD中,AD=BC=10,AB=DC=6,∴CF=BE=6,BF=BC-CF=10-6=4,
∴FE=BE-BF=6-4=2,∴FH=FE+EH=12,
在Rt△FDH中,DF=
.
23.
且四边形是平行四边形.
四边形是平行四边形,
平分
得出
四边形是平行四边形.
判定是等边三角形,
又
由判定
是等边三角形,
试题解析:
且
∴四边形是平行四边形.
∵四边形是平行四边形,
平分
又
四边形是平行四边形.
是等边三角形,
又
是等边三角形,
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
