2019-2020学年沪教版六年级下册期末考试数学试卷(二)(解析版)
文档属性
| 名称 | 2019-2020学年沪教版六年级下册期末考试数学试卷(二)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 292.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-22 12:57:13 | ||
图片预览




文档简介
2019-2020学年沪教版六年级下册期末考试数学试卷(二)
一.选择题(共10小题)
1.下列结论正确的有( )个:
①规定了原点,正方向和单位长度的直线叫数轴
②最小的整数是0
③正数,负数和零统称有理数
④数轴上的点都表示有理数.
A.0
B.1
C.2
D.3
2.在数轴上,原点左边的点表示的数是( )
A.+8
B.﹣8
C.+8和﹣8
D.无法确定
3.已知m<n,那么下列各式中,不一定成立的是( )
A.2m<2n
B.3﹣m>3﹣n
C.mc2<nc2
D.m﹣3<n﹣1
4.下列式子中,( )是方程.
A.30﹣0.4x=6
B.x﹣56>200
C.4y+5b
D.78+96=164
5.把一个角的两边分别延伸到原来的3倍,这个角的度数也扩大到原来的3倍.( )
A.正确
B.错误
C.无法确定
6.把一个平角分成两个角,其中一个角是钝角,另一个角是( )
A.锐角
B.直角
C.钝角
D.周角
7.下面各组数中,结果不一定相同的是( )
A.2×2和22
B.x2和x×2
C.82和8×8
D.ab×1和ab
8.下面的图形中,( )组图形的周长一样.
A.
B.
C.
9.已知:a<0,b>0.且|a|>|b|.则|b+1|﹣|a﹣b|等于( )
A.2a﹣b+1
B.1+a
C.a﹣1
D.﹣1﹣a
10.已知:关于x,y的方程组和有相同的解,那么a,b的值分别为( )
A.a=b=
B.a=b=
C.a=b=
D.a=b=
二.填空题(共8小题)
11.如图甲的周长与乙的周长比较,甲的周长
乙的周长.(填大于、等于或小于).
12.解方程x=,x=
.
13.计算﹣24=
.
14.图中甲的周长
乙的周长(填“大于“小于”或“等于“).
15.如果x+4=7,那么3x+12=
.
16.写出直线上点A,B,C,D,E表示的数.
A
;B
;C
;D
;E
.
17.一个分数,如果分子加上8,化简后等于;如果分母加上5,化简后等于,那么原来的分数是
.
18.在式子<<中,要使两端的不等式成立,那么要填入的整数x是
.
三.判断题(共5小题)
19.数轴上左边的数比右边的数小.(0在中间,既不在左边也不在右边).
(判断对错)
20.方程(3x﹣15)÷12=1的解是x=1.
(判断对错)
21.将一张圆形纸对折三次,得到的角是120°.
(判断对错)
22.m2与2m相同.
(判断对错)
23.甲、乙两只蚂蚁分别沿着边长为2cm正方形和直径为2cm的圆走一圈,它们的速度一样,甲先爬行完一圈.
(判断对错)
四.计算题(共5小题)
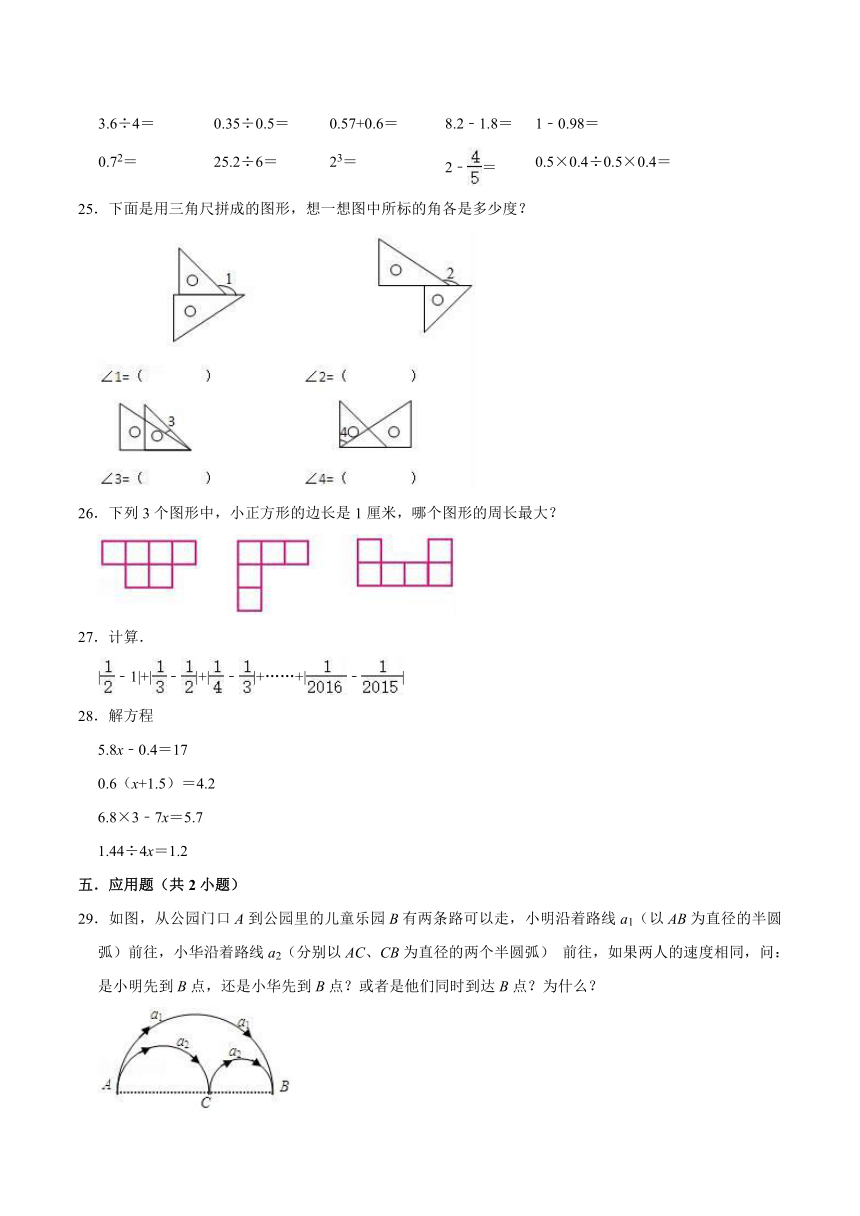
24.直接写出下面各题的得数.
3.6÷4=
0.35÷0.5=
0.57+0.6=
8.2﹣1.8=
1﹣0.98=
0.72=
25.2÷6=
23=
2﹣=
0.5×0.4÷0.5×0.4=
25.下面是用三角尺拼成的图形,想一想图中所标的角各是多少度?
26.下列3个图形中,小正方形的边长是1厘米,哪个图形的周长最大?
27.计算.
|﹣1|+|﹣|+|﹣|+……+|﹣|
28.解方程
5.8x﹣0.4=17
0.6(x+1.5)=4.2
6.8×3﹣7x=5.7
1.44÷4x=1.2
五.应用题(共2小题)
29.如图,从公园门口A到公园里的儿童乐园B有两条路可以走,小明沿着路线a1(以AB为直径的半圆弧)前往,小华沿着路线a2(分别以AC、CB为直径的两个半圆弧)
前往,如果两人的速度相同,问:是小明先到B点,还是小华先到B点?或者是他们同时到达B点?为什么?
30.小李和小张买了同样数量的信纸和同样数量的信封.小李用自己买的信纸和信封写了一些信,每封信都用1张信纸;小张也用自己买的信纸写了一些信,但每封信都用了3张信纸;结果小李用掉了所有信封但余下50张信纸,而小张用掉了所有的信纸且余下了50个信封.那么他们每人买了多少个信封和多少张信纸?
参考答案与试题解析
一.选择题(共10小题)
1.【分析】利用下面的基本知识解答即可:
①数轴的定义是规定了原点,正方向和单位长度的直线叫数轴.
②在有理数范围内没有最小的整数.
③整数,分数统称有理数.
④数轴上的点不仅表示有理数还表示无理数.
【解答】解:①数轴的定义是规定了原点,正方向和单位长度的直线叫数轴.
②在有理数范围没有最小的整数.
③整数,分数统称有理数.
④数轴上的点不仅表示有理数还表示无理数.
所以①只有1个答案的说法是正确的.
故选:B.
【点评】本题考查了数轴的定义及有理数的概念,及数轴上的点表示哪些数,考查了学生的判断能力.
2.【分析】根据数轴上点表示的数,原点左边的数表示负数,右边的数表示正数,据此解答即可.
【解答】解:在数轴上,原点左边的点所表示的是数是负数,只有﹣8是负数.
故选:B.
【点评】此题考查了数轴,熟练掌握数轴上点表示的数是解本题的关键.
3.【分析】由于m、n的取值范围不确定,故可考虑利用特例来说明,若能直接利用不等式性质的就用不等式性质进行判断即可.
【解答】解:A、如果m<n,根据不等式两边同时乘以2,不等号的方向不改变,则2m<2n,所以A成立.
B、如果m<n,且m、n为负数,根据不等式两边同时被3减,不等号的方向要改变,则有3﹣m>3﹣n;且m、n为非负数,根据不等式两边同时被3减,不等号的方向要改变,则3﹣m>3﹣n,所以B对.
C、如果m<n,c2≥0,当c为非0的数时,不等式两边同时乘以c2,不等号方向不变,所以mc2<nc2成立;当c为0时mc2=nc2,所以C不一定成立.
D、如果m<n,根据不等式两边左边去掉3,不等号方向不变,则m﹣3<n﹣1.所以D对.
故选:C.
【点评】主要考查了不等式的基本性质.不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
4.【分析】方程必须满足两个条件(缺一不可):1、含有未知数;2、是等式.据此解答即可.
【解答】解:A、30﹣0.4x=6,有未知数,也是等式,所以是方程;
B、x﹣56>200,不是等式,所以不是方程;
C、4y+5b,不是等式,所以不是方程;
D、78+96=164,没有未知数,所以不是方程;
只有A是方程.
故选:A.
【点评】此题考查了方程需要满足的条件,即含有未知数且是等式.
5.【分析】根据角的含义:由一点引出的两条射线所组成的图形叫做角;可知角的大小只与角的两边叉开的大小有关,和两边的长短无关,一个角的两边无论怎么延长,角的大小不变.
【解答】解:由分析可知,角的大小与两边的长短无关,所以一个角的两边的长度扩大到原来的3倍,这个角的度数大小不变;
所以本题“这个角的度数也扩大到原来的3倍”说法错误;
故选:B.
【点评】此题考查了角的含义,应明确:角的大小只与角的两边叉开的大小有关和两边的长短无关.
6.【分析】平角等于180度,其中钝角大于90度,小于180度,用“180﹣钝角”所得的角的度数小于90度,根据锐角的含义:锐角是大于0°,小于90°的角;进而得出结论.
【解答】解:平角是180度,其中钝角大于90度,小于180度,用“180﹣钝角”所得的角的度数小于90度,所以另一个角一定是锐角.
故选:A.
【点评】此题考查了锐角、平角和钝角的含义,应注意知识的灵活运用.
7.【分析】根据乘方的意义和乘法的计算法则解答即可.
【解答】解:A、2×2=4,22=4,结果相等,
B、x2和x×2,当x=0或2时,结果相等,否则结果不相同;
C、82=64,8×8=64,结果相等,
D、ab×1=ab;结果相等,
故选:B.
【点评】本题关键是理解乘方的意义和乘法的计算法则.
8.【分析】根据图形周长的定义和长方形的周长公式,利用线段的平移的方法,判断出哪组图形的周长一样即可.
【解答】解:A:,两个图形的周长相等;
B:,右边的图形比左边的图形多了画斜线的两条边的长度,两个图形的周长不相等;
C:,右边的图形比左边的图形多了画斜线的两条边的长度,两个图形的周长不相等.
故选:A.
【点评】此题主要考查了长度大小的比较,要熟练掌握,注意线段的平移的应用.
9.【分析】先根据a<0,b>0,且|a|>|b|,判断出b+1及a﹣b的符号,再去绝对值符号,合并同类项即可.
【解答】解:因为a<0,b>0,且|a|>|b|,
所以b+1>0,a﹣b<0,
|b+1|﹣|a﹣b|
=b+1﹣(b﹣a)
=b+1﹣b+a
=a+1.
故选:B.
【点评】本题考查的是整式的加减,熟知绝对值的性质是解答此题的关键.
10.【分析】因为方程组有相同的解,所以只需求出一组解代入另一组,即可求出未知数的值.
【解答】解:因为关于x、y的方程组
和的解相同,
所以这个解既满足2x﹣y=2,又满足x+y=4,
应该是方程组
的解.
解这个方程组得:
又因为
既满足2ax﹣by=1,又满足ax+2by=2,
应该是方程组
的解,
所以
解得:
故选:A.
【点评】本题考查了同解方程组的知识,解答此题的关键是熟知方程组有公共解的含义,考查了学生对题意的理解能力.
二.填空题(共8小题)
11.【分析】根据题意知甲的周长是长方形的一条长和宽,和中间折线的和,图形乙的周长是长方形的一条长和宽,和中间折线的和.它们的周长相等.据此解答.
【解答】解:由分析可知,甲、乙的周长都是长方形的一条长和宽,和中间折线的和.
所以甲的周长等于乙的周长.
故答案为:等于.
【点评】本题主要考查了学生对平面图形周长意义的掌握情况.
12.【分析】根据等式的性质,方程两边同时除以即可得解.
【解答】解:
x=
x÷=÷
x=
故答案为:.
【点评】在解方程时应根据等式的性质,即等式两边同加上、同减去或同除以、同乘上某一个数(0除外),等式的两边仍相等,同时注意等号上下要对齐.
13.【分析】根据有理数乘方的法则进行计算即可.
【解答】解:﹣24=﹣16,
故答案为:﹣16.
【点评】本题考查的是有理数乘方的法则,解答此题时要注意﹣24与(﹣2)4的区别.
14.【分析】因为甲的周长=长方形的一组邻边的和+中间的曲线的长,乙的周长=长方形的另一组邻边的和+中间的曲线的长,根据长方形的特征:对边相等;进行解答继而得出结论.
【解答】解:甲的周长=长方形的一组邻边的和+中间的曲线的长,
乙的周长=长方形的另一组邻边的和+中间的曲线的长,
因为长方形对边相等,所以甲的周长等于乙的周长;
答:甲的周长等于乙的周长.
故答案为:等于.
【点评】解答此题应根据长方形的特征,并结合周长的计算方法进行解答.
15.【分析】首先把3x+12化成3(x+4),然后把x+4=7代入3(x+4),求出算式的值是多少即可.
【解答】解:因为x+4=7,
所以3x+12
=3(x+4)
=3×7
=21
故答案为:21.
【点评】此题主要考查了方程的解和解方程,要熟练掌握,解答此题的关键是把所求的算式灵活变形.
16.【分析】在数轴上,原正左边的为负数,右边的为正数,原点用0表示,A在原点左边3个单位长度,表示﹣3,B在原点左边2个单位长度,表示﹣2,C在原点左边,1到2之间分成3等份,点C表示的数占2等份,又在1的左边,因此点C表示的数是1+,所以表示的数是﹣;同理点D表示的数是﹣;点E在原点右边两个长度单位加上,表示2;据此解决.
【解答】解:
【点评】本题的解题关键是知道数轴上以0为原点,0的右边表示正数,左边表示负数.
17.【分析】可设分子为x,分母为y,则,解方程组求解即可.
【解答】解:设原来的分数分子为x,分母为y,则
则
故原分数为.
故答案为:.
【点评】本题考查了分数的基本性质,本题关键是列出方程组,题目难度较大.
18.【分析】把式子<<,看作“<,”与“<,”分别求出两个不等式中的x的取值范围,进而确定x的值.
【解答】解:因为<<,
所以<,
24x<31×733
x<,
x<946.79,
又因为<,
31x>733×40,
所以x>,
x>945.8,
所以945.8<x<946.79,
因为x为整数,
所以x=946,
故答案为:946.
【点评】解答此题的关键是将给出的式子看作两个不等式,解不等式求出x的取值范围,进而求出x的值.
三.判断题(共5小题)
19.【分析】数轴上,0的右边是正数,0的左边是负数,负数都小于正数,也就是0左边的数都比0右边的数小,由此求解.
【解答】解:
数轴上左边的数比右边的数小,如:﹣4<﹣3<0<2.
原题说法正确.
故答案为:√.
【点评】本题是考查数轴的认识.数轴是规定了原点(0点)、方向和单位长度的一条直线,数轴上左边的数比右边的数小.
20.【分析】首先根据等式的性质,两边同时乘12,然后两边再同时加上15,最后两边同时除以3即可判断.
【解答】解:(3x﹣15)÷12=1
(3x﹣15)÷12×12=1×12
3x﹣15=12
3x﹣15+15=12+15
3x=27
3x÷3=27÷3
x=9
所以方程(3x﹣15)÷12=1的解是x=9,
所以题中说法不正确.
故答案为:×.
【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等.
21.【分析】把这张圆形纸片对折1次,折成的角是以这张圆形纸片的圆心为顶点,两条半径为边的平角,平角=180°,再对折1次,就是把平角平均分成2分,每份是90°,再对折1次,就是把90°的角再平均分成2份,每份是45°.据此判断即可.
【解答】解:将一张圆形的纸对折,再对折,再对折,得到的角是45度.
所以题干说法错误.
故答案为:×.
【点评】本题是考查简单图形的折叠问题.可以操作一下.
22.【分析】m2表示两个m相乘,而2m表示两个m相加,因为它们的意义不同,所以计算结果也就不一定相等.
【解答】解:m2表示两个m相乘,而2m表示两个m相加,所以m2与2m相同的说法是错误的.
故答案为:×.
【点评】明确两个算式意义的不同是解决此题的关键.
23.【分析】根据正方形的周长公式C=4a和圆的周长公式C=πd,分别求出正方形和圆的周长,再比较即可得出答案.
【解答】解:2×4=8(厘米)
3.14×2=6.28(厘米)
8>6.28
所以乙先爬完一圈,原题说法错误.
故答案为:×.
【点评】本题是利用圆和正方形的周长公式解决问题.
四.计算题(共5小题)
24.【分析】根据小数加减乘除法的计算方法以及分数减法的计算方法求解;
0.72=0.7×0.7;23=2×2×2,由此求解.
【解答】解:
3.6÷4=0.9
0.35÷0.5=0.7
0.57+0.6=1.17
8.2﹣1.8=6.4
1﹣0.98=0.02
0.72=0.49
25.2÷6=4.2
23=8
2﹣=1
0.5×0.4÷0.5×0.4=0.16
【点评】本题属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性.
25.【分析】(1)用平角减去45°的角;
(2)用平角减去30°的角;
(3)用45°减去30°的角;
(4)用90°减去30°的角.
【解答】解:(1)∠1=180°﹣45°=135°
(2)∠2=180°﹣30°=150°
(3)∠3=45°﹣30°=15°
(4)∠5=90°﹣30°=60°
故答案为:.
【点评】考查了角的计算,关键是熟悉三角板上角的度数.
26.【分析】小正方形的边长是1厘米,数出各个图形的周长是由几个小正方形的边长组成的,然后比较即可判断周长的大小即可.
【解答】解:
1×12=12(厘米)
1×12=12(厘米)
1×14=14(厘米)
12=12<14,
答:最右边的图形周长最大.
【点评】本题关键是理解周长的意义,根据数一数的方法进行求解即可.
27.【分析】先根据绝对值为大数减小数,去掉绝对值符号,再计算加减即可.
【解答】解:|﹣1|+|﹣|+|﹣|+……+|﹣|
=1﹣++……+
=1﹣
=.
【点评】本题考查了绝对值的计算,关键是掌握去绝对值符号应等于大数减小数.
28.【分析】(1)首先根据等式的性质,两边同时加上0.4,然后两边再同时除以5.8即可.
(2)首先根据等式的性质,两边同时除以0.6,然后两边再同时减去1.5即可.
(3)首先根据等式的性质,两边同时加上7x,然后两边再同时减去5.7,最后两边同时除以7即可.
(4)首先根据等式的性质,两边同时乘4x,然后两边再同时除以4.8即可.
【解答】解:(1)5.8x﹣0.4=17
5.8x﹣0.4+0.4=17+0.4
5.8x=17.4
5.8x÷5.8=17.4÷5.8
x=3
(2)0.6(x+1.5)=4.2
0.6(x+1.5)÷0.6=4.2÷0.6
x+1.5=7
x+1.5﹣1.5=7﹣1.5
x=5.5
(3)6.8×3﹣7x=5.7
20.4﹣7x=5.7
20.4﹣7x+7x=5.7+7x
5.7+7x=20.4
5.7+7x﹣5.7=20.4﹣5.7
7x=14.7
7x÷7=14.7÷7
x=2.1
(4)1.44÷4x=1.2
1.44÷4x×4x=1.2×4x
4.8x=1.44
4.8x÷4.8=1.44÷4.8
x=0.3
【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等.
五.应用题(共2小题)
29.【分析】分别设出大圆和小圆的直径,利用圆的周长公式C=πd分别求出半圆弧长,即可分别求得两个路径的长,然后进行比较即可.
【解答】解:设AC为d1,BC=d2,则大圆的直径为d1+d2,
路线a2的长度为:πd1÷2+πd2÷2=π(d1+d2)÷2,
路线a1的长度为:π(d1+d2)÷2;
所以路线a1、路线a2两条路的长度一样长;
由于两人的速度相同,所以他们同时到达B点.
答:他们同时到达B点,因为路线a1、路线a2两条路的长度一样长.
【点评】本题主要是灵活利用圆的周长公式解决问题.
30.【分析】设他们每人买了x个信封和y张信纸,则小李用掉的信纸是x张,就有y﹣x=50,则小王就用掉了个信封,就有x﹣=50,由此列出方程组,求出其解即可.
【解答】解:设他们每人买了x个信封和y张信纸,根据题意得:
①+②×3得:
2x=200
2x÷2=200÷2
x=100
把x=100代入①得:
y﹣100=50
y﹣100+100=50+100
y=150
答:他们每人买了100个信封和150张信纸.
【点评】本题主要考查了二元一次方程组在解决实际问题中的应用,解答时找出数量之间的关系是解答的关键.
一.选择题(共10小题)
1.下列结论正确的有( )个:
①规定了原点,正方向和单位长度的直线叫数轴
②最小的整数是0
③正数,负数和零统称有理数
④数轴上的点都表示有理数.
A.0
B.1
C.2
D.3
2.在数轴上,原点左边的点表示的数是( )
A.+8
B.﹣8
C.+8和﹣8
D.无法确定
3.已知m<n,那么下列各式中,不一定成立的是( )
A.2m<2n
B.3﹣m>3﹣n
C.mc2<nc2
D.m﹣3<n﹣1
4.下列式子中,( )是方程.
A.30﹣0.4x=6
B.x﹣56>200
C.4y+5b
D.78+96=164
5.把一个角的两边分别延伸到原来的3倍,这个角的度数也扩大到原来的3倍.( )
A.正确
B.错误
C.无法确定
6.把一个平角分成两个角,其中一个角是钝角,另一个角是( )
A.锐角
B.直角
C.钝角
D.周角
7.下面各组数中,结果不一定相同的是( )
A.2×2和22
B.x2和x×2
C.82和8×8
D.ab×1和ab
8.下面的图形中,( )组图形的周长一样.
A.
B.
C.
9.已知:a<0,b>0.且|a|>|b|.则|b+1|﹣|a﹣b|等于( )
A.2a﹣b+1
B.1+a
C.a﹣1
D.﹣1﹣a
10.已知:关于x,y的方程组和有相同的解,那么a,b的值分别为( )
A.a=b=
B.a=b=
C.a=b=
D.a=b=
二.填空题(共8小题)
11.如图甲的周长与乙的周长比较,甲的周长
乙的周长.(填大于、等于或小于).
12.解方程x=,x=
.
13.计算﹣24=
.
14.图中甲的周长
乙的周长(填“大于“小于”或“等于“).
15.如果x+4=7,那么3x+12=
.
16.写出直线上点A,B,C,D,E表示的数.
A
;B
;C
;D
;E
.
17.一个分数,如果分子加上8,化简后等于;如果分母加上5,化简后等于,那么原来的分数是
.
18.在式子<<中,要使两端的不等式成立,那么要填入的整数x是
.
三.判断题(共5小题)
19.数轴上左边的数比右边的数小.(0在中间,既不在左边也不在右边).
(判断对错)
20.方程(3x﹣15)÷12=1的解是x=1.
(判断对错)
21.将一张圆形纸对折三次,得到的角是120°.
(判断对错)
22.m2与2m相同.
(判断对错)
23.甲、乙两只蚂蚁分别沿着边长为2cm正方形和直径为2cm的圆走一圈,它们的速度一样,甲先爬行完一圈.
(判断对错)
四.计算题(共5小题)
24.直接写出下面各题的得数.
3.6÷4=
0.35÷0.5=
0.57+0.6=
8.2﹣1.8=
1﹣0.98=
0.72=
25.2÷6=
23=
2﹣=
0.5×0.4÷0.5×0.4=
25.下面是用三角尺拼成的图形,想一想图中所标的角各是多少度?
26.下列3个图形中,小正方形的边长是1厘米,哪个图形的周长最大?
27.计算.
|﹣1|+|﹣|+|﹣|+……+|﹣|
28.解方程
5.8x﹣0.4=17
0.6(x+1.5)=4.2
6.8×3﹣7x=5.7
1.44÷4x=1.2
五.应用题(共2小题)
29.如图,从公园门口A到公园里的儿童乐园B有两条路可以走,小明沿着路线a1(以AB为直径的半圆弧)前往,小华沿着路线a2(分别以AC、CB为直径的两个半圆弧)
前往,如果两人的速度相同,问:是小明先到B点,还是小华先到B点?或者是他们同时到达B点?为什么?
30.小李和小张买了同样数量的信纸和同样数量的信封.小李用自己买的信纸和信封写了一些信,每封信都用1张信纸;小张也用自己买的信纸写了一些信,但每封信都用了3张信纸;结果小李用掉了所有信封但余下50张信纸,而小张用掉了所有的信纸且余下了50个信封.那么他们每人买了多少个信封和多少张信纸?
参考答案与试题解析
一.选择题(共10小题)
1.【分析】利用下面的基本知识解答即可:
①数轴的定义是规定了原点,正方向和单位长度的直线叫数轴.
②在有理数范围内没有最小的整数.
③整数,分数统称有理数.
④数轴上的点不仅表示有理数还表示无理数.
【解答】解:①数轴的定义是规定了原点,正方向和单位长度的直线叫数轴.
②在有理数范围没有最小的整数.
③整数,分数统称有理数.
④数轴上的点不仅表示有理数还表示无理数.
所以①只有1个答案的说法是正确的.
故选:B.
【点评】本题考查了数轴的定义及有理数的概念,及数轴上的点表示哪些数,考查了学生的判断能力.
2.【分析】根据数轴上点表示的数,原点左边的数表示负数,右边的数表示正数,据此解答即可.
【解答】解:在数轴上,原点左边的点所表示的是数是负数,只有﹣8是负数.
故选:B.
【点评】此题考查了数轴,熟练掌握数轴上点表示的数是解本题的关键.
3.【分析】由于m、n的取值范围不确定,故可考虑利用特例来说明,若能直接利用不等式性质的就用不等式性质进行判断即可.
【解答】解:A、如果m<n,根据不等式两边同时乘以2,不等号的方向不改变,则2m<2n,所以A成立.
B、如果m<n,且m、n为负数,根据不等式两边同时被3减,不等号的方向要改变,则有3﹣m>3﹣n;且m、n为非负数,根据不等式两边同时被3减,不等号的方向要改变,则3﹣m>3﹣n,所以B对.
C、如果m<n,c2≥0,当c为非0的数时,不等式两边同时乘以c2,不等号方向不变,所以mc2<nc2成立;当c为0时mc2=nc2,所以C不一定成立.
D、如果m<n,根据不等式两边左边去掉3,不等号方向不变,则m﹣3<n﹣1.所以D对.
故选:C.
【点评】主要考查了不等式的基本性质.不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
4.【分析】方程必须满足两个条件(缺一不可):1、含有未知数;2、是等式.据此解答即可.
【解答】解:A、30﹣0.4x=6,有未知数,也是等式,所以是方程;
B、x﹣56>200,不是等式,所以不是方程;
C、4y+5b,不是等式,所以不是方程;
D、78+96=164,没有未知数,所以不是方程;
只有A是方程.
故选:A.
【点评】此题考查了方程需要满足的条件,即含有未知数且是等式.
5.【分析】根据角的含义:由一点引出的两条射线所组成的图形叫做角;可知角的大小只与角的两边叉开的大小有关,和两边的长短无关,一个角的两边无论怎么延长,角的大小不变.
【解答】解:由分析可知,角的大小与两边的长短无关,所以一个角的两边的长度扩大到原来的3倍,这个角的度数大小不变;
所以本题“这个角的度数也扩大到原来的3倍”说法错误;
故选:B.
【点评】此题考查了角的含义,应明确:角的大小只与角的两边叉开的大小有关和两边的长短无关.
6.【分析】平角等于180度,其中钝角大于90度,小于180度,用“180﹣钝角”所得的角的度数小于90度,根据锐角的含义:锐角是大于0°,小于90°的角;进而得出结论.
【解答】解:平角是180度,其中钝角大于90度,小于180度,用“180﹣钝角”所得的角的度数小于90度,所以另一个角一定是锐角.
故选:A.
【点评】此题考查了锐角、平角和钝角的含义,应注意知识的灵活运用.
7.【分析】根据乘方的意义和乘法的计算法则解答即可.
【解答】解:A、2×2=4,22=4,结果相等,
B、x2和x×2,当x=0或2时,结果相等,否则结果不相同;
C、82=64,8×8=64,结果相等,
D、ab×1=ab;结果相等,
故选:B.
【点评】本题关键是理解乘方的意义和乘法的计算法则.
8.【分析】根据图形周长的定义和长方形的周长公式,利用线段的平移的方法,判断出哪组图形的周长一样即可.
【解答】解:A:,两个图形的周长相等;
B:,右边的图形比左边的图形多了画斜线的两条边的长度,两个图形的周长不相等;
C:,右边的图形比左边的图形多了画斜线的两条边的长度,两个图形的周长不相等.
故选:A.
【点评】此题主要考查了长度大小的比较,要熟练掌握,注意线段的平移的应用.
9.【分析】先根据a<0,b>0,且|a|>|b|,判断出b+1及a﹣b的符号,再去绝对值符号,合并同类项即可.
【解答】解:因为a<0,b>0,且|a|>|b|,
所以b+1>0,a﹣b<0,
|b+1|﹣|a﹣b|
=b+1﹣(b﹣a)
=b+1﹣b+a
=a+1.
故选:B.
【点评】本题考查的是整式的加减,熟知绝对值的性质是解答此题的关键.
10.【分析】因为方程组有相同的解,所以只需求出一组解代入另一组,即可求出未知数的值.
【解答】解:因为关于x、y的方程组
和的解相同,
所以这个解既满足2x﹣y=2,又满足x+y=4,
应该是方程组
的解.
解这个方程组得:
又因为
既满足2ax﹣by=1,又满足ax+2by=2,
应该是方程组
的解,
所以
解得:
故选:A.
【点评】本题考查了同解方程组的知识,解答此题的关键是熟知方程组有公共解的含义,考查了学生对题意的理解能力.
二.填空题(共8小题)
11.【分析】根据题意知甲的周长是长方形的一条长和宽,和中间折线的和,图形乙的周长是长方形的一条长和宽,和中间折线的和.它们的周长相等.据此解答.
【解答】解:由分析可知,甲、乙的周长都是长方形的一条长和宽,和中间折线的和.
所以甲的周长等于乙的周长.
故答案为:等于.
【点评】本题主要考查了学生对平面图形周长意义的掌握情况.
12.【分析】根据等式的性质,方程两边同时除以即可得解.
【解答】解:
x=
x÷=÷
x=
故答案为:.
【点评】在解方程时应根据等式的性质,即等式两边同加上、同减去或同除以、同乘上某一个数(0除外),等式的两边仍相等,同时注意等号上下要对齐.
13.【分析】根据有理数乘方的法则进行计算即可.
【解答】解:﹣24=﹣16,
故答案为:﹣16.
【点评】本题考查的是有理数乘方的法则,解答此题时要注意﹣24与(﹣2)4的区别.
14.【分析】因为甲的周长=长方形的一组邻边的和+中间的曲线的长,乙的周长=长方形的另一组邻边的和+中间的曲线的长,根据长方形的特征:对边相等;进行解答继而得出结论.
【解答】解:甲的周长=长方形的一组邻边的和+中间的曲线的长,
乙的周长=长方形的另一组邻边的和+中间的曲线的长,
因为长方形对边相等,所以甲的周长等于乙的周长;
答:甲的周长等于乙的周长.
故答案为:等于.
【点评】解答此题应根据长方形的特征,并结合周长的计算方法进行解答.
15.【分析】首先把3x+12化成3(x+4),然后把x+4=7代入3(x+4),求出算式的值是多少即可.
【解答】解:因为x+4=7,
所以3x+12
=3(x+4)
=3×7
=21
故答案为:21.
【点评】此题主要考查了方程的解和解方程,要熟练掌握,解答此题的关键是把所求的算式灵活变形.
16.【分析】在数轴上,原正左边的为负数,右边的为正数,原点用0表示,A在原点左边3个单位长度,表示﹣3,B在原点左边2个单位长度,表示﹣2,C在原点左边,1到2之间分成3等份,点C表示的数占2等份,又在1的左边,因此点C表示的数是1+,所以表示的数是﹣;同理点D表示的数是﹣;点E在原点右边两个长度单位加上,表示2;据此解决.
【解答】解:
【点评】本题的解题关键是知道数轴上以0为原点,0的右边表示正数,左边表示负数.
17.【分析】可设分子为x,分母为y,则,解方程组求解即可.
【解答】解:设原来的分数分子为x,分母为y,则
则
故原分数为.
故答案为:.
【点评】本题考查了分数的基本性质,本题关键是列出方程组,题目难度较大.
18.【分析】把式子<<,看作“<,”与“<,”分别求出两个不等式中的x的取值范围,进而确定x的值.
【解答】解:因为<<,
所以<,
24x<31×733
x<,
x<946.79,
又因为<,
31x>733×40,
所以x>,
x>945.8,
所以945.8<x<946.79,
因为x为整数,
所以x=946,
故答案为:946.
【点评】解答此题的关键是将给出的式子看作两个不等式,解不等式求出x的取值范围,进而求出x的值.
三.判断题(共5小题)
19.【分析】数轴上,0的右边是正数,0的左边是负数,负数都小于正数,也就是0左边的数都比0右边的数小,由此求解.
【解答】解:
数轴上左边的数比右边的数小,如:﹣4<﹣3<0<2.
原题说法正确.
故答案为:√.
【点评】本题是考查数轴的认识.数轴是规定了原点(0点)、方向和单位长度的一条直线,数轴上左边的数比右边的数小.
20.【分析】首先根据等式的性质,两边同时乘12,然后两边再同时加上15,最后两边同时除以3即可判断.
【解答】解:(3x﹣15)÷12=1
(3x﹣15)÷12×12=1×12
3x﹣15=12
3x﹣15+15=12+15
3x=27
3x÷3=27÷3
x=9
所以方程(3x﹣15)÷12=1的解是x=9,
所以题中说法不正确.
故答案为:×.
【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等.
21.【分析】把这张圆形纸片对折1次,折成的角是以这张圆形纸片的圆心为顶点,两条半径为边的平角,平角=180°,再对折1次,就是把平角平均分成2分,每份是90°,再对折1次,就是把90°的角再平均分成2份,每份是45°.据此判断即可.
【解答】解:将一张圆形的纸对折,再对折,再对折,得到的角是45度.
所以题干说法错误.
故答案为:×.
【点评】本题是考查简单图形的折叠问题.可以操作一下.
22.【分析】m2表示两个m相乘,而2m表示两个m相加,因为它们的意义不同,所以计算结果也就不一定相等.
【解答】解:m2表示两个m相乘,而2m表示两个m相加,所以m2与2m相同的说法是错误的.
故答案为:×.
【点评】明确两个算式意义的不同是解决此题的关键.
23.【分析】根据正方形的周长公式C=4a和圆的周长公式C=πd,分别求出正方形和圆的周长,再比较即可得出答案.
【解答】解:2×4=8(厘米)
3.14×2=6.28(厘米)
8>6.28
所以乙先爬完一圈,原题说法错误.
故答案为:×.
【点评】本题是利用圆和正方形的周长公式解决问题.
四.计算题(共5小题)
24.【分析】根据小数加减乘除法的计算方法以及分数减法的计算方法求解;
0.72=0.7×0.7;23=2×2×2,由此求解.
【解答】解:
3.6÷4=0.9
0.35÷0.5=0.7
0.57+0.6=1.17
8.2﹣1.8=6.4
1﹣0.98=0.02
0.72=0.49
25.2÷6=4.2
23=8
2﹣=1
0.5×0.4÷0.5×0.4=0.16
【点评】本题属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性.
25.【分析】(1)用平角减去45°的角;
(2)用平角减去30°的角;
(3)用45°减去30°的角;
(4)用90°减去30°的角.
【解答】解:(1)∠1=180°﹣45°=135°
(2)∠2=180°﹣30°=150°
(3)∠3=45°﹣30°=15°
(4)∠5=90°﹣30°=60°
故答案为:.
【点评】考查了角的计算,关键是熟悉三角板上角的度数.
26.【分析】小正方形的边长是1厘米,数出各个图形的周长是由几个小正方形的边长组成的,然后比较即可判断周长的大小即可.
【解答】解:
1×12=12(厘米)
1×12=12(厘米)
1×14=14(厘米)
12=12<14,
答:最右边的图形周长最大.
【点评】本题关键是理解周长的意义,根据数一数的方法进行求解即可.
27.【分析】先根据绝对值为大数减小数,去掉绝对值符号,再计算加减即可.
【解答】解:|﹣1|+|﹣|+|﹣|+……+|﹣|
=1﹣++……+
=1﹣
=.
【点评】本题考查了绝对值的计算,关键是掌握去绝对值符号应等于大数减小数.
28.【分析】(1)首先根据等式的性质,两边同时加上0.4,然后两边再同时除以5.8即可.
(2)首先根据等式的性质,两边同时除以0.6,然后两边再同时减去1.5即可.
(3)首先根据等式的性质,两边同时加上7x,然后两边再同时减去5.7,最后两边同时除以7即可.
(4)首先根据等式的性质,两边同时乘4x,然后两边再同时除以4.8即可.
【解答】解:(1)5.8x﹣0.4=17
5.8x﹣0.4+0.4=17+0.4
5.8x=17.4
5.8x÷5.8=17.4÷5.8
x=3
(2)0.6(x+1.5)=4.2
0.6(x+1.5)÷0.6=4.2÷0.6
x+1.5=7
x+1.5﹣1.5=7﹣1.5
x=5.5
(3)6.8×3﹣7x=5.7
20.4﹣7x=5.7
20.4﹣7x+7x=5.7+7x
5.7+7x=20.4
5.7+7x﹣5.7=20.4﹣5.7
7x=14.7
7x÷7=14.7÷7
x=2.1
(4)1.44÷4x=1.2
1.44÷4x×4x=1.2×4x
4.8x=1.44
4.8x÷4.8=1.44÷4.8
x=0.3
【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等.
五.应用题(共2小题)
29.【分析】分别设出大圆和小圆的直径,利用圆的周长公式C=πd分别求出半圆弧长,即可分别求得两个路径的长,然后进行比较即可.
【解答】解:设AC为d1,BC=d2,则大圆的直径为d1+d2,
路线a2的长度为:πd1÷2+πd2÷2=π(d1+d2)÷2,
路线a1的长度为:π(d1+d2)÷2;
所以路线a1、路线a2两条路的长度一样长;
由于两人的速度相同,所以他们同时到达B点.
答:他们同时到达B点,因为路线a1、路线a2两条路的长度一样长.
【点评】本题主要是灵活利用圆的周长公式解决问题.
30.【分析】设他们每人买了x个信封和y张信纸,则小李用掉的信纸是x张,就有y﹣x=50,则小王就用掉了个信封,就有x﹣=50,由此列出方程组,求出其解即可.
【解答】解:设他们每人买了x个信封和y张信纸,根据题意得:
①+②×3得:
2x=200
2x÷2=200÷2
x=100
把x=100代入①得:
y﹣100=50
y﹣100+100=50+100
y=150
答:他们每人买了100个信封和150张信纸.
【点评】本题主要考查了二元一次方程组在解决实际问题中的应用,解答时找出数量之间的关系是解答的关键.
同课章节目录
