人教版九年级数学下册 28.1 余弦和正切课件 (第2课时 共19张PPT)
文档属性
| 名称 | 人教版九年级数学下册 28.1 余弦和正切课件 (第2课时 共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 974.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 09:15:49 | ||
图片预览




文档简介
(共19张PPT)
28
28.1
锐角三角函数
第2课时
余弦和正切
锐角三角函数
学习目标
1.通过类比正弦函数,了解锐角三角函数中余弦函数、正切函数的定义.
2.会求解简单的锐角三角函数.
导入新课
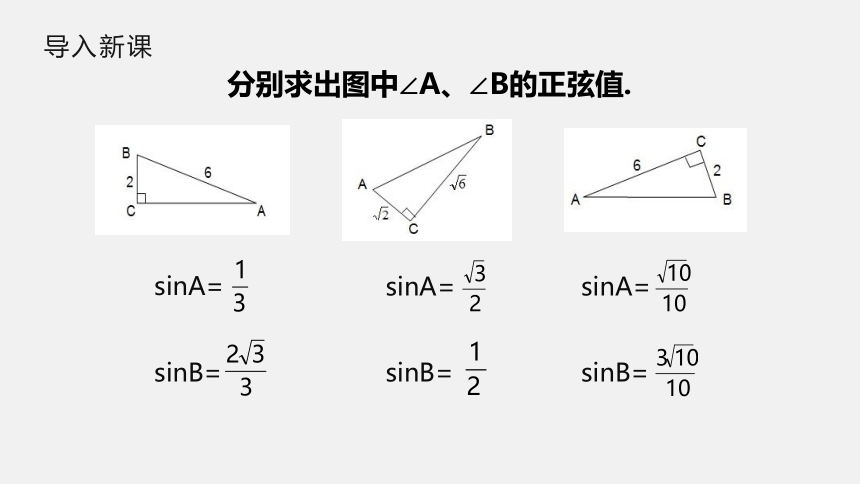
分别求出图中∠A、∠B的正弦值.
sinA=
sinB=
sinA=
sinB=
sinA=
sinB=
探究新知
知识点一
余弦、正切的定义
探究新知
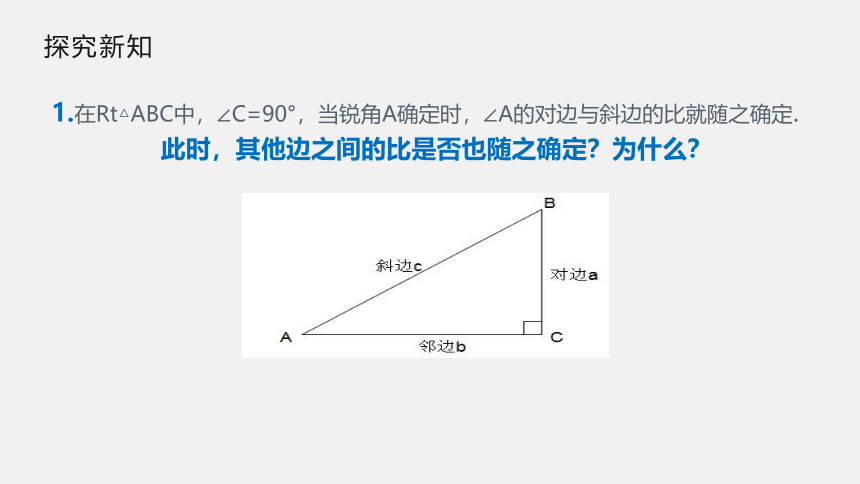
1.在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定.
此时,其他边之间的比是否也随之确定?为什么?
探究新知
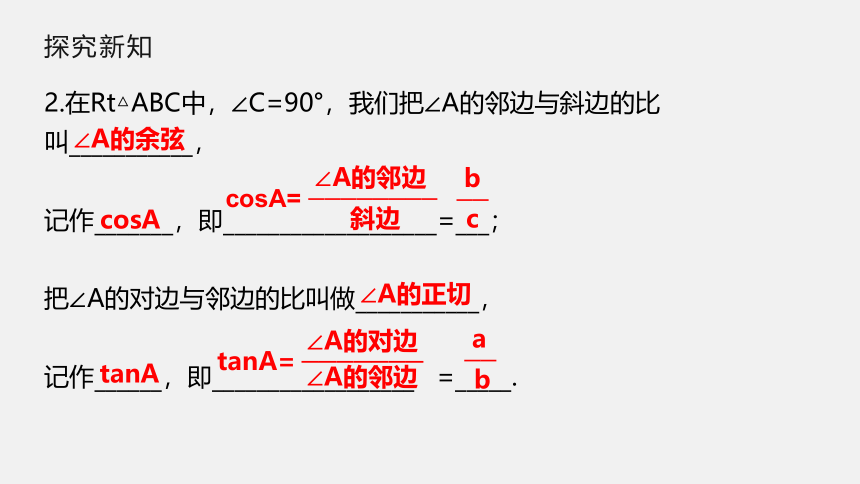
2.在Rt△ABC中,∠C=90°,我们把∠A的邻边与斜边的比
叫___________,
记作_______,即___________________=___;
把∠A的对边与邻边的比叫做___________,
记作______,即__________________
=_____.
∠A的余弦
cosA
cosA=
∠A的邻边
————————
斜边
b
——
c
∠A的正切
tanA
tanA=
∠A的对边
———————
∠A的邻边
a
——
b
探究新知
3.对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,
所以sinA是A的函数.同样地,_______,_______也是A的函数.
cosA
tanA
4.锐角A的_______、_______、_______都叫做∠A的锐角三角函数.
正弦
余弦
正切
应用新知
知识点一
余弦、正切的定义
应用新知
如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,
求sinA,cosA,tanA的值.
教材例2
解:
应用新知
练一练
1.在Rt△ABC中,∠C为直角,a=1,b=2,
则cosA=
tanA=
.
2.在Rt△ABC中,各边都扩大4倍,则锐角A的各三角函数值(
)
A.没有变化
B.分别扩大4倍
C.分别缩小到原来的
D.不能确定
A
应用新知
知识点二
余弦、正切的运用
应用新知
如图,在Rt△ABC中,∠C=90°,BC=6,sinA=
,求cosA、tanB的值.
解:
∵
sinA=
又AC=____________=____________=8,
∴
∴
应用新知
练一练
1.Rt△ABC中,∠C为直角,AC=5,BC=12,那么下列∠A的四个三角函数中正确的是(
)
A.
sinA=
B.sinA
=
C.tanA=
D.cosA=
B
应用新知
2.如图,P是∠α的边OA上一点,且P点的坐标为(3,4),
则cosα、tanα的值.
cosα=
tanα=
课堂小结
1.在Rt△ABC中,∠C=90°,我们把∠A的邻边与斜边的比叫____________,
记作_______,___________________=_____;
把∠A的对边与邻边的比叫做___________,
记作________,即_________________________=______.
∠A的余弦
cosA
cosA=
∠A的邻边
———————
斜边
∠A的正切
tanA
tanA=
∠A的对边
—————
∠A的邻边
课堂小结
2.对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,
所以sinA是A的函数.同样地,________,________也是A的函数.
cosA
tanA
3.锐角A的_______、_______、_______都叫做∠A的锐角三角函数.
正弦
余弦
正切
4.学习反思
强化训练
A.
B.
C.
D.
1.Rt△ABC中,∠C=90°,
如果AB=2,BC=1,
那么cosB的值为(
)
A
A.
B.
C.
D.
2.在Rt?ABC中,∠C=90°,
如果cos
A=
那么tanB的值为(
)
D
强化训练
3.在?ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C
的对边,则有(
)
C
A.b=
a?tanA
B.
b=
c?sinA
C.a=
c?cosB
D.
c=
a?sinA
4.已知在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,如果b=5a,那么∠A的正切值为
.
强化训练
5.如图,PA是圆O切线,
A为切点,PO交圆O于点B,
PA=8,OB=6,
求tan∠APO的值.
解:
∵
PA是圆O的切线
∴
PA⊥OA
∴
?POA是直角三角形
又∵
OA=OB
∴
28
28.1
锐角三角函数
第2课时
余弦和正切
锐角三角函数
学习目标
1.通过类比正弦函数,了解锐角三角函数中余弦函数、正切函数的定义.
2.会求解简单的锐角三角函数.
导入新课
分别求出图中∠A、∠B的正弦值.
sinA=
sinB=
sinA=
sinB=
sinA=
sinB=
探究新知
知识点一
余弦、正切的定义
探究新知
1.在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定.
此时,其他边之间的比是否也随之确定?为什么?
探究新知
2.在Rt△ABC中,∠C=90°,我们把∠A的邻边与斜边的比
叫___________,
记作_______,即___________________=___;
把∠A的对边与邻边的比叫做___________,
记作______,即__________________
=_____.
∠A的余弦
cosA
cosA=
∠A的邻边
————————
斜边
b
——
c
∠A的正切
tanA
tanA=
∠A的对边
———————
∠A的邻边
a
——
b
探究新知
3.对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,
所以sinA是A的函数.同样地,_______,_______也是A的函数.
cosA
tanA
4.锐角A的_______、_______、_______都叫做∠A的锐角三角函数.
正弦
余弦
正切
应用新知
知识点一
余弦、正切的定义
应用新知
如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,
求sinA,cosA,tanA的值.
教材例2
解:
应用新知
练一练
1.在Rt△ABC中,∠C为直角,a=1,b=2,
则cosA=
tanA=
.
2.在Rt△ABC中,各边都扩大4倍,则锐角A的各三角函数值(
)
A.没有变化
B.分别扩大4倍
C.分别缩小到原来的
D.不能确定
A
应用新知
知识点二
余弦、正切的运用
应用新知
如图,在Rt△ABC中,∠C=90°,BC=6,sinA=
,求cosA、tanB的值.
解:
∵
sinA=
又AC=____________=____________=8,
∴
∴
应用新知
练一练
1.Rt△ABC中,∠C为直角,AC=5,BC=12,那么下列∠A的四个三角函数中正确的是(
)
A.
sinA=
B.sinA
=
C.tanA=
D.cosA=
B
应用新知
2.如图,P是∠α的边OA上一点,且P点的坐标为(3,4),
则cosα、tanα的值.
cosα=
tanα=
课堂小结
1.在Rt△ABC中,∠C=90°,我们把∠A的邻边与斜边的比叫____________,
记作_______,___________________=_____;
把∠A的对边与邻边的比叫做___________,
记作________,即_________________________=______.
∠A的余弦
cosA
cosA=
∠A的邻边
———————
斜边
∠A的正切
tanA
tanA=
∠A的对边
—————
∠A的邻边
课堂小结
2.对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,
所以sinA是A的函数.同样地,________,________也是A的函数.
cosA
tanA
3.锐角A的_______、_______、_______都叫做∠A的锐角三角函数.
正弦
余弦
正切
4.学习反思
强化训练
A.
B.
C.
D.
1.Rt△ABC中,∠C=90°,
如果AB=2,BC=1,
那么cosB的值为(
)
A
A.
B.
C.
D.
2.在Rt?ABC中,∠C=90°,
如果cos
A=
那么tanB的值为(
)
D
强化训练
3.在?ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C
的对边,则有(
)
C
A.b=
a?tanA
B.
b=
c?sinA
C.a=
c?cosB
D.
c=
a?sinA
4.已知在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,如果b=5a,那么∠A的正切值为
.
强化训练
5.如图,PA是圆O切线,
A为切点,PO交圆O于点B,
PA=8,OB=6,
求tan∠APO的值.
解:
∵
PA是圆O的切线
∴
PA⊥OA
∴
?POA是直角三角形
又∵
OA=OB
∴
