人教版九年级数学下册 28.1 特殊的三角函数值 课件(第3课时 共19张PPT)
文档属性
| 名称 | 人教版九年级数学下册 28.1 特殊的三角函数值 课件(第3课时 共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 09:10:43 | ||
图片预览





文档简介
(共19张PPT)
28
28.1
锐角三角函数
第3课时
特殊的三角函数值
锐角三角函数
学习目标
1.理解特殊角的三角函数值的由来.
2.熟记30°,45°,60°的三角函数;
3.根据一个特殊角的三角函数值说出这个角.
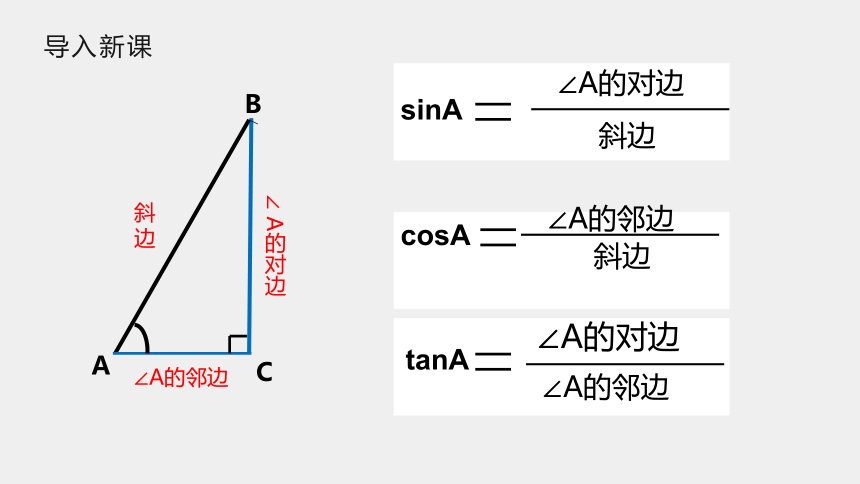
导入新课
A
B
C
∠
A的对边
∠A的邻边
斜边
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
斜边
∠A的对边
sinA
斜边
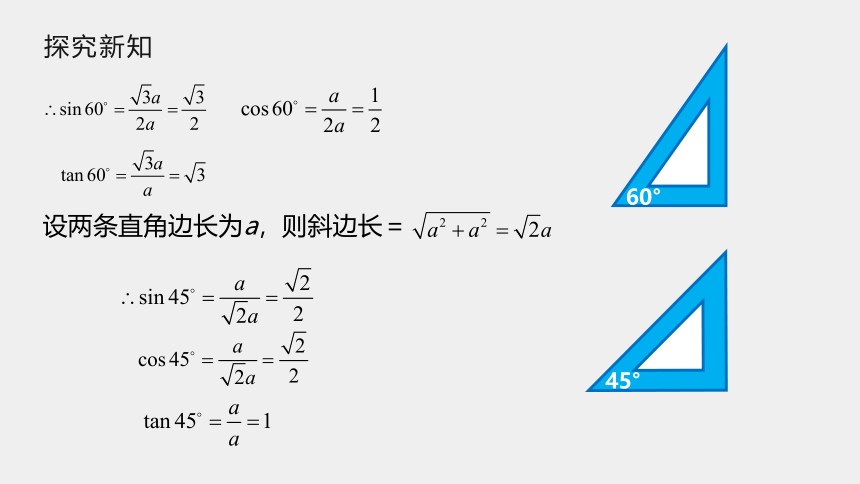
探究新知
活动
1
两块三角尺中有几个不同的锐角?
这几个锐角的正弦值、
余弦值和正切值各是多少?
30°
60°
45°
45°
探究新知
解:
设30°所对的直角边长为a,那么斜边长为2a.
另一条直角边长=
30°
探究新知
60°
45°
设两条直角边长为a,则斜边长=
探究新知
知识点一
特殊角三角函数
探究新知
30°
45°
60°
sinα
cosα
tanα
仔细观察,说说你发现这张表有哪些规律.
探究新知
求下列各式的值:
教材例3
(1)cos260°+sin260°
解:
cos260°+sin260°
=1
解:
=0
(2)
应用新知
练一练
1.在Rt△ABC中,∠C为直角,sinA=
,则cosB的值是(
)
A.
B.
C.1
D.
D
2.在Rt△ABC中,
2sin(α+20°)=
,则锐角α的度数是(
)
A.60°
B.80°
C.40°
D.以上结论都不对
C
应用新知
知识点二
利用特殊角三角函数
进行简单计算
应用新知
例4
A
B
C
解:
在图中,
∵
∠A=______
45°
求∠A的度数.
如图,在Rt△ABC中,∠C=90°,AB=
,BC=
α=
_____
应用新知
(2)如图,AO
是圆锥的高,OB
是底面半径,AO=
OB,
求α的度数.
60°
解:
在图中,
∵
∴
当A,B,为锐角时,若A≠B,
则sinA=sinB,cosA≠cosB,tanA=tanB.
应用新知
练一练—
计算
(1)2
cos45°
解:
(2)1-2sin30°cos30°.
解:
归纳小结
1.熟记特殊三角函数表
:
30°
45°
60°
sinα
cosα
tanα
2.学习反思
要熟记上表,灵活运用
强化训练
1.已知α为锐角,且
则α的取值范围是(
)
A.0°<α<30°
B.60°<α<90
C.45°<α<60°
D.30°<α<45°
C
2.已知:Rt△ABC中,∠C=90°cosA=
,AB=15,
则AC的长是(
)
A.3
B.6
C.9
D.12
C
强化训练
3.下列各式中不正确的是(
)
A.
B.sin30°+cos30°=1
C.sin35°=cos55°
D.tan45°>sin45°
B
强化训练
4.计算2sin30°-2cos60°+tan45°的结果是(
)
A.2
B.
C.
D.1
D
5.在△ABC中,∠A、∠B都是锐角,且sinA=
,cosB=
,
则△ABC的形状是(
)
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不能确定
B
强化训练
6.在△ABC中,∠C为直角,不查表解下列问题:
(1)已知a=5,
∠B=60°.求b;
解:
(2)已知a=
,b=
,求∠A.
解:
28
28.1
锐角三角函数
第3课时
特殊的三角函数值
锐角三角函数
学习目标
1.理解特殊角的三角函数值的由来.
2.熟记30°,45°,60°的三角函数;
3.根据一个特殊角的三角函数值说出这个角.
导入新课
A
B
C
∠
A的对边
∠A的邻边
斜边
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
斜边
∠A的对边
sinA
斜边
探究新知
活动
1
两块三角尺中有几个不同的锐角?
这几个锐角的正弦值、
余弦值和正切值各是多少?
30°
60°
45°
45°
探究新知
解:
设30°所对的直角边长为a,那么斜边长为2a.
另一条直角边长=
30°
探究新知
60°
45°
设两条直角边长为a,则斜边长=
探究新知
知识点一
特殊角三角函数
探究新知
30°
45°
60°
sinα
cosα
tanα
仔细观察,说说你发现这张表有哪些规律.
探究新知
求下列各式的值:
教材例3
(1)cos260°+sin260°
解:
cos260°+sin260°
=1
解:
=0
(2)
应用新知
练一练
1.在Rt△ABC中,∠C为直角,sinA=
,则cosB的值是(
)
A.
B.
C.1
D.
D
2.在Rt△ABC中,
2sin(α+20°)=
,则锐角α的度数是(
)
A.60°
B.80°
C.40°
D.以上结论都不对
C
应用新知
知识点二
利用特殊角三角函数
进行简单计算
应用新知
例4
A
B
C
解:
在图中,
∵
∠A=______
45°
求∠A的度数.
如图,在Rt△ABC中,∠C=90°,AB=
,BC=
α=
_____
应用新知
(2)如图,AO
是圆锥的高,OB
是底面半径,AO=
OB,
求α的度数.
60°
解:
在图中,
∵
∴
当A,B,为锐角时,若A≠B,
则sinA=sinB,cosA≠cosB,tanA=tanB.
应用新知
练一练—
计算
(1)2
cos45°
解:
(2)1-2sin30°cos30°.
解:
归纳小结
1.熟记特殊三角函数表
:
30°
45°
60°
sinα
cosα
tanα
2.学习反思
要熟记上表,灵活运用
强化训练
1.已知α为锐角,且
则α的取值范围是(
)
A.0°<α<30°
B.60°<α<90
C.45°<α<60°
D.30°<α<45°
C
2.已知:Rt△ABC中,∠C=90°cosA=
,AB=15,
则AC的长是(
)
A.3
B.6
C.9
D.12
C
强化训练
3.下列各式中不正确的是(
)
A.
B.sin30°+cos30°=1
C.sin35°=cos55°
D.tan45°>sin45°
B
强化训练
4.计算2sin30°-2cos60°+tan45°的结果是(
)
A.2
B.
C.
D.1
D
5.在△ABC中,∠A、∠B都是锐角,且sinA=
,cosB=
,
则△ABC的形状是(
)
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不能确定
B
强化训练
6.在△ABC中,∠C为直角,不查表解下列问题:
(1)已知a=5,
∠B=60°.求b;
解:
(2)已知a=
,b=
,求∠A.
解:
