人教版高三物理选修3-5第16章动量守恒动律复习第三课时课件(共26张PPT)
文档属性
| 名称 | 人教版高三物理选修3-5第16章动量守恒动律复习第三课时课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 621.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-22 16:09:50 | ||
图片预览







文档简介
(共26张PPT)
第三课时
碰撞、反冲、爆炸问题
第十六章
动量守恒定律
知识清单
考点一、碰撞
1.碰撞特点
(1)碰撞时间非常短,可以忽略不计.
(2)碰撞过程中内力往往远大于外力,系统所受外力可忽略,所以系统的动量守恒.
2.碰撞需满足的三个条件
(1)动量守恒,即p1+p2=p1′+p2′.
(2)动能不增加,即Ek1+Ek2≥Ek1′+Ek2′.
(3)速度要符合情景:碰撞后,原来在前面的物体的速度一定增大,且原来在前面的物体的速度大于或等于原来在后面的物体的速度,即v前′≥v后′,否则碰撞不会结束.
考点巧讲
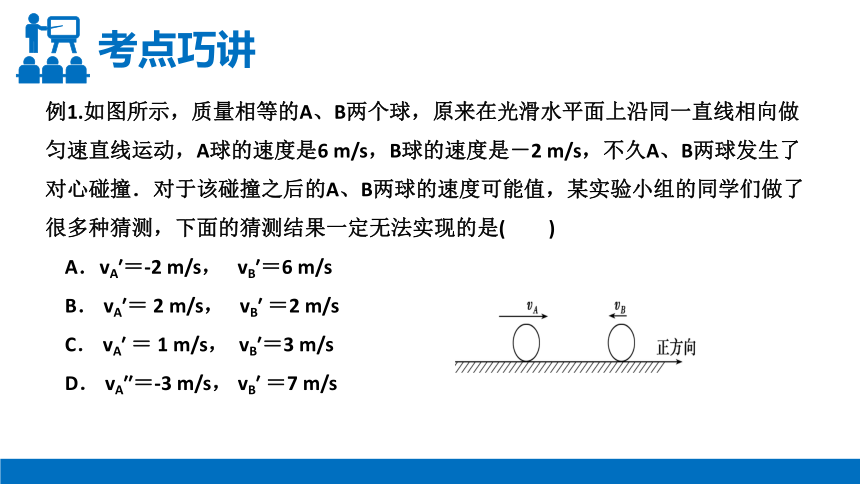
例1.如图所示,质量相等的A、B两个球,原来在光滑水平面上沿同一直线相向做匀速直线运动,A球的速度是6
m/s,B球的速度是-2
m/s,不久A、B两球发生了对心碰撞.对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的猜测结果一定无法实现的是( )
A.vA′=-2
m/s,
vB′=6
m/s
B.
vA′=
2
m/s,
vB′
=2
m/s
C.
vA′
=
1
m/s,
vB′=3
m/s
D.
vA′′=-3
m/s,
vB′
=7
m/s
考点巧讲
变式1.质量相等的A、B两球在光滑水平面上沿同一直线、同一方向运动,A球的动量是7
kg·m/s,B球的动量是5
kg·m/s,A球追上B球发生碰撞,则碰撞后A、B两球的动量可能值是( )
A.pA′=6
kg·m/s,
pB′=6
kg·m/s
B.
pA′
=3
kg·m/s,
pB′
=9
kg·m/s
C.
pA′
=-2
kg·m/s,
pB′
=14
kg·m/s
D.
pA′
=-4
kg·m/s,
pB′
=17
kg·m/s
知识清单
3.三种碰撞类型
(1)弹性碰撞
动量守恒:
m1v1+m2v2=m1v1′+m2v2′
机械能守恒:m1v12+
m2v22
=
m1v1′2+
m2v2′2
当v2=0时,有v1′=,v2′=
即v1′=0,v2′=v1
推论:
质量相等,大小、材料完全相同的弹性小球发生弹性碰撞,碰后交换速度.
即v1′=v2,v2′=v1
知识清单
(2)非弹性碰撞
动量守恒:m1v1+m2v2=m1v1′+m2v2′
机械能减少,损失的机械能转化为内能:
|ΔEk|=Ek初-Ek末=Q
(3)完全非弹性碰撞
动量守恒:m1v1+m2v2=(m1+m2)v共
碰撞中机械能损失最多
:
|ΔEk|=
m1v12+
m2v22
-
(m1+m2)v共2
种 类
特 点
弹性碰撞
动量守恒,机械能守恒
非弹性碰撞
动量守恒,机械能有损失
完全非弹性碰撞(合为一体)
动量守恒,机械能损失最大
考点巧讲
例2.如图所示,在光滑水平面上停放质量为m装有弧形槽的小车.现有一质量也为m的小球以v0的水平速度沿切线水平的槽口向小车滑去(不计摩擦),到达某一高度后,小球又返回小车右端,则( )
A.小球在小车上到达最高点时的速度大小为
B.小球离车后,对地将向右做平抛运动
C.小球离车后,对地将做自由落体运动
D.此过程中小球对车做的功为
mv02
考点巧讲
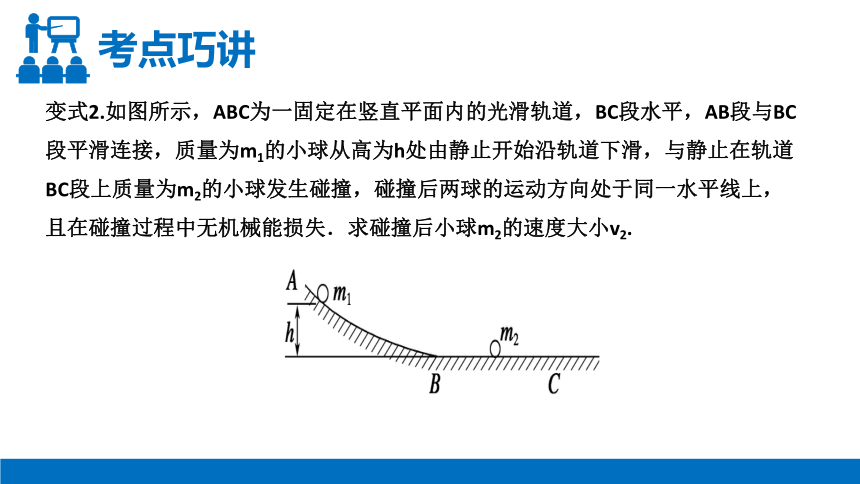
变式2.如图所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接,质量为m1的小球从高为h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为m2的小球发生碰撞,碰撞后两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失.求碰撞后小球m2的速度大小v2.
考点巧讲
例3.质量分别为300
g和200
g的两个物体在无摩擦的水平面上相向运动,速度分别为50
cm/s和100
cm/s.
(1)如果两物体碰撞并粘合在一起,求它们共同的速度大小;
(2)求碰撞后损失的动能;
(3)如果碰撞是弹性碰撞,求两物体碰撞后的速度大小.
考点巧讲
变式3.如图所示,光滑水平直轨道上两滑块A、B用橡皮筋连接,A的质量为m.开始时橡皮筋松弛,B静止,给A向左的初速度v0.一段时间后,B与A同向运动发生碰撞并粘在一起.碰撞后的共同速度是碰撞前瞬间A的速度的两倍,也是碰撞前瞬间B的速度的一半.求:
(1)B的质量;
(2)碰撞过程中A、B系统机械能的损失.
知识清单
考点二、反冲运动
1.定义:一个静止的物体在内力的作用下分裂为两部分,一部分向某个方向运动,
另外一个部分必然向相反方向运动,这个现象叫反冲。?
2.特点:
Ⅰ.物体的不同部分在内力的作用下向相反方向运动。?
Ⅱ.在反冲运动中,系统的合外力一般不为零,但内力远大于外力,可认为反冲运动中
系统动量守恒。?
Ⅲ.在反冲运动中,由于有其他形式的能转变为机械能,机械能总量一般是增加的。
知识清单
3.讨论反冲运动时应注意的问题
(1)速度的相对性:解决反冲运动的问题时,有时遇到的速度是相互作用的两物体的相对速度。由于动量守恒定律中要求速度为相对同一参考系的速度,即对地的速度。因此应先将相对速度转换成对地的速度后,再列动量守恒定律方程。
(2)变质量问题:在反冲运动中还常遇到变质量物体的运动,如在火箭的运动过程中,随着燃料的消耗,火箭本身的质量不断减小,此时必须取火箭本身和在相互作用的短时间内喷出的所有气体为研究对象。
例:(2017全国卷Ⅰ,14)将质量为1.00
kg的模型火箭点火升空,50
g
燃烧的燃气以大小为600
m/s的速度从火箭喷口在很短时间内喷出。在燃气喷出后的瞬间,火箭的动量大小为(喷出过程中重力和空气阻力可忽略)( )。
A.30
kg·m/s B.5.7×102
kg·m/s
C.6.0×102
kg·m/s
D.6.3×102
kg·m/s
A
知识清单
(3)反冲现象的应用和防止
Ⅰ.应用:反击式水轮机是使水从转轮的叶片中流出,由于反冲而使转轮旋转,从而带动发电机发电,火箭、喷气式飞机是靠喷出气流的反冲作用而获得巨大的推力,等等。
Ⅱ.避免有害的反冲运动。
例:(2018江苏南通第二次质量调研模拟)(多选)下列属于反冲运动的是(
)。
A.喷气式飞机的运动
B.氢气球的上升
C.火箭的运动
D.反击式水轮机的运动
ACD
4.
反冲运动中的“人船模型”
考点巧讲
Ⅰ.“人船模型”问题的特征
两个原来静止的物体发生相互作用时,若所受外力的矢量和为零,则动量守恒,在相互作用的过程中,任一时刻两物体的速度大小之比等于质量的反比。这样的问题归为“人船模型”问题。
Ⅱ.人船模型的特点
(1)两物体满足动量守恒定律:m1v1-m2v2=0。
(2)运动特点:人动船动,人静船静,人快船快,人慢船慢,人左船右;人船位移比等于它们质量的反比;人船平均速度(瞬时速度)比等于它们质量的反比,即
。
(3)应用此关系时要注意一个问题:v1、v2和x1、x2一般都是相对地面而言的。
知识清单
Ⅲ.处理“人船模型”问题的关键
(1)利用动量守恒,确定两物体速度关系,再确定两物体通过的位移的关系。
(2)解题时要画出各物体的位移关系草图,找出各长度间的关系。
(3)适用条件:
“人船模型”是利用平均动量守恒求解的一类问题。适用条件是:
①系统由两个物体组成且相互作用前静止,系统总动量守恒。
②在系统内发生相对运动的过程中至少有一个方向的动量守恒,注意两物体的位移是相对同一参考系的位移。
这一模型,还可进一步推广到其他类似的现象中,解决大量的实际问题,例如人沿着静止在空中的热气球下面的软梯滑下或攀上,求气球上升或下降高度的问题;小球沿弧形槽滑下,求弧形槽移动距离的问题等。
考点巧讲
例4.某人站在静止于水面的船上,从某时刻开始,人从船头走向船尾,水的阻力不计,则( )
A.人匀速运动,船则匀速后退,两者的速度大小与它们的质量成反比
B.人走到船尾不再走动,船也停止不动
C.不管人如何走动,人在行走的任意时刻人和船的速度方向总是相反,大小与它们的质量成反比
D.船的运动情况与人行走的情况无关
考点巧讲
变式4.如图所示,船静止在平静的水面上,船前舱有一抽水机,抽水机把前舱的水均匀的抽往后舱,不计水的阻力,下列说法中正确的是( )
A.若前后舱是分开的,则前舱将向后加速运动
B.若前后舱是分开的,则前舱将向前加速运动
C.若前后舱不分开,则船将向后加速运动
D.若前后舱不分开,则船将向前加速运动
考点巧讲
变式5.质量为m、半径为R的小球,放在半径为2R、质量为2m的大空心球内,大球开始静止在光滑水平面上。当小球从如图所示的位置无初速度沿内壁滚到最低点时,大球移动的距离为( )。
考点巧讲
考点巧讲
2.小车静置在光滑水平面上,站在车上一端的人练习打靶,靶装在车上的另一端,如图所示(小圆点表示枪口).已知车、人、枪和靶的总质量为M(不含子弹),每颗子弹质量为m,共n发.打靶时,每发子弹都打中靶且留在靶里,并等前一发打入靶中后,再打下一发.若枪口到靶的距离为d,待打完n发子弹后,小车移动的距离为________.
考点巧讲
考点巧讲
4.平板车停在水平光滑的轨道上,平板车上有一人从固定在车上的货厢边沿水平方向顺着轨道方向跳出,落在平板车地板上的A点,距货厢水平距离为l=4
m,如图所示.人的质量为m,车连同货厢的质量为M=4m,货厢高度为h=1.25
m,求:人跳出后到落到地板上时车的反冲速度是多少?
C
考点巧讲
知识清单
考点三
爆炸问题
解决爆炸类问题时,要抓住以下三个特征:
1.动量守恒:由于爆炸是在极短的时间内完成的,爆炸的物体间的相互作用力远大于受到的外力,所以在爆炸过程中,系统的动量守恒。
2.动能增加:在爆炸过程中,由于有其他形式的能量(如化学能)转化为动能,因此爆炸后系统的总动能增加。
3.位置不变:爆炸的时间极短,因而作用过程中,物体产生的位移很小,一般可忽略不计,可以认为爆炸后,物体仍然从爆炸的位置以新的动量开始运动。
例
答案
考点巧讲
作业:
1.整理学案三;
2.完成学案四。
第三课时
碰撞、反冲、爆炸问题
第十六章
动量守恒定律
知识清单
考点一、碰撞
1.碰撞特点
(1)碰撞时间非常短,可以忽略不计.
(2)碰撞过程中内力往往远大于外力,系统所受外力可忽略,所以系统的动量守恒.
2.碰撞需满足的三个条件
(1)动量守恒,即p1+p2=p1′+p2′.
(2)动能不增加,即Ek1+Ek2≥Ek1′+Ek2′.
(3)速度要符合情景:碰撞后,原来在前面的物体的速度一定增大,且原来在前面的物体的速度大于或等于原来在后面的物体的速度,即v前′≥v后′,否则碰撞不会结束.
考点巧讲
例1.如图所示,质量相等的A、B两个球,原来在光滑水平面上沿同一直线相向做匀速直线运动,A球的速度是6
m/s,B球的速度是-2
m/s,不久A、B两球发生了对心碰撞.对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的猜测结果一定无法实现的是( )
A.vA′=-2
m/s,
vB′=6
m/s
B.
vA′=
2
m/s,
vB′
=2
m/s
C.
vA′
=
1
m/s,
vB′=3
m/s
D.
vA′′=-3
m/s,
vB′
=7
m/s
考点巧讲
变式1.质量相等的A、B两球在光滑水平面上沿同一直线、同一方向运动,A球的动量是7
kg·m/s,B球的动量是5
kg·m/s,A球追上B球发生碰撞,则碰撞后A、B两球的动量可能值是( )
A.pA′=6
kg·m/s,
pB′=6
kg·m/s
B.
pA′
=3
kg·m/s,
pB′
=9
kg·m/s
C.
pA′
=-2
kg·m/s,
pB′
=14
kg·m/s
D.
pA′
=-4
kg·m/s,
pB′
=17
kg·m/s
知识清单
3.三种碰撞类型
(1)弹性碰撞
动量守恒:
m1v1+m2v2=m1v1′+m2v2′
机械能守恒:m1v12+
m2v22
=
m1v1′2+
m2v2′2
当v2=0时,有v1′=,v2′=
即v1′=0,v2′=v1
推论:
质量相等,大小、材料完全相同的弹性小球发生弹性碰撞,碰后交换速度.
即v1′=v2,v2′=v1
知识清单
(2)非弹性碰撞
动量守恒:m1v1+m2v2=m1v1′+m2v2′
机械能减少,损失的机械能转化为内能:
|ΔEk|=Ek初-Ek末=Q
(3)完全非弹性碰撞
动量守恒:m1v1+m2v2=(m1+m2)v共
碰撞中机械能损失最多
:
|ΔEk|=
m1v12+
m2v22
-
(m1+m2)v共2
种 类
特 点
弹性碰撞
动量守恒,机械能守恒
非弹性碰撞
动量守恒,机械能有损失
完全非弹性碰撞(合为一体)
动量守恒,机械能损失最大
考点巧讲
例2.如图所示,在光滑水平面上停放质量为m装有弧形槽的小车.现有一质量也为m的小球以v0的水平速度沿切线水平的槽口向小车滑去(不计摩擦),到达某一高度后,小球又返回小车右端,则( )
A.小球在小车上到达最高点时的速度大小为
B.小球离车后,对地将向右做平抛运动
C.小球离车后,对地将做自由落体运动
D.此过程中小球对车做的功为
mv02
考点巧讲
变式2.如图所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接,质量为m1的小球从高为h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为m2的小球发生碰撞,碰撞后两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失.求碰撞后小球m2的速度大小v2.
考点巧讲
例3.质量分别为300
g和200
g的两个物体在无摩擦的水平面上相向运动,速度分别为50
cm/s和100
cm/s.
(1)如果两物体碰撞并粘合在一起,求它们共同的速度大小;
(2)求碰撞后损失的动能;
(3)如果碰撞是弹性碰撞,求两物体碰撞后的速度大小.
考点巧讲
变式3.如图所示,光滑水平直轨道上两滑块A、B用橡皮筋连接,A的质量为m.开始时橡皮筋松弛,B静止,给A向左的初速度v0.一段时间后,B与A同向运动发生碰撞并粘在一起.碰撞后的共同速度是碰撞前瞬间A的速度的两倍,也是碰撞前瞬间B的速度的一半.求:
(1)B的质量;
(2)碰撞过程中A、B系统机械能的损失.
知识清单
考点二、反冲运动
1.定义:一个静止的物体在内力的作用下分裂为两部分,一部分向某个方向运动,
另外一个部分必然向相反方向运动,这个现象叫反冲。?
2.特点:
Ⅰ.物体的不同部分在内力的作用下向相反方向运动。?
Ⅱ.在反冲运动中,系统的合外力一般不为零,但内力远大于外力,可认为反冲运动中
系统动量守恒。?
Ⅲ.在反冲运动中,由于有其他形式的能转变为机械能,机械能总量一般是增加的。
知识清单
3.讨论反冲运动时应注意的问题
(1)速度的相对性:解决反冲运动的问题时,有时遇到的速度是相互作用的两物体的相对速度。由于动量守恒定律中要求速度为相对同一参考系的速度,即对地的速度。因此应先将相对速度转换成对地的速度后,再列动量守恒定律方程。
(2)变质量问题:在反冲运动中还常遇到变质量物体的运动,如在火箭的运动过程中,随着燃料的消耗,火箭本身的质量不断减小,此时必须取火箭本身和在相互作用的短时间内喷出的所有气体为研究对象。
例:(2017全国卷Ⅰ,14)将质量为1.00
kg的模型火箭点火升空,50
g
燃烧的燃气以大小为600
m/s的速度从火箭喷口在很短时间内喷出。在燃气喷出后的瞬间,火箭的动量大小为(喷出过程中重力和空气阻力可忽略)( )。
A.30
kg·m/s B.5.7×102
kg·m/s
C.6.0×102
kg·m/s
D.6.3×102
kg·m/s
A
知识清单
(3)反冲现象的应用和防止
Ⅰ.应用:反击式水轮机是使水从转轮的叶片中流出,由于反冲而使转轮旋转,从而带动发电机发电,火箭、喷气式飞机是靠喷出气流的反冲作用而获得巨大的推力,等等。
Ⅱ.避免有害的反冲运动。
例:(2018江苏南通第二次质量调研模拟)(多选)下列属于反冲运动的是(
)。
A.喷气式飞机的运动
B.氢气球的上升
C.火箭的运动
D.反击式水轮机的运动
ACD
4.
反冲运动中的“人船模型”
考点巧讲
Ⅰ.“人船模型”问题的特征
两个原来静止的物体发生相互作用时,若所受外力的矢量和为零,则动量守恒,在相互作用的过程中,任一时刻两物体的速度大小之比等于质量的反比。这样的问题归为“人船模型”问题。
Ⅱ.人船模型的特点
(1)两物体满足动量守恒定律:m1v1-m2v2=0。
(2)运动特点:人动船动,人静船静,人快船快,人慢船慢,人左船右;人船位移比等于它们质量的反比;人船平均速度(瞬时速度)比等于它们质量的反比,即
。
(3)应用此关系时要注意一个问题:v1、v2和x1、x2一般都是相对地面而言的。
知识清单
Ⅲ.处理“人船模型”问题的关键
(1)利用动量守恒,确定两物体速度关系,再确定两物体通过的位移的关系。
(2)解题时要画出各物体的位移关系草图,找出各长度间的关系。
(3)适用条件:
“人船模型”是利用平均动量守恒求解的一类问题。适用条件是:
①系统由两个物体组成且相互作用前静止,系统总动量守恒。
②在系统内发生相对运动的过程中至少有一个方向的动量守恒,注意两物体的位移是相对同一参考系的位移。
这一模型,还可进一步推广到其他类似的现象中,解决大量的实际问题,例如人沿着静止在空中的热气球下面的软梯滑下或攀上,求气球上升或下降高度的问题;小球沿弧形槽滑下,求弧形槽移动距离的问题等。
考点巧讲
例4.某人站在静止于水面的船上,从某时刻开始,人从船头走向船尾,水的阻力不计,则( )
A.人匀速运动,船则匀速后退,两者的速度大小与它们的质量成反比
B.人走到船尾不再走动,船也停止不动
C.不管人如何走动,人在行走的任意时刻人和船的速度方向总是相反,大小与它们的质量成反比
D.船的运动情况与人行走的情况无关
考点巧讲
变式4.如图所示,船静止在平静的水面上,船前舱有一抽水机,抽水机把前舱的水均匀的抽往后舱,不计水的阻力,下列说法中正确的是( )
A.若前后舱是分开的,则前舱将向后加速运动
B.若前后舱是分开的,则前舱将向前加速运动
C.若前后舱不分开,则船将向后加速运动
D.若前后舱不分开,则船将向前加速运动
考点巧讲
变式5.质量为m、半径为R的小球,放在半径为2R、质量为2m的大空心球内,大球开始静止在光滑水平面上。当小球从如图所示的位置无初速度沿内壁滚到最低点时,大球移动的距离为( )。
考点巧讲
考点巧讲
2.小车静置在光滑水平面上,站在车上一端的人练习打靶,靶装在车上的另一端,如图所示(小圆点表示枪口).已知车、人、枪和靶的总质量为M(不含子弹),每颗子弹质量为m,共n发.打靶时,每发子弹都打中靶且留在靶里,并等前一发打入靶中后,再打下一发.若枪口到靶的距离为d,待打完n发子弹后,小车移动的距离为________.
考点巧讲
考点巧讲
4.平板车停在水平光滑的轨道上,平板车上有一人从固定在车上的货厢边沿水平方向顺着轨道方向跳出,落在平板车地板上的A点,距货厢水平距离为l=4
m,如图所示.人的质量为m,车连同货厢的质量为M=4m,货厢高度为h=1.25
m,求:人跳出后到落到地板上时车的反冲速度是多少?
C
考点巧讲
知识清单
考点三
爆炸问题
解决爆炸类问题时,要抓住以下三个特征:
1.动量守恒:由于爆炸是在极短的时间内完成的,爆炸的物体间的相互作用力远大于受到的外力,所以在爆炸过程中,系统的动量守恒。
2.动能增加:在爆炸过程中,由于有其他形式的能量(如化学能)转化为动能,因此爆炸后系统的总动能增加。
3.位置不变:爆炸的时间极短,因而作用过程中,物体产生的位移很小,一般可忽略不计,可以认为爆炸后,物体仍然从爆炸的位置以新的动量开始运动。
例
答案
考点巧讲
作业:
1.整理学案三;
2.完成学案四。
