人教版九年级下册数学:28.1锐角三角函数 课件 (共24张PPT)
文档属性
| 名称 | 人教版九年级下册数学:28.1锐角三角函数 课件 (共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 483.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-22 19:04:44 | ||
图片预览


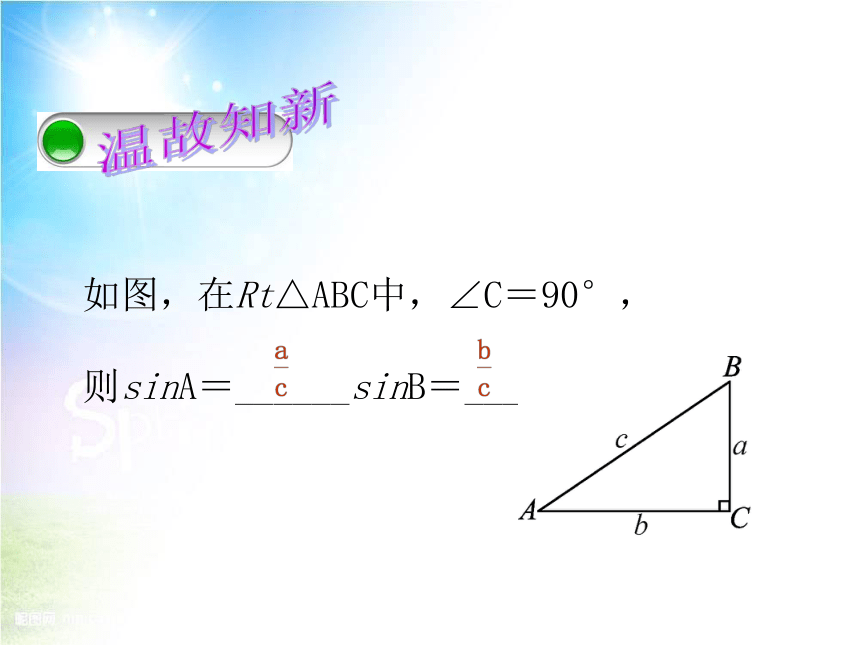



文档简介
(共24张PPT)
锐角三角函数(2)余弦和正切
正弦的定义:
在Rt△ABC中,∠C=90°,我们
把锐角A的对边与斜边的比叫做∠A的
正弦。记作sinA,即
如图,在Rt△ABC中,∠C=90°,
则sinA=______sinB=________
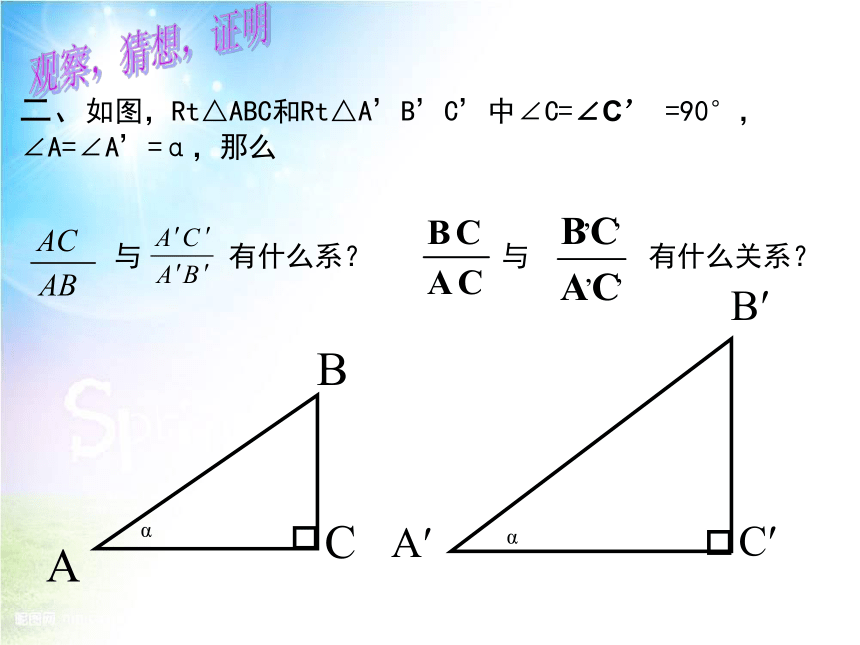
二、如图,Rt△ABC和Rt△A’B’C’中∠C=∠C’
=90°,∠A=∠A’=α,那么
与
有什么系?
α
α
与
有什么关系?
三角函数的定义:
锐角的正弦、余弦、正切统称为锐角三角函数。
对于锐角A的每一个确定的值sinA有唯一确定的值与它对应,所以sinA是A的函数。同样地,cosA、tanA也是A的函数。
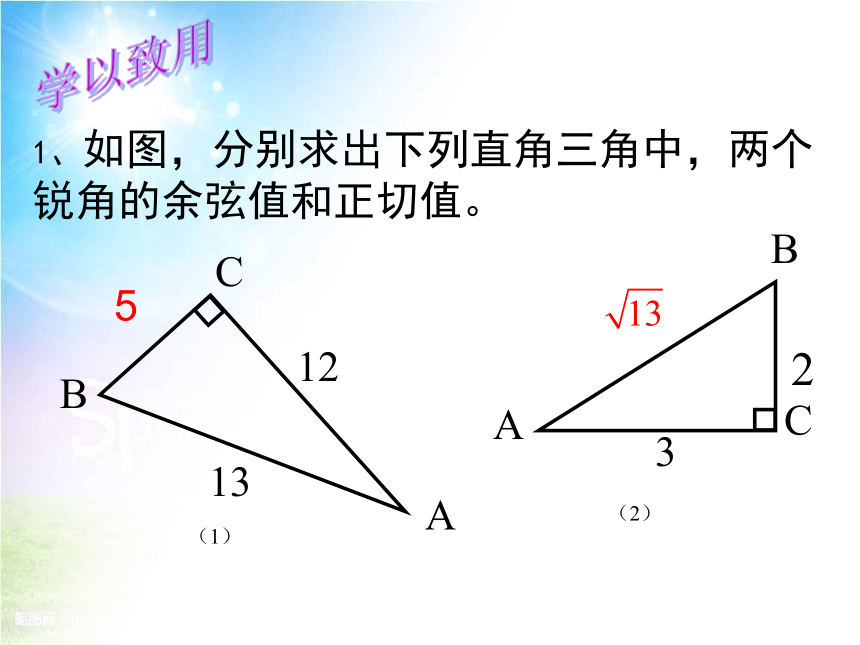
1、如图,分别求出下列直角三角中,两个锐角的余弦值和正切值。
13
12
(1)
5
2.
在Rt△ABC中,如果各边长都扩大2倍,那么锐角A的正弦值、余弦值和正切值有什么变化?
解:设各边长分别为a、b、c,∠A的三个三角函数分别为
则扩大2倍后三边分别为2a、2b、2c
a
b
c
2a
2b
2c
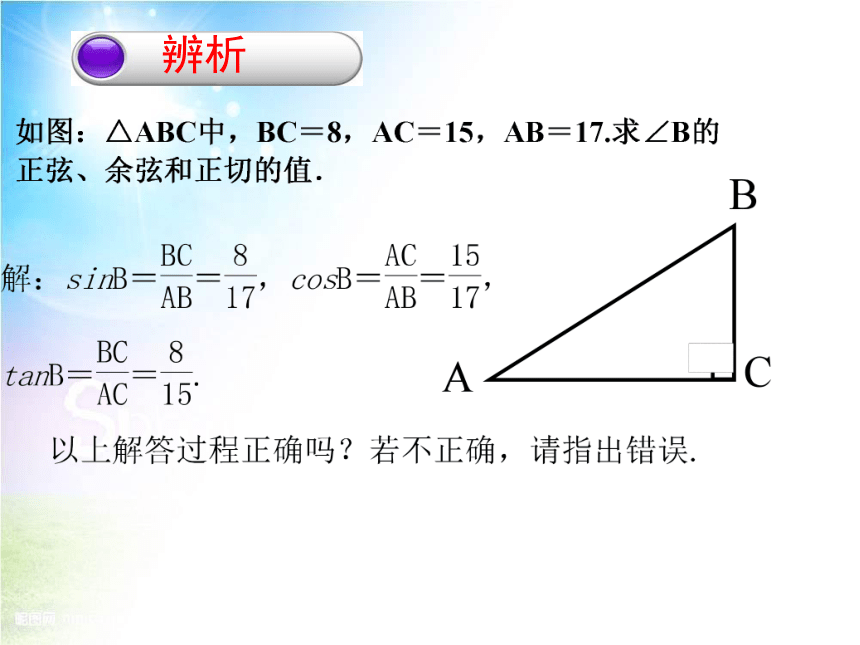
不正确.
错误一:没有指明△ABC是直角三角形;
错误二:错解中求的是∠A的正弦、余弦和正切值,而不是∠B的正弦、余弦和正切值
正解如下:
知识总结
1.任意锐角都有三角函数值,这个值只与锐角的度数有关系,与锐角所在三角形的大小和锐角的位置无关。
2.求锐角的三角函数值时要弄清是哪两条边的比值,求值时要在直角三角形中.
如图,在Rt△ABC中,∠C=90°,
AB=10,tanA=
,求sinA、cosA的值。
1.如图,在Rt△ABC中,∠C=90°,BC=6,sinA=
,
求cosA、tanB的值.
解:∵
又
在Rt△ABC中
2、如图,在Rt△ABC中,∠C=90°,cosA=
,
求sinA、tanA的值.
∵
设AC=15k,则AB=17k
所以
解:如图在Rt△ABC中,
3.已知锐角α的始边在x轴的正半轴上(顶点在原点),终边上一点P的坐标为(1,2),求角α的三个三角函数值。
P(1,2)
α
A
1
2
√5
∟
1.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,
求tan∠OBC的值
D
2.矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D恰好落在AB边上,求tan∠AFE的值.
3.如图,设P是等边三角形ABC内的一点,PA=1,PB=2,PC=√5
将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P′外,则sin∠PCP′的值是______(不取近似值).
1.如图,以O?为圆心,半径为1?的弧交坐标轴于A,B?两点,P是弧AB上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是(??)
A(sinα,sinα)??
B(cosα,cosα)?
C(cosα,sinα)???
D(sinα,cosα)
2.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=3:5,AB=3,则AD的长为______.
3.如图,圆O的直径AB=8,AC=3CB,过C作AB的垂线交圆O于M,N两点,连结MB,则∠MBA的余弦值为?????.
1.余弦的定义:
2.正切的定义:
3.三角函数的定义:
[归纳]
1.任意锐角都有三角函数值,这个值只和锐角的度数
有关,与锐角所在三角形的大小,和锐角的位置无关。
2.锐角的三角函数值是两条边的比值,求值时要在直角
三角形中或者进行转化.
作业:
1、完成同步训练P61-62
1~11题
2、选做12题
锐角三角函数(2)余弦和正切
正弦的定义:
在Rt△ABC中,∠C=90°,我们
把锐角A的对边与斜边的比叫做∠A的
正弦。记作sinA,即
如图,在Rt△ABC中,∠C=90°,
则sinA=______sinB=________
二、如图,Rt△ABC和Rt△A’B’C’中∠C=∠C’
=90°,∠A=∠A’=α,那么
与
有什么系?
α
α
与
有什么关系?
三角函数的定义:
锐角的正弦、余弦、正切统称为锐角三角函数。
对于锐角A的每一个确定的值sinA有唯一确定的值与它对应,所以sinA是A的函数。同样地,cosA、tanA也是A的函数。
1、如图,分别求出下列直角三角中,两个锐角的余弦值和正切值。
13
12
(1)
5
2.
在Rt△ABC中,如果各边长都扩大2倍,那么锐角A的正弦值、余弦值和正切值有什么变化?
解:设各边长分别为a、b、c,∠A的三个三角函数分别为
则扩大2倍后三边分别为2a、2b、2c
a
b
c
2a
2b
2c
不正确.
错误一:没有指明△ABC是直角三角形;
错误二:错解中求的是∠A的正弦、余弦和正切值,而不是∠B的正弦、余弦和正切值
正解如下:
知识总结
1.任意锐角都有三角函数值,这个值只与锐角的度数有关系,与锐角所在三角形的大小和锐角的位置无关。
2.求锐角的三角函数值时要弄清是哪两条边的比值,求值时要在直角三角形中.
如图,在Rt△ABC中,∠C=90°,
AB=10,tanA=
,求sinA、cosA的值。
1.如图,在Rt△ABC中,∠C=90°,BC=6,sinA=
,
求cosA、tanB的值.
解:∵
又
在Rt△ABC中
2、如图,在Rt△ABC中,∠C=90°,cosA=
,
求sinA、tanA的值.
∵
设AC=15k,则AB=17k
所以
解:如图在Rt△ABC中,
3.已知锐角α的始边在x轴的正半轴上(顶点在原点),终边上一点P的坐标为(1,2),求角α的三个三角函数值。
P(1,2)
α
A
1
2
√5
∟
1.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,
求tan∠OBC的值
D
2.矩形ABCD中AB=10,BC=8,E为AD边上一点,沿CE将△CDE对折,使点D恰好落在AB边上,求tan∠AFE的值.
3.如图,设P是等边三角形ABC内的一点,PA=1,PB=2,PC=√5
将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P′外,则sin∠PCP′的值是______(不取近似值).
1.如图,以O?为圆心,半径为1?的弧交坐标轴于A,B?两点,P是弧AB上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是(??)
A(sinα,sinα)??
B(cosα,cosα)?
C(cosα,sinα)???
D(sinα,cosα)
2.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=3:5,AB=3,则AD的长为______.
3.如图,圆O的直径AB=8,AC=3CB,过C作AB的垂线交圆O于M,N两点,连结MB,则∠MBA的余弦值为?????.
1.余弦的定义:
2.正切的定义:
3.三角函数的定义:
[归纳]
1.任意锐角都有三角函数值,这个值只和锐角的度数
有关,与锐角所在三角形的大小,和锐角的位置无关。
2.锐角的三角函数值是两条边的比值,求值时要在直角
三角形中或者进行转化.
作业:
1、完成同步训练P61-62
1~11题
2、选做12题
