北师大版九年级下册数学:3.5 确定圆的条件 课件(共24张PPT)
文档属性
| 名称 | 北师大版九年级下册数学:3.5 确定圆的条件 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
北师大版数学九年级下册第3章第5节
§3.5
确定圆的条件
学习目标
1.知识与技能:
①理解不在同一直线上的三个点确定一个圆;
②掌握过不在同一直线上的三个点作圆的方法;
③了解三角形的外接圆、三角形的外心等概念,提高应用数学知识解决实际问题的能力。
2.过程与方法:经历不在同一直线上的三个点确定一个圆的探索过程,体会归纳、类比以及由特殊到一般的数学思想方法。
3.情感态度与价值观:在探索活动中培养学生勇于探究的学习品质,体会解决问题的策略,学会数学地思考。
情境导入:破镜重圆
问题1:小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是哪一块?
问题2:玻璃店里的师傅,要划出一块与原来大小一样的圆形玻璃,他只要知道圆的什么就可以了?为什么?
要确定一个圆关键是确定什么?
确定圆的圆心和半径
确定圆的条件
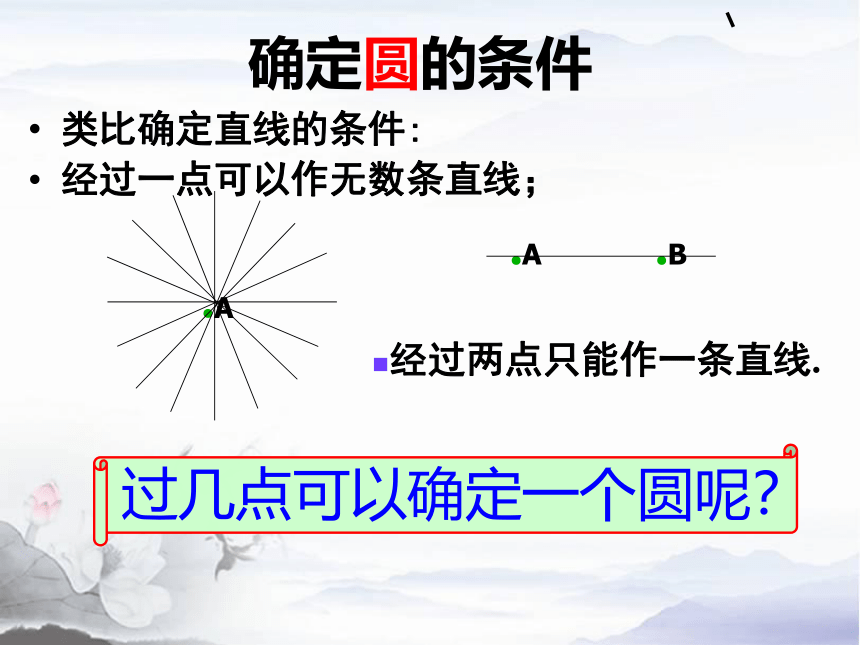
类比确定直线的条件:
经过一点可以作无数条直线;
经过两点只能作一条直线.
●A
●A
●B
过几点可以确定一个圆呢?
A
大胆尝试,自主探究
探索实践一:
1.经过点A能做出多少个圆?请尝试着画出来。
2.观察思考:过点A作圆的关键是什么?它的分布有规律吗?
确定圆的条件
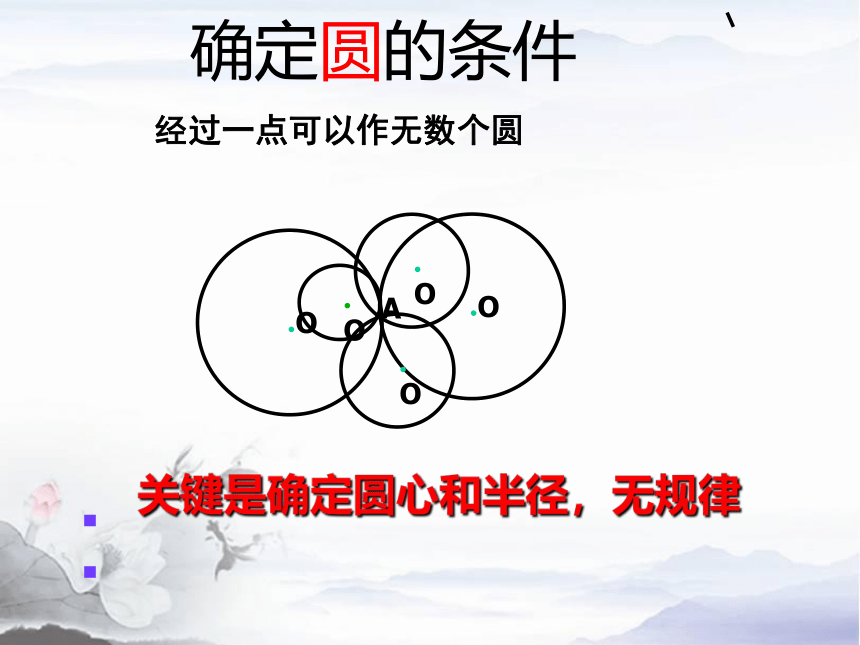
经过一点可以作无数个圆
●A
关键是确定圆心和半径,无规律
A
B
大胆尝试,自主探究
1.先猜想再实践,经过平面内的两个点A、B能作多少个圆?请再尝试着画出来。
2.观察思考:过平面内两点作圆的关键是什么?它的分布有规律吗?如何验证你的猜想?
探索实践二:
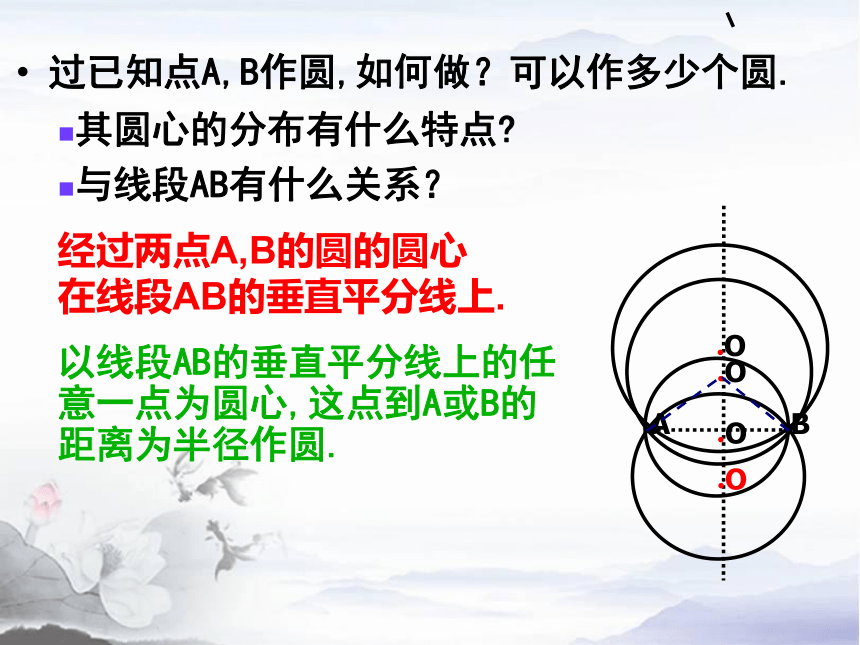
过已知点A,B作圆,如何做?可以作多少个圆.
以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.
其圆心的分布有什么特点?
与线段AB有什么关系?
●A
●B
●O
经过两点A,B的圆的圆心
在线段AB的垂直平分线上.
探索实践三:
1.经过不在同一条直线上的A,B,C三点能作圆吗?请先尝试探索,再在小组内交流,
说出你的做法。
A
B
C
2.经过这样的三点能作多少个圆?请继续尝试。
师生合作,共同探究
经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的⊙O存在
(1)圆心O到A、B、C三点距离
。
(2)连结AB、AC,
O点
应在AB的
;
同时O点也应在AC的
。
(3)圆心O应该是
N
M
F
E
相等
垂直平分线上
垂直平分线上
AB与AC垂直平分线的交点
已知:不在同一直线上的
三点A、B、C
求作:
⊙O使它经过点A、B、C
作法:1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆。
O
N
M
F
E
A
B
C
A
B
C
过如下三点能不能做圆?
为什么?
不在同一直线上的三点确定一个圆
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。
(二)知识拓展,再探新知
结合图形明确以下内容:
(1)三角形的外接圆和圆的内接三角形
(2)三角形的外心:
⑶你能总结出三角形的外心具有怎样
的性质吗?
经过三角形各个顶点的圆
叫做三角形的外接圆,外接圆
的圆心叫做三角形的外心,
这个三角形叫做圆的内接三角形。
外接圆
内接三角形
外心
三角形的外心
是三角形
的圆心
外接圆
是
的交点
三边垂直平分线
到
三顶点
的距离相等
现在你知道了怎样将一个如图所示的破损的玻璃碎片复原了吗?
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。
A
B
C
O
如图,请找出图中圆的圆心,并写出你找圆心的方法?
A
B
C
O
画出过以下三角形的顶点的圆
●O
C
A
B
┐
●O
●O
比较这三个三角形外心的位置,你有何发现?
(图一)
(图二)
(图三)
(三)知识梳理
我又掌握了哪些新知识?
2.
在探究过程中我又增进了哪些能力?
3.我的疑惑是·······
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定。
(2)经过一个已知点能作无数个圆!
(3)经过两个已知点A、B能作无数个圆!这些圆的圆心在线段AB的垂直平分线上。
(4)不在同一直线上的三个点确定一个圆。
(5)外接圆,外心的概念。
1、下列命题不正确的是
A.过一点有无数个圆.
B.过两点有无数个圆.
C.弦是圆的一部分.
D.不在同一直线上三点确定一个圆.
2、三角形的外心具有的性质是
A.到三边的距离相等.
B.到三个顶点的距离相等.
C.外心在三角形的外.
D.外心在三角形内.
当堂检测
当堂检测:
3.下列说法正确的是:(
)
A.经过三点一定可以作圆
B.三角形的外心就是这个三角形两边垂直平分线的交点
C.三角形的外心到三边的距离相等
D.等腰三角形的外心一定在这个三角形内部
4.如图,A、B、C三点表示三个工厂,要建立一个供水站,
使它到这三个工厂的距离相等,求作供水站的位置(不写作法,尺规作图,保留作图痕迹).
盛年不重来,
一日难再晨,
及时宜自勉,
岁月不待人.
课后寄语
北师大版数学九年级下册第3章第5节
§3.5
确定圆的条件
学习目标
1.知识与技能:
①理解不在同一直线上的三个点确定一个圆;
②掌握过不在同一直线上的三个点作圆的方法;
③了解三角形的外接圆、三角形的外心等概念,提高应用数学知识解决实际问题的能力。
2.过程与方法:经历不在同一直线上的三个点确定一个圆的探索过程,体会归纳、类比以及由特殊到一般的数学思想方法。
3.情感态度与价值观:在探索活动中培养学生勇于探究的学习品质,体会解决问题的策略,学会数学地思考。
情境导入:破镜重圆
问题1:小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是哪一块?
问题2:玻璃店里的师傅,要划出一块与原来大小一样的圆形玻璃,他只要知道圆的什么就可以了?为什么?
要确定一个圆关键是确定什么?
确定圆的圆心和半径
确定圆的条件
类比确定直线的条件:
经过一点可以作无数条直线;
经过两点只能作一条直线.
●A
●A
●B
过几点可以确定一个圆呢?
A
大胆尝试,自主探究
探索实践一:
1.经过点A能做出多少个圆?请尝试着画出来。
2.观察思考:过点A作圆的关键是什么?它的分布有规律吗?
确定圆的条件
经过一点可以作无数个圆
●A
关键是确定圆心和半径,无规律
A
B
大胆尝试,自主探究
1.先猜想再实践,经过平面内的两个点A、B能作多少个圆?请再尝试着画出来。
2.观察思考:过平面内两点作圆的关键是什么?它的分布有规律吗?如何验证你的猜想?
探索实践二:
过已知点A,B作圆,如何做?可以作多少个圆.
以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.
其圆心的分布有什么特点?
与线段AB有什么关系?
●A
●B
●O
经过两点A,B的圆的圆心
在线段AB的垂直平分线上.
探索实践三:
1.经过不在同一条直线上的A,B,C三点能作圆吗?请先尝试探索,再在小组内交流,
说出你的做法。
A
B
C
2.经过这样的三点能作多少个圆?请继续尝试。
师生合作,共同探究
经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的⊙O存在
(1)圆心O到A、B、C三点距离
。
(2)连结AB、AC,
O点
应在AB的
;
同时O点也应在AC的
。
(3)圆心O应该是
N
M
F
E
相等
垂直平分线上
垂直平分线上
AB与AC垂直平分线的交点
已知:不在同一直线上的
三点A、B、C
求作:
⊙O使它经过点A、B、C
作法:1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆。
O
N
M
F
E
A
B
C
A
B
C
过如下三点能不能做圆?
为什么?
不在同一直线上的三点确定一个圆
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。
(二)知识拓展,再探新知
结合图形明确以下内容:
(1)三角形的外接圆和圆的内接三角形
(2)三角形的外心:
⑶你能总结出三角形的外心具有怎样
的性质吗?
经过三角形各个顶点的圆
叫做三角形的外接圆,外接圆
的圆心叫做三角形的外心,
这个三角形叫做圆的内接三角形。
外接圆
内接三角形
外心
三角形的外心
是三角形
的圆心
外接圆
是
的交点
三边垂直平分线
到
三顶点
的距离相等
现在你知道了怎样将一个如图所示的破损的玻璃碎片复原了吗?
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。
A
B
C
O
如图,请找出图中圆的圆心,并写出你找圆心的方法?
A
B
C
O
画出过以下三角形的顶点的圆
●O
C
A
B
┐
●O
●O
比较这三个三角形外心的位置,你有何发现?
(图一)
(图二)
(图三)
(三)知识梳理
我又掌握了哪些新知识?
2.
在探究过程中我又增进了哪些能力?
3.我的疑惑是·······
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定。
(2)经过一个已知点能作无数个圆!
(3)经过两个已知点A、B能作无数个圆!这些圆的圆心在线段AB的垂直平分线上。
(4)不在同一直线上的三个点确定一个圆。
(5)外接圆,外心的概念。
1、下列命题不正确的是
A.过一点有无数个圆.
B.过两点有无数个圆.
C.弦是圆的一部分.
D.不在同一直线上三点确定一个圆.
2、三角形的外心具有的性质是
A.到三边的距离相等.
B.到三个顶点的距离相等.
C.外心在三角形的外.
D.外心在三角形内.
当堂检测
当堂检测:
3.下列说法正确的是:(
)
A.经过三点一定可以作圆
B.三角形的外心就是这个三角形两边垂直平分线的交点
C.三角形的外心到三边的距离相等
D.等腰三角形的外心一定在这个三角形内部
4.如图,A、B、C三点表示三个工厂,要建立一个供水站,
使它到这三个工厂的距离相等,求作供水站的位置(不写作法,尺规作图,保留作图痕迹).
盛年不重来,
一日难再晨,
及时宜自勉,
岁月不待人.
课后寄语
