《排列与组合》课件5(新人教A版选修2-3)
文档属性
| 名称 | 《排列与组合》课件5(新人教A版选修2-3) |  | |
| 格式 | rar | ||
| 文件大小 | 359.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-19 09:19:08 | ||
图片预览





文档简介
(共13张PPT)
引例
问题1 从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的方法?
第1步,确定参加上午活动的同学,从3人中任选1人有3种方法;
第2步,确定参加下午活动的同学,只能从余下的2人中选,有2种方法.
根据分步计数原理,共有:3×2=6 种不同的方法.
解决这个问题,需分2个步骤:
问题2:从a、b、c这3个字母中,每次取出2个按顺序排成一列,共有多少种不同的排法?并列出所有不同的排法。
这里的每一种排法就是一个排列。
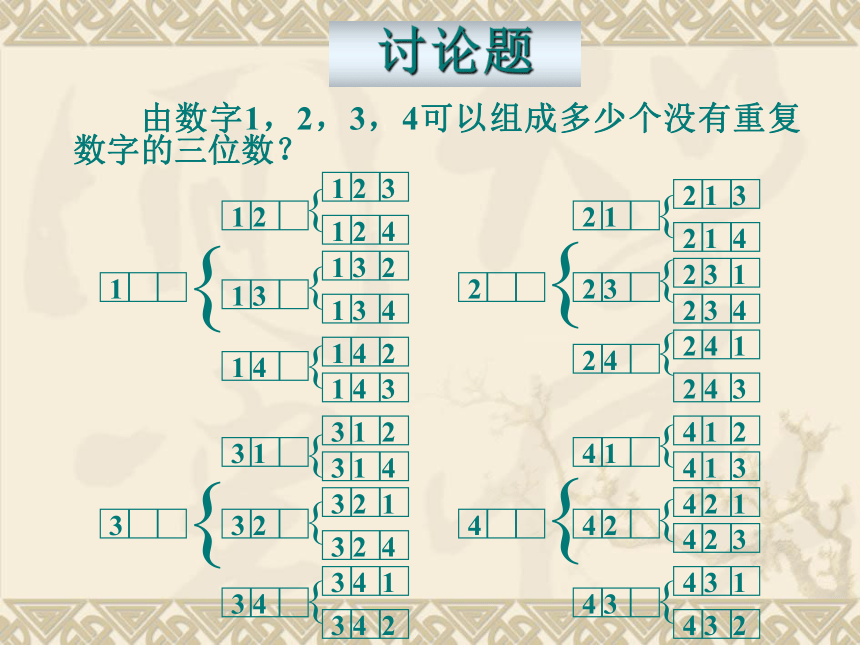
由数字1,2,3,4可以组成多少个没有重复数字的三位数?
1
1 2
1 4
1 3
1 2 3
1 2 4
{
{
{
{
1 3 2
1 3 4
1 4 2
1 4 3
3
{
3 1
3 2
3 4
{
{
{
3 1 2
3 1 4
3 2 1
3 2 4
3 4 1
3 4 2
2
{
2 1
2 3
2 4
{
{
{
2 1 3
2 1 4
2 3 1
2 3 4
2 4 1
2 4 3
4
{
4 1
4 2
4 3
{
{
{
4 1 2
4 1 3
4 2 1
4 2 3
4 3 1
4 3 2
讨论题
一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
排列的定义中包含两个基本内容:
一是“取出元素”;二是“按照一定顺序排列”.“一定顺序”就是与位置有关,这也是判断一个问题是不是排列问题的重要标志.
根据排列的定义,两个排列相同,当且仅当这两个排列的元素完全相同,而且元素的排列顺序也完全相同.
排列定义
如果两个排列所含的元素不完全一样,那么就可以肯定是不同的排列;如果两个排列所含的元素完全一样,但摆的顺序不同,那么也是不同的排列.
练习1.下列问题中哪些是排列问题?如果是在题后括号内打“√”,否则打“×”.
练习
(1)50位同学互通一封信,问共通多少封信? ( )
(2)50位同学互通一次电话,问共通多少次? ( )
(3)平面内有8个点,其中任意3点不共线,由这些点可得到多少条直线? ( )
(4)平面内有8个点,其中任意3点不共线,由这些点可得到多少条射线? ( )
(5)某商场有4个大门,若从一个门进去,购物后从一个门出来,有多少种不同的出入方式? ( )
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号 表示。
从n个不同元素中取出2个元素的排列数
是多少?
呢?
呢?
问题1 :从3个不同的元素中取出2个元素的排列
数,记为
问题2 : 从4个不同的元素中取出3个元素的排
列数,记为
1.排列数公式的特点:第一个因数是n,后面每一个因数比它前面一个因数少1,最后一个因数是n-m+1,共有m个因数.
阶乘变形
例2:化简:1!+2·2!+3·3!+…+n·n!
排列问题,是取出m个元素后,还要按一定的顺序排成一列,取出同样的m个元素,只要排列顺序不同,就视为完成这件事的两种不同的方法(两个不同的排列).
小结
由排列的定义可知,排列与元素的顺序有关,也就是说与位置有关的问题才能归结为排列问题.当元素较少时,可以根据排列的意义写出所有的排列.
引例
问题1 从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的方法?
第1步,确定参加上午活动的同学,从3人中任选1人有3种方法;
第2步,确定参加下午活动的同学,只能从余下的2人中选,有2种方法.
根据分步计数原理,共有:3×2=6 种不同的方法.
解决这个问题,需分2个步骤:
问题2:从a、b、c这3个字母中,每次取出2个按顺序排成一列,共有多少种不同的排法?并列出所有不同的排法。
这里的每一种排法就是一个排列。
由数字1,2,3,4可以组成多少个没有重复数字的三位数?
1
1 2
1 4
1 3
1 2 3
1 2 4
{
{
{
{
1 3 2
1 3 4
1 4 2
1 4 3
3
{
3 1
3 2
3 4
{
{
{
3 1 2
3 1 4
3 2 1
3 2 4
3 4 1
3 4 2
2
{
2 1
2 3
2 4
{
{
{
2 1 3
2 1 4
2 3 1
2 3 4
2 4 1
2 4 3
4
{
4 1
4 2
4 3
{
{
{
4 1 2
4 1 3
4 2 1
4 2 3
4 3 1
4 3 2
讨论题
一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
排列的定义中包含两个基本内容:
一是“取出元素”;二是“按照一定顺序排列”.“一定顺序”就是与位置有关,这也是判断一个问题是不是排列问题的重要标志.
根据排列的定义,两个排列相同,当且仅当这两个排列的元素完全相同,而且元素的排列顺序也完全相同.
排列定义
如果两个排列所含的元素不完全一样,那么就可以肯定是不同的排列;如果两个排列所含的元素完全一样,但摆的顺序不同,那么也是不同的排列.
练习1.下列问题中哪些是排列问题?如果是在题后括号内打“√”,否则打“×”.
练习
(1)50位同学互通一封信,问共通多少封信? ( )
(2)50位同学互通一次电话,问共通多少次? ( )
(3)平面内有8个点,其中任意3点不共线,由这些点可得到多少条直线? ( )
(4)平面内有8个点,其中任意3点不共线,由这些点可得到多少条射线? ( )
(5)某商场有4个大门,若从一个门进去,购物后从一个门出来,有多少种不同的出入方式? ( )
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号 表示。
从n个不同元素中取出2个元素的排列数
是多少?
呢?
呢?
问题1 :从3个不同的元素中取出2个元素的排列
数,记为
问题2 : 从4个不同的元素中取出3个元素的排
列数,记为
1.排列数公式的特点:第一个因数是n,后面每一个因数比它前面一个因数少1,最后一个因数是n-m+1,共有m个因数.
阶乘变形
例2:化简:1!+2·2!+3·3!+…+n·n!
排列问题,是取出m个元素后,还要按一定的顺序排成一列,取出同样的m个元素,只要排列顺序不同,就视为完成这件事的两种不同的方法(两个不同的排列).
小结
由排列的定义可知,排列与元素的顺序有关,也就是说与位置有关的问题才能归结为排列问题.当元素较少时,可以根据排列的意义写出所有的排列.
