二元一次不等式(组)与简单的线性
文档属性
| 名称 | 二元一次不等式(组)与简单的线性 |  | |
| 格式 | rar | ||
| 文件大小 | 206.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-19 16:49:19 | ||
图片预览


文档简介
(共29张PPT)
3.3.2简单的线性规划问题(二)
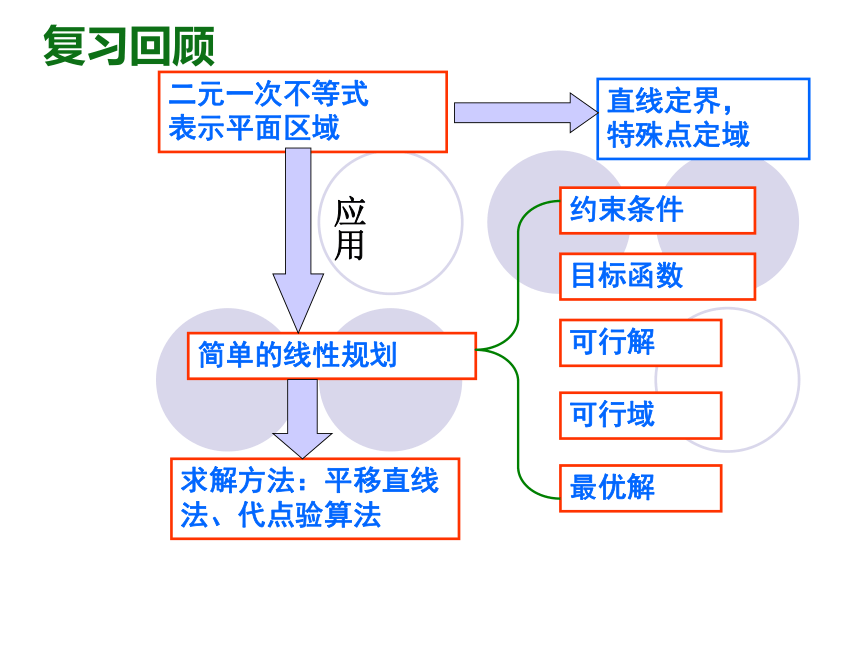
二元一次不等式 表示平面区域
直线定界, 特殊点定域
简单的线性规划
约束条件
目标函数
可行解
可行域
最优解
应用
求解方法:平移直线法、代点验算法
复习回顾
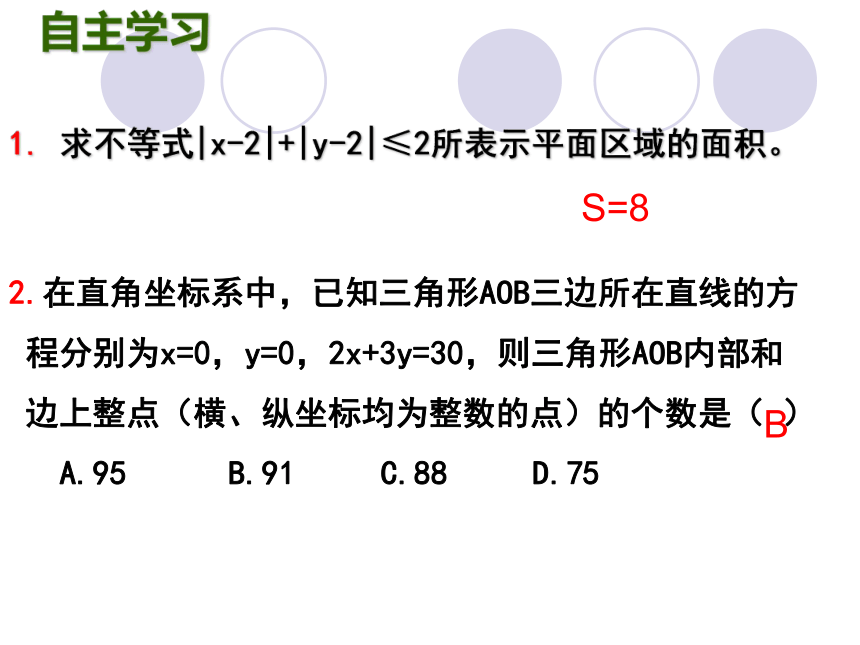
1. 求不等式|x-2|+|y-2|≤2所表示平面区域的面积。
2.在直角坐标系中,已知三角形AOB三边所在直线的方
程分别为x=0,y=0,2x+3y=30,则三角形AOB内部和
边上整点(横、纵坐标均为整数的点)的个数是( )
A.95 B.91 C.88 D.75
S=8
B
自主学习
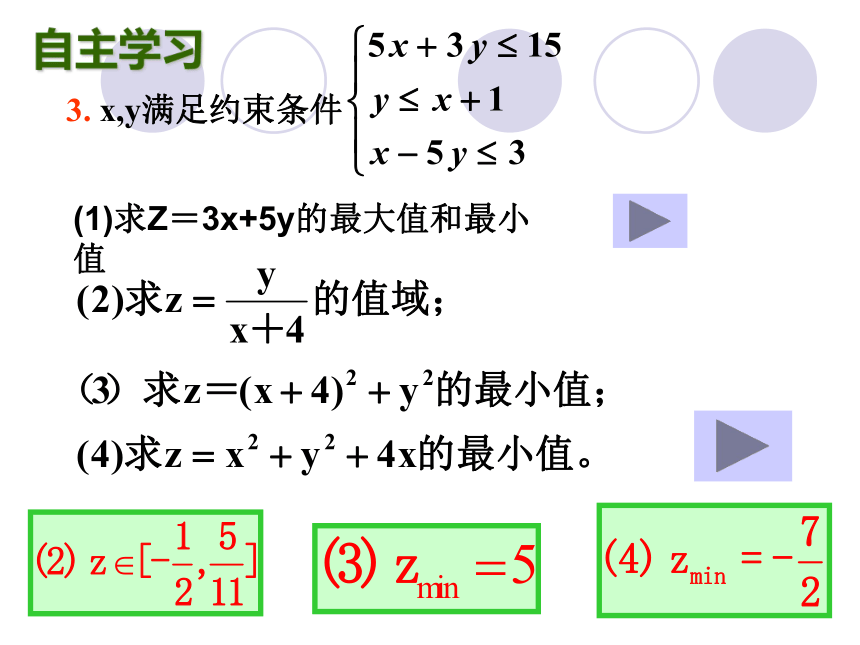
3. x,y满足约束条件
(1)求Z=3x+5y的最大值和最小值
自主学习
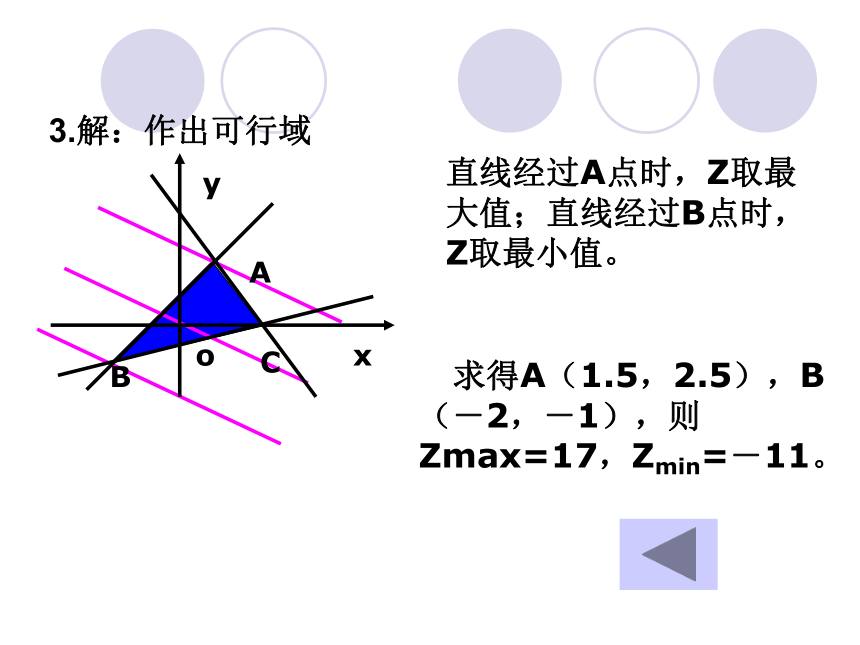
3.解:作出可行域
x
y
o
A
B
C
直线经过A点时,Z取最大值;直线经过B点时,Z取最小值。
求得A(1.5,2.5),B(-2,-1),则Zmax=17,Zmin=-11。
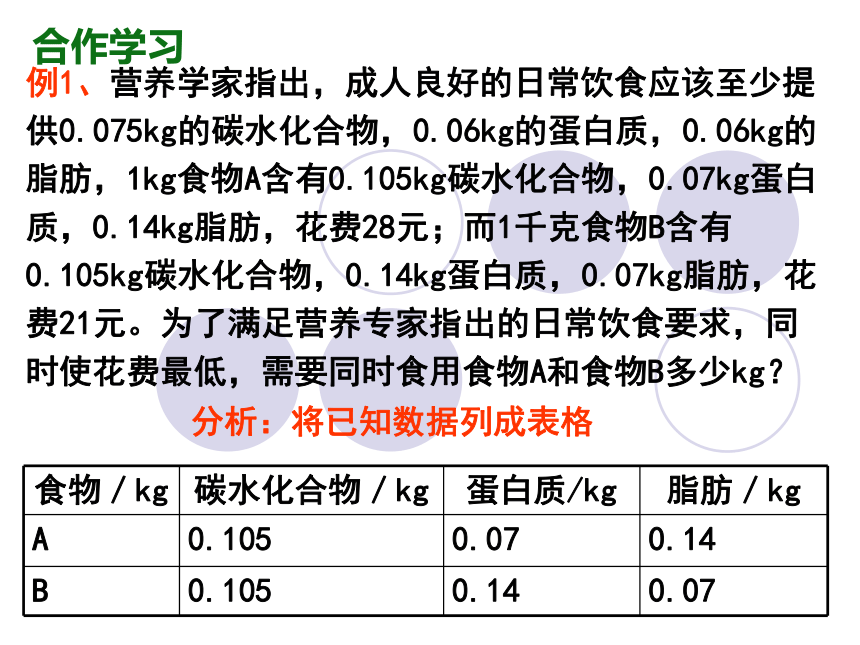
例1、营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1千克食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?
食物/kg 碳水化合物/kg 蛋白质/kg 脂肪/kg
A 0.105 0.07 0.14
B 0.105 0.14 0.07
分析:将已知数据列成表格
合作学习
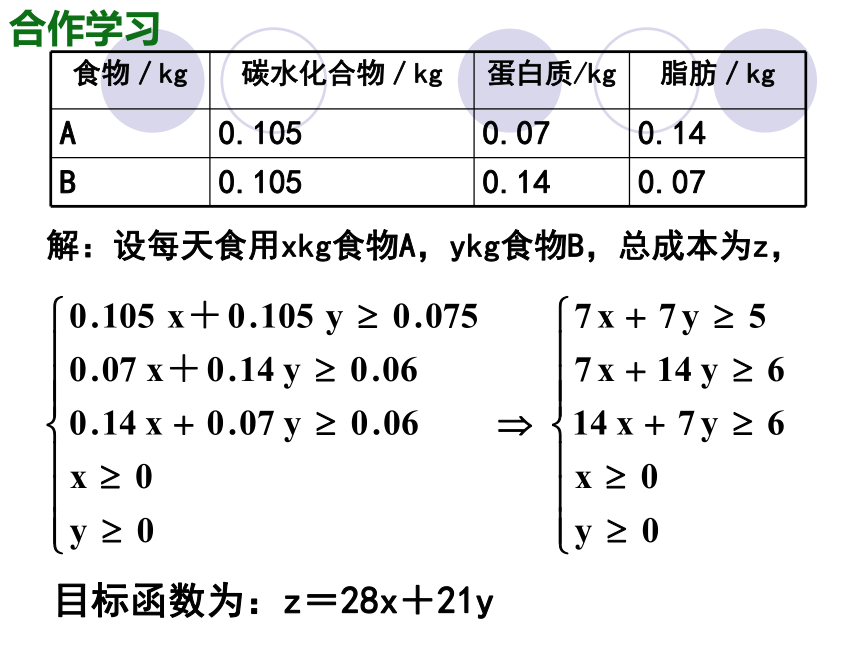
解:设每天食用xkg食物A,ykg食物B,总成本为z,
目标函数为:z=28x+21y
合作学习
食物/kg 碳水化合物/kg 蛋白质/kg 脂肪/kg
A 0.105 0.07 0.14
B 0.105 0.14 0.07
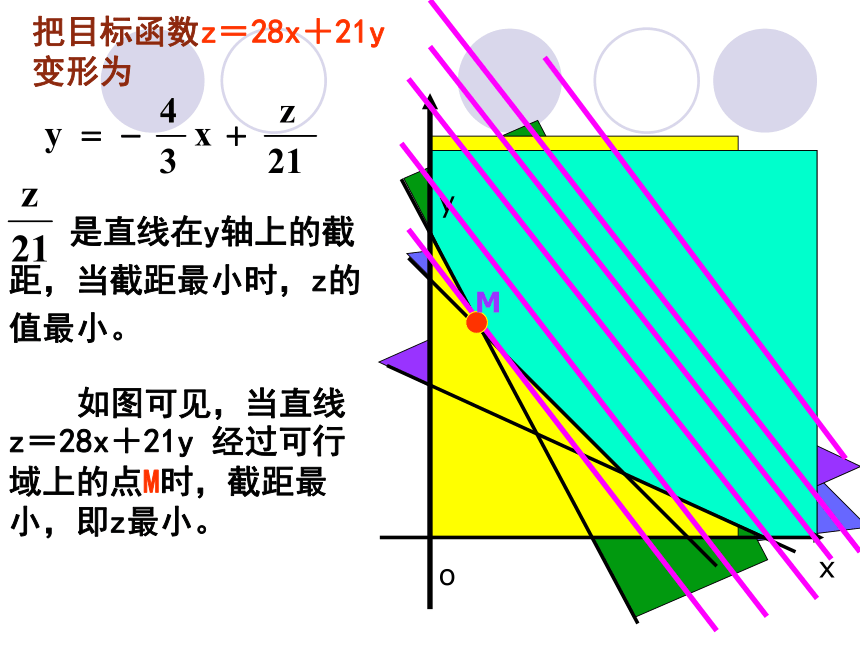
把目标函数z=28x+21y 变形为
x
y
o
是直线在y轴上的截距,当截距最小时,z的值最小。
M
如图可见,当直线z=28x+21y 经过可行域上的点M时,截距最小,即z最小。
M点是两条直线的交点,解方程组
得M坐标:
所以zmin=28x+21y=16
由此可知,每天食用食物A143g,食物B约571g,能够满足日常饮食要求,又使花费最低,最低成本为16元。
实际问题
线性规划问题
寻找约束条件
建立目标函数
列表
设立变量
转化
注意: 1.约束条件要写全;
2.作图、计算要准确;
3.解题格式要规范.
小结
例2、要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
规格类型
钢板类型 A规格 B规格 C规格
第一种钢板 2 1 1
第二种钢板 1 2 3
今需要A、B、C三种规格的成品分别为15、18、27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少?
x
0
y
2x+y=15
x+3y=27
x+2y=18
x+y =0
直线x+y=12经过的整点是B(3,9)和C(4,8),
它们是最优解.
B(3,9)
C(4,8)
A(18/5,39/5)
x+y=12
调整优值法
2
4
6
18
12
8
27
2
4
6
8
10
15
A(18/5,39/5)
经过可行域内的整点B(3,9)和C(4,8)时,Z=x+y=12
是最优解.
网格法
在可行域内打出网格线,
x
0
y
A(18/5,39/5)
1
2
1
2
18
27
15
9
7
8
B(3,9)
C(4,8)
整点问题解法
2、打网格线的方法(要求图精确)
1、调整优值法
3、周围找点检验
1、某工厂生产甲、乙两种产品.已知生产甲种产品1t需耗 A 种矿石10t,B种矿石5t,煤4t. 生产乙种产品1t需耗A种矿石4t, B种矿石4t, 煤9t. 每1t甲种产品的利润为600元,每1t乙种产品的利润是1000元. 工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t, B种矿石不超过200t, 煤不超过360t, 甲、乙两种产品各生产多少t (精确到0.1), 能使利润总额最大.
练习
依据题中已知条件,列表如下:
甲产品(1t) 乙产品(1t) 资源限制(t)
A种矿石(t) 10 4 300
B种矿石(t) 5 4 200
煤(t) 4 9 360
利润(元) 600 1000
[解] 设生产甲、乙两种产品分别为 xt、yt,利润总额为Z元,那么
作出以上不等式组所表示的平面区域,即可行域.
Z=600x+1000y
y
x
o
10
10
y
x
o
10
10
y
x
o
10
10
y
x
o
10
10
y
x
o
10
10
y
x
o
10
10
作直线l:600x+1000y=0,即直线l:3x+5y=0.
y
x
o
10
10
把直线l向右上方平移至l1的位置时,直线经过可行域上的点M,且与原点距离最大. 此时Z=600x+1000y取最大值.
y
x
o
10
10
解方程组:
2、某人有楼房一幢,室内面积共180m2,拟分隔成两类房间作为旅游客房,大房间每间面积为18m2,可住游客5名,每名游客每天住宿费为40元;小房间每间面积为15m2,可住游客3名,每名游客每天住宿费为50元;装修大房间每间需要1000元,装修小房间需要600元。如果他只能筹款8000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,能获得最大收益?
解:设大房间为x间,小房间为y间,则
且目标函数为Z=200x+150y
作业:教材P93 A3,A4,B3
《学法大视野 第30课时》
3.3.2简单的线性规划问题(二)
二元一次不等式 表示平面区域
直线定界, 特殊点定域
简单的线性规划
约束条件
目标函数
可行解
可行域
最优解
应用
求解方法:平移直线法、代点验算法
复习回顾
1. 求不等式|x-2|+|y-2|≤2所表示平面区域的面积。
2.在直角坐标系中,已知三角形AOB三边所在直线的方
程分别为x=0,y=0,2x+3y=30,则三角形AOB内部和
边上整点(横、纵坐标均为整数的点)的个数是( )
A.95 B.91 C.88 D.75
S=8
B
自主学习
3. x,y满足约束条件
(1)求Z=3x+5y的最大值和最小值
自主学习
3.解:作出可行域
x
y
o
A
B
C
直线经过A点时,Z取最大值;直线经过B点时,Z取最小值。
求得A(1.5,2.5),B(-2,-1),则Zmax=17,Zmin=-11。
例1、营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1千克食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?
食物/kg 碳水化合物/kg 蛋白质/kg 脂肪/kg
A 0.105 0.07 0.14
B 0.105 0.14 0.07
分析:将已知数据列成表格
合作学习
解:设每天食用xkg食物A,ykg食物B,总成本为z,
目标函数为:z=28x+21y
合作学习
食物/kg 碳水化合物/kg 蛋白质/kg 脂肪/kg
A 0.105 0.07 0.14
B 0.105 0.14 0.07
把目标函数z=28x+21y 变形为
x
y
o
是直线在y轴上的截距,当截距最小时,z的值最小。
M
如图可见,当直线z=28x+21y 经过可行域上的点M时,截距最小,即z最小。
M点是两条直线的交点,解方程组
得M坐标:
所以zmin=28x+21y=16
由此可知,每天食用食物A143g,食物B约571g,能够满足日常饮食要求,又使花费最低,最低成本为16元。
实际问题
线性规划问题
寻找约束条件
建立目标函数
列表
设立变量
转化
注意: 1.约束条件要写全;
2.作图、计算要准确;
3.解题格式要规范.
小结
例2、要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
规格类型
钢板类型 A规格 B规格 C规格
第一种钢板 2 1 1
第二种钢板 1 2 3
今需要A、B、C三种规格的成品分别为15、18、27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少?
x
0
y
2x+y=15
x+3y=27
x+2y=18
x+y =0
直线x+y=12经过的整点是B(3,9)和C(4,8),
它们是最优解.
B(3,9)
C(4,8)
A(18/5,39/5)
x+y=12
调整优值法
2
4
6
18
12
8
27
2
4
6
8
10
15
A(18/5,39/5)
经过可行域内的整点B(3,9)和C(4,8)时,Z=x+y=12
是最优解.
网格法
在可行域内打出网格线,
x
0
y
A(18/5,39/5)
1
2
1
2
18
27
15
9
7
8
B(3,9)
C(4,8)
整点问题解法
2、打网格线的方法(要求图精确)
1、调整优值法
3、周围找点检验
1、某工厂生产甲、乙两种产品.已知生产甲种产品1t需耗 A 种矿石10t,B种矿石5t,煤4t. 生产乙种产品1t需耗A种矿石4t, B种矿石4t, 煤9t. 每1t甲种产品的利润为600元,每1t乙种产品的利润是1000元. 工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t, B种矿石不超过200t, 煤不超过360t, 甲、乙两种产品各生产多少t (精确到0.1), 能使利润总额最大.
练习
依据题中已知条件,列表如下:
甲产品(1t) 乙产品(1t) 资源限制(t)
A种矿石(t) 10 4 300
B种矿石(t) 5 4 200
煤(t) 4 9 360
利润(元) 600 1000
[解] 设生产甲、乙两种产品分别为 xt、yt,利润总额为Z元,那么
作出以上不等式组所表示的平面区域,即可行域.
Z=600x+1000y
y
x
o
10
10
y
x
o
10
10
y
x
o
10
10
y
x
o
10
10
y
x
o
10
10
y
x
o
10
10
作直线l:600x+1000y=0,即直线l:3x+5y=0.
y
x
o
10
10
把直线l向右上方平移至l1的位置时,直线经过可行域上的点M,且与原点距离最大. 此时Z=600x+1000y取最大值.
y
x
o
10
10
解方程组:
2、某人有楼房一幢,室内面积共180m2,拟分隔成两类房间作为旅游客房,大房间每间面积为18m2,可住游客5名,每名游客每天住宿费为40元;小房间每间面积为15m2,可住游客3名,每名游客每天住宿费为50元;装修大房间每间需要1000元,装修小房间需要600元。如果他只能筹款8000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,能获得最大收益?
解:设大房间为x间,小房间为y间,则
且目标函数为Z=200x+150y
作业:教材P93 A3,A4,B3
《学法大视野 第30课时》
