人教版数学 八年级下册 18.1 平行四边形 培优训练(含答案)
文档属性
| 名称 | 人教版数学 八年级下册 18.1 平行四边形 培优训练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 373.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 07:00:31 | ||
图片预览

文档简介
人教版
八年级下册
18.1
平行四边形
培优训练(含答案)
一、选择题(本大题共6道小题)
1.
以三角形的三个顶点作平行四边形,最多可以作(
)
A.2个
B.3个
C.4个
D.5个
2.
点、、、在同一平面内,从①,②,③,④.这四个条件中任选两个,能使四边形是平行四边形的选法有(
)种
A.
B.
C.
D.
3.
在平行四边形中,点、、、和、、、分别为和的五等分点,点、和、分别是和的三等分点,已知四边形的面积为,则平行四边形面积为(
)
A.2
B.
C.
D.
4.
如图,在平行四边中,、为对角线,,边上的高为,则阴影部分的面积为(
).
A.3
B.6
C.12
D.24
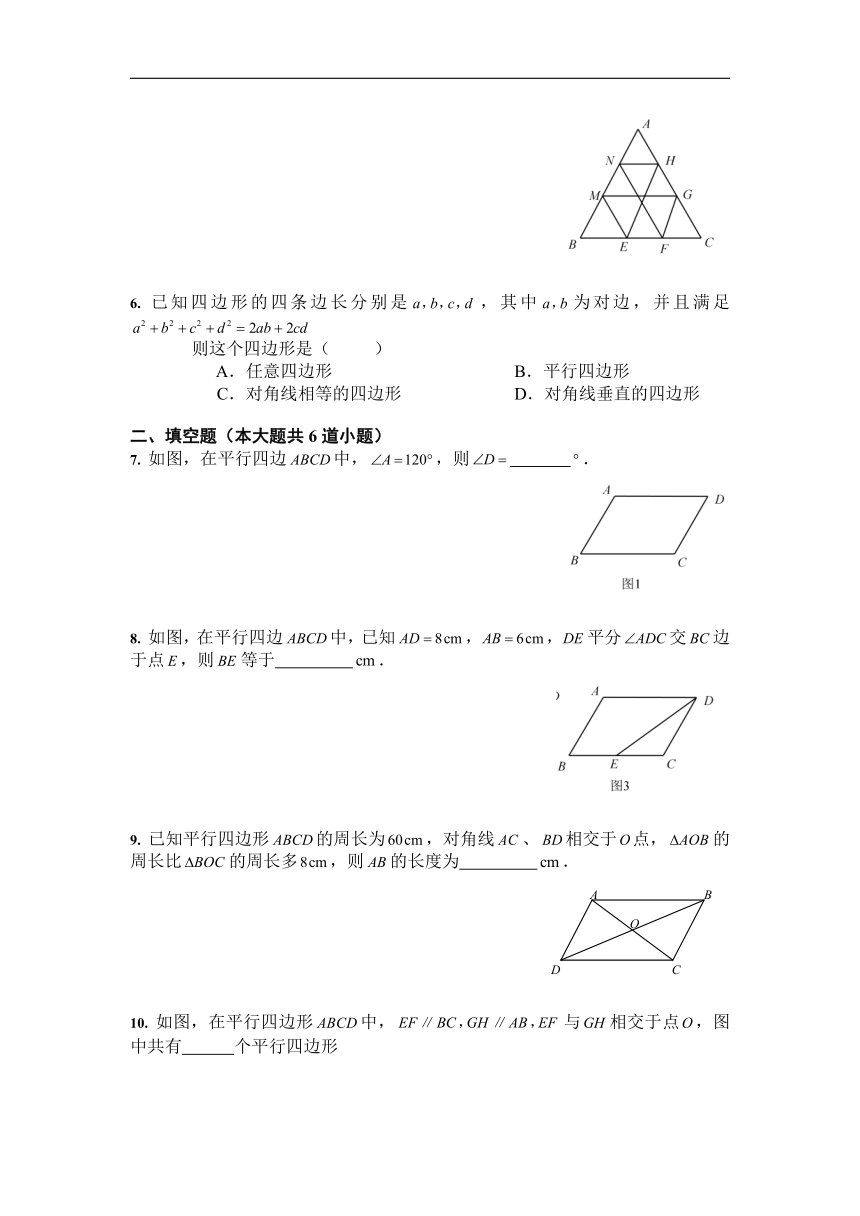
5.
如图,点分别在的边上,且
,,有黑、白两只蚂蚁,它们同时同速从点出发,黑蚂蚁沿路线爬行,白蚂蚁沿路线爬行,那么(
)
黑蚂蚁先回到点
白蚂蚁先回到点
两只蚂蚁同时回到点
哪只蚂蚁先回到点视各点的位置而定
6.
已知四边形的四条边长分别是,其中为对边,并且满足
则这个四边形是(
)
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形
二、填空题(本大题共6道小题)
7.
如图,在平行四边中,,则
.
8.
如图,在平行四边中,已知,,平分交边于点,则等于
.
9.
已知平行四边形的周长为,对角线、相交于点,的周长比的周长多,则的长度为
.
10.
如图,在平行四边形中,与相交于点,图中共有
个平行四边形
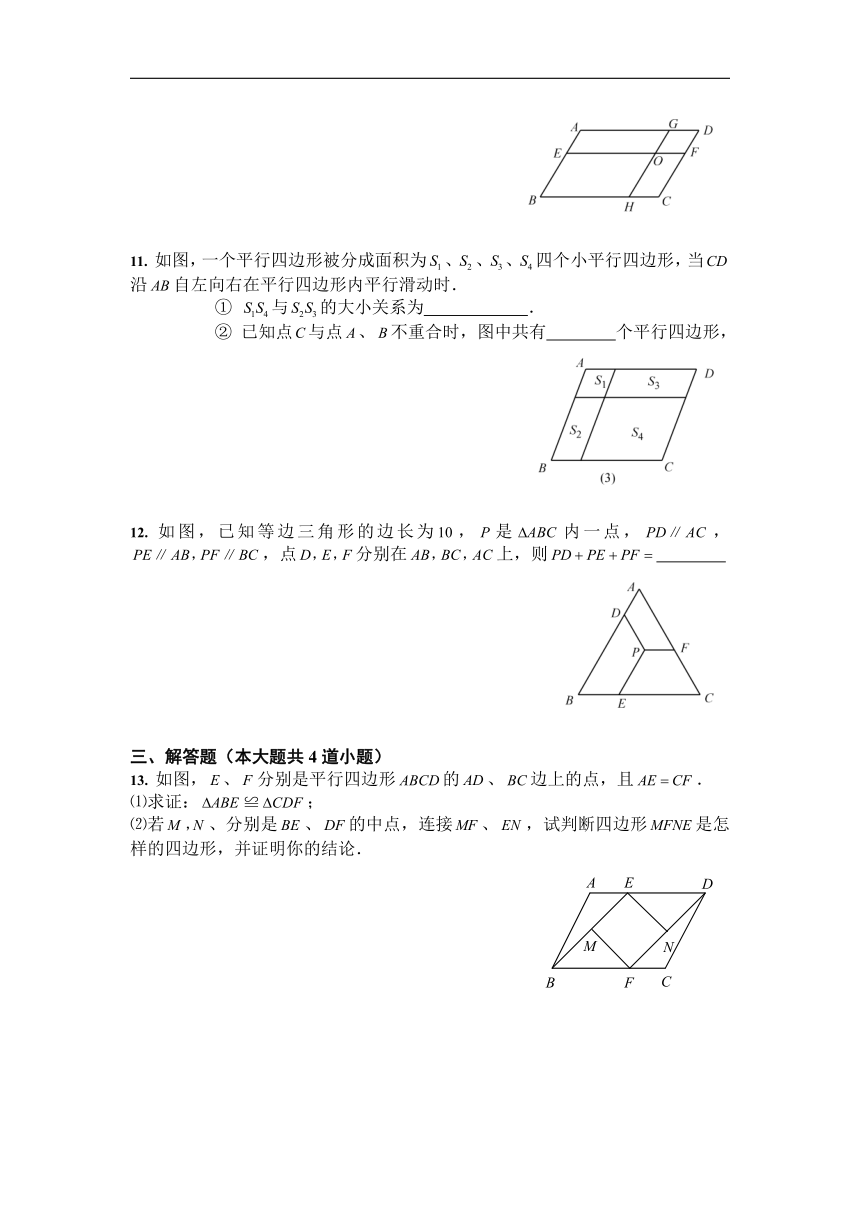
11.
如图,一个平行四边形被分成面积为、、、四个小平行四边形,当沿自左向右在平行四边形内平行滑动时.
①
与的大小关系为
.
②
已知点与点、不重合时,图中共有
个平行四边形,
12.
如图,已知等边三角形的边长为,是内一点,,,点分别在上,则
三、解答题(本大题共4道小题)
13.
如图,、分别是平行四边形的、边上的点,且.
⑴求证:≌;
⑵若、分别是、的中点,连接、,试判断四边形是怎样的四边形,并证明你的结论.
14.
已知:如图,平行四边形内有一点满足于点,,,请找出与相等的一条线段,并给予证明.
15.
如图,在等腰中,延长边到点,延长边到点,连接,恰有.求证:.
16.
如图所示,在平行四边形中,求证.
人教版
八年级下册
18.1
平行四边形
培优训练-答案
一、选择题(本大题共6道小题)
1.
【答案】B
2.
【答案】B
3.
【答案】C
4.
【答案】C
5.
【答案】C
【解析】可知四边形均为平行四边形,可知选C
6.
【答案】B
二、填空题(本大题共6道小题)
7.
【答案】
8.
【答案】
【解析】∵,,∴.
9.
【答案】
【解析】如图,的周长为,的周长为
由平行四边形的对角线互相平分可得
∴.
10.
【答案】个
11.
【答案】①;②
12.
【答案】
三、解答题(本大题共4道小题)
13.
【答案】
⑴由是平行四边形可知,,
又,故≌
⑵由(1)可知,,
又,,∴
而∥,∴有
∴,∴∥
∴四边形为平行四边形
14.
【答案】
或.
证明:延长交于,
∵且
∴
又∵
∴为等腰直角三角形
∴
在和中
∴
∴
15.
【答案】
由,知是等腰三角形,其底角必为钝角,所以等腰中,必为钝角,因此必为等腰的顶角,则、是腰,即.
过作的平行线,与过所作的平行线交于点,则四边形为平行四边形,故,,.
从而,.
连,在和中,
,,
,
则,于是.
而,即知是等边三角形,从而
.
设,则
,
,
.
由,得
.解得,即.
16.
【答案】
本题实质是证明.
如图所示,过点作交的延长线于点,
因为,,
故是平行四边形,从而,.
作,是垂足,则:
,
,
故.
八年级下册
18.1
平行四边形
培优训练(含答案)
一、选择题(本大题共6道小题)
1.
以三角形的三个顶点作平行四边形,最多可以作(
)
A.2个
B.3个
C.4个
D.5个
2.
点、、、在同一平面内,从①,②,③,④.这四个条件中任选两个,能使四边形是平行四边形的选法有(
)种
A.
B.
C.
D.
3.
在平行四边形中,点、、、和、、、分别为和的五等分点,点、和、分别是和的三等分点,已知四边形的面积为,则平行四边形面积为(
)
A.2
B.
C.
D.
4.
如图,在平行四边中,、为对角线,,边上的高为,则阴影部分的面积为(
).
A.3
B.6
C.12
D.24
5.
如图,点分别在的边上,且
,,有黑、白两只蚂蚁,它们同时同速从点出发,黑蚂蚁沿路线爬行,白蚂蚁沿路线爬行,那么(
)
黑蚂蚁先回到点
白蚂蚁先回到点
两只蚂蚁同时回到点
哪只蚂蚁先回到点视各点的位置而定
6.
已知四边形的四条边长分别是,其中为对边,并且满足
则这个四边形是(
)
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形
二、填空题(本大题共6道小题)
7.
如图,在平行四边中,,则
.
8.
如图,在平行四边中,已知,,平分交边于点,则等于
.
9.
已知平行四边形的周长为,对角线、相交于点,的周长比的周长多,则的长度为
.
10.
如图,在平行四边形中,与相交于点,图中共有
个平行四边形
11.
如图,一个平行四边形被分成面积为、、、四个小平行四边形,当沿自左向右在平行四边形内平行滑动时.
①
与的大小关系为
.
②
已知点与点、不重合时,图中共有
个平行四边形,
12.
如图,已知等边三角形的边长为,是内一点,,,点分别在上,则
三、解答题(本大题共4道小题)
13.
如图,、分别是平行四边形的、边上的点,且.
⑴求证:≌;
⑵若、分别是、的中点,连接、,试判断四边形是怎样的四边形,并证明你的结论.
14.
已知:如图,平行四边形内有一点满足于点,,,请找出与相等的一条线段,并给予证明.
15.
如图,在等腰中,延长边到点,延长边到点,连接,恰有.求证:.
16.
如图所示,在平行四边形中,求证.
人教版
八年级下册
18.1
平行四边形
培优训练-答案
一、选择题(本大题共6道小题)
1.
【答案】B
2.
【答案】B
3.
【答案】C
4.
【答案】C
5.
【答案】C
【解析】可知四边形均为平行四边形,可知选C
6.
【答案】B
二、填空题(本大题共6道小题)
7.
【答案】
8.
【答案】
【解析】∵,,∴.
9.
【答案】
【解析】如图,的周长为,的周长为
由平行四边形的对角线互相平分可得
∴.
10.
【答案】个
11.
【答案】①;②
12.
【答案】
三、解答题(本大题共4道小题)
13.
【答案】
⑴由是平行四边形可知,,
又,故≌
⑵由(1)可知,,
又,,∴
而∥,∴有
∴,∴∥
∴四边形为平行四边形
14.
【答案】
或.
证明:延长交于,
∵且
∴
又∵
∴为等腰直角三角形
∴
在和中
∴
∴
15.
【答案】
由,知是等腰三角形,其底角必为钝角,所以等腰中,必为钝角,因此必为等腰的顶角,则、是腰,即.
过作的平行线,与过所作的平行线交于点,则四边形为平行四边形,故,,.
从而,.
连,在和中,
,,
,
则,于是.
而,即知是等边三角形,从而
.
设,则
,
,
.
由,得
.解得,即.
16.
【答案】
本题实质是证明.
如图所示,过点作交的延长线于点,
因为,,
故是平行四边形,从而,.
作,是垂足,则:
,
,
故.
