完全平方公式
图片预览





文档简介
(共16张PPT)
我们学过一个什么公式?(关于平方的)
有没有同学愿意和和我们大家分享一下
(叙述平方差公式的内容并用字母表示)
想一想:
平方差公式
(a+b)(a-b)=a2+b2
两个数的和与这两个数的差的积等于这两个数的平方差
怎样得到的呢?
(a+b)(a-b) =a2+ab-ab-b2= a2 -b2
说一说:
①103×97
②103 × 103
解: 103×97
=(100+3)(100-3)
= 1002 -32
= 10000 -9
= 9991
请同学们自编一个符合平方差公式结构的计算题,计算并说一说自己所编的题。
解: 103 × 103
=(100+3)(100 +3)
=1002 +100×3 +3×100 + 32
=10000 +300 +300 +9
=10609
(a+b)2
(a-b)2
分析:我们可以用多项式乘多项式的方法计算
(a+b)2=(a+b)(a+b)、(a-b)2=(a-b)(a-b)
(要求独立思考完成)
请下面完成的同学看看我们在黑板上做的同学和你的一不一样?不一样的同学说一说你的看法?
可以得到这样两个公式:
可合并为:
两数和(或差)的平方,等于它们的平方和,
加上(或减去)它们的积的2倍。
和
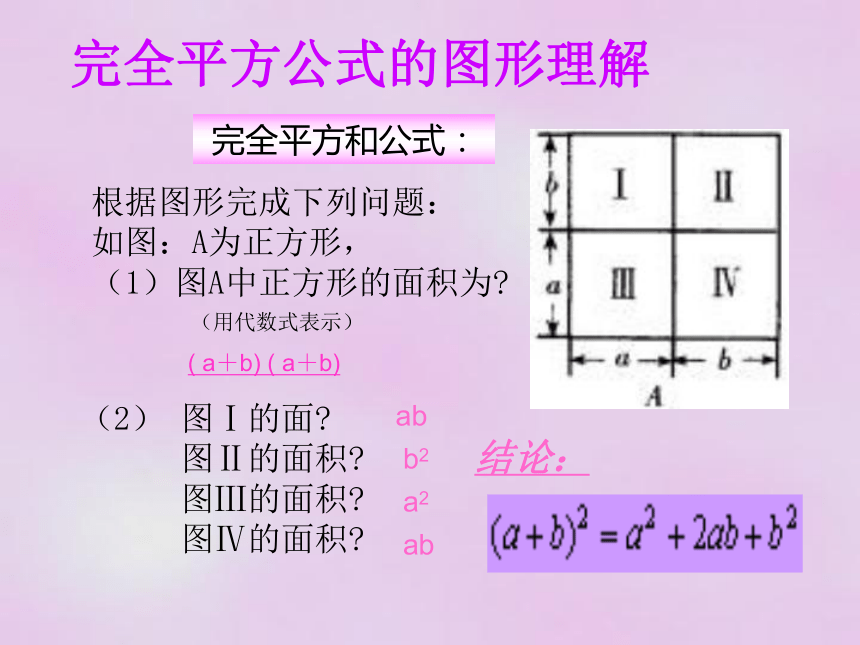
完全平方公式的图形理解
根据图形完成下列问题:
如图:A为正方形,
(1)图A中正方形的面积为
(用代数式表示)
完全平方和公式:
(2) 图Ⅰ的面
图Ⅱ的面积
图Ⅲ的面积
图Ⅳ的面积
( a+b) ( a+b)
ab
b2
a2
ab
结论:
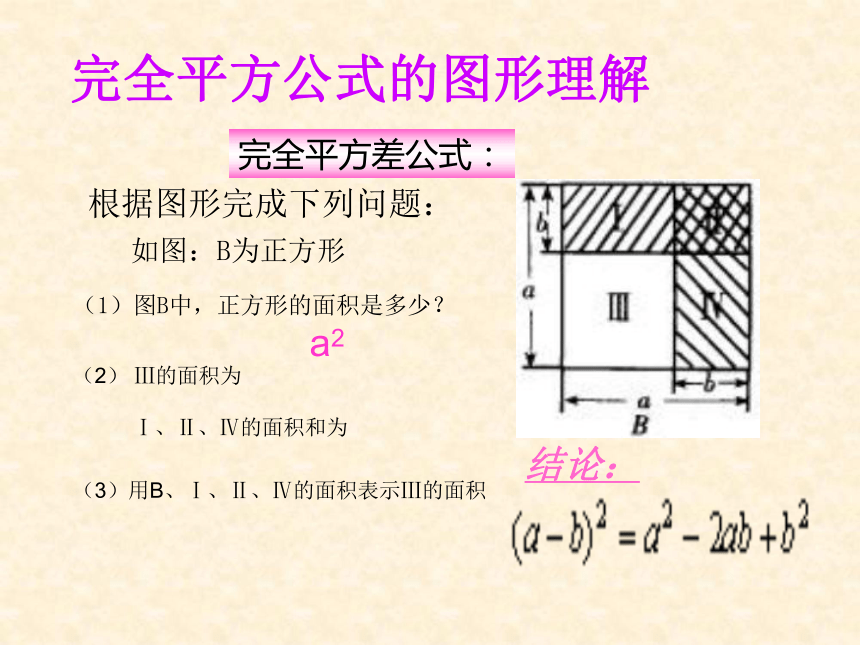
(1)图B中,正方形的面积是多少?
完全平方公式的图形理解
完全平方差公式:
根据图形完成下列问题:
如图:B为正方形
a2
(2) Ⅲ的面积为
Ⅰ、Ⅱ、Ⅳ的面积和为
(3)用B、Ⅰ、Ⅱ、Ⅳ的面积表示Ⅲ的面积
结论:
2
一、利用完全平方公式计算:
分析:
在
2
中,把x看成a,把2y看成b,
则:就可用完全平方公式来计算,即
(1)
2
2
2
2
2
2
2
2
中把2x看成a,把3y看成b,
一、利用完全平方公式计算:
(2)
分析:
在
则:就可用完全平方公式来计算,即
2
2
2
2
2
2
二、利用完全平方公式计算:
2
2
2
(1)
(2)
(3)
运用完全平方公式计算:
(1)
(3)
(4)
(5)
(6)
(7)
(8)
(2)
1、运用完全平方公式计算:
(1)
(2)
(3)
(4)
102=100+2
199=200-1
79.8=80 - 0.2
498=500-2
2、运用乘法公式计算:
(1)
(2)
(3)
(4)
1、完全平方公式:
2、注意:项数、符号、字母及其指数;
4、解题时常用结论:
(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2
3、字母指数:当公式中的a、b所代表
的单项式字母指数不是1时,乘方时
要记住字母指数需乘2。
P 133 1,2、(3)(4).
我们学过一个什么公式?(关于平方的)
有没有同学愿意和和我们大家分享一下
(叙述平方差公式的内容并用字母表示)
想一想:
平方差公式
(a+b)(a-b)=a2+b2
两个数的和与这两个数的差的积等于这两个数的平方差
怎样得到的呢?
(a+b)(a-b) =a2+ab-ab-b2= a2 -b2
说一说:
①103×97
②103 × 103
解: 103×97
=(100+3)(100-3)
= 1002 -32
= 10000 -9
= 9991
请同学们自编一个符合平方差公式结构的计算题,计算并说一说自己所编的题。
解: 103 × 103
=(100+3)(100 +3)
=1002 +100×3 +3×100 + 32
=10000 +300 +300 +9
=10609
(a+b)2
(a-b)2
分析:我们可以用多项式乘多项式的方法计算
(a+b)2=(a+b)(a+b)、(a-b)2=(a-b)(a-b)
(要求独立思考完成)
请下面完成的同学看看我们在黑板上做的同学和你的一不一样?不一样的同学说一说你的看法?
可以得到这样两个公式:
可合并为:
两数和(或差)的平方,等于它们的平方和,
加上(或减去)它们的积的2倍。
和
完全平方公式的图形理解
根据图形完成下列问题:
如图:A为正方形,
(1)图A中正方形的面积为
(用代数式表示)
完全平方和公式:
(2) 图Ⅰ的面
图Ⅱ的面积
图Ⅲ的面积
图Ⅳ的面积
( a+b) ( a+b)
ab
b2
a2
ab
结论:
(1)图B中,正方形的面积是多少?
完全平方公式的图形理解
完全平方差公式:
根据图形完成下列问题:
如图:B为正方形
a2
(2) Ⅲ的面积为
Ⅰ、Ⅱ、Ⅳ的面积和为
(3)用B、Ⅰ、Ⅱ、Ⅳ的面积表示Ⅲ的面积
结论:
2
一、利用完全平方公式计算:
分析:
在
2
中,把x看成a,把2y看成b,
则:就可用完全平方公式来计算,即
(1)
2
2
2
2
2
2
2
2
中把2x看成a,把3y看成b,
一、利用完全平方公式计算:
(2)
分析:
在
则:就可用完全平方公式来计算,即
2
2
2
2
2
2
二、利用完全平方公式计算:
2
2
2
(1)
(2)
(3)
运用完全平方公式计算:
(1)
(3)
(4)
(5)
(6)
(7)
(8)
(2)
1、运用完全平方公式计算:
(1)
(2)
(3)
(4)
102=100+2
199=200-1
79.8=80 - 0.2
498=500-2
2、运用乘法公式计算:
(1)
(2)
(3)
(4)
1、完全平方公式:
2、注意:项数、符号、字母及其指数;
4、解题时常用结论:
(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2
3、字母指数:当公式中的a、b所代表
的单项式字母指数不是1时,乘方时
要记住字母指数需乘2。
P 133 1,2、(3)(4).
