19.1.1 平行四边形的性质(1)(含答案)
文档属性
| 名称 | 19.1.1 平行四边形的性质(1)(含答案) |

|
|
| 格式 | rar | ||
| 文件大小 | 34.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-19 18:59:51 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
19.1.1 平行四边形的性质(1)
◆回顾归纳
1.两组对边_______的四边形叫做平行四边形.
2.平行四边形的对边______,对角________.
◆课堂测控
测试点 平行四边形的边角性质
1.在ABCD中:(1)若∠A=100°,则∠B=_____,∠C=____,∠D=_____.
(2)若AB=2,AD=5,则BC=_____,CD=_____,ABCD的周长等于______.
2.已知平行四边形的邻边的比是3:5,它的周长是48cm,则该平行四边形的一组邻边长分别为_____cm和_____cm.
3.如图1所示,ABCD中,E,G是AD上的两点,F,H是BC上的两点,且AB∥EF∥GH∥DC.则图中的平行四边形共有_____个.
图1 图2 图3
◆课后测控
1.在ABCD中,AB+BC=10,则ABCD的周长是______.
2.在四边形ABCD中,AB∥DC,AD∥BC,若∠B=70°,那么∠D=_____,∠C=_____.
3.ABCD中,两个邻边的比为3:2,其中较长的一边为15cm,则ABCD的周长为____.
4.ABCD中,∠A的补角和∠C的补角的和是210°,则∠A=_____,∠B=_____.
5.如图2所示,四边形ABCD,ABDE都是平行四边形,且ABCD的面积是4cm2,那么四边形ABCE的面积是_____cm2.
6.从平行四边形的一个锐角顶点向对边作两条高线,如果这两条高线的夹角为135°,则这个平行四边形的各内角度数为_______.
7.如图3所示,ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( )
A.18° B.36° C.72° D.108°
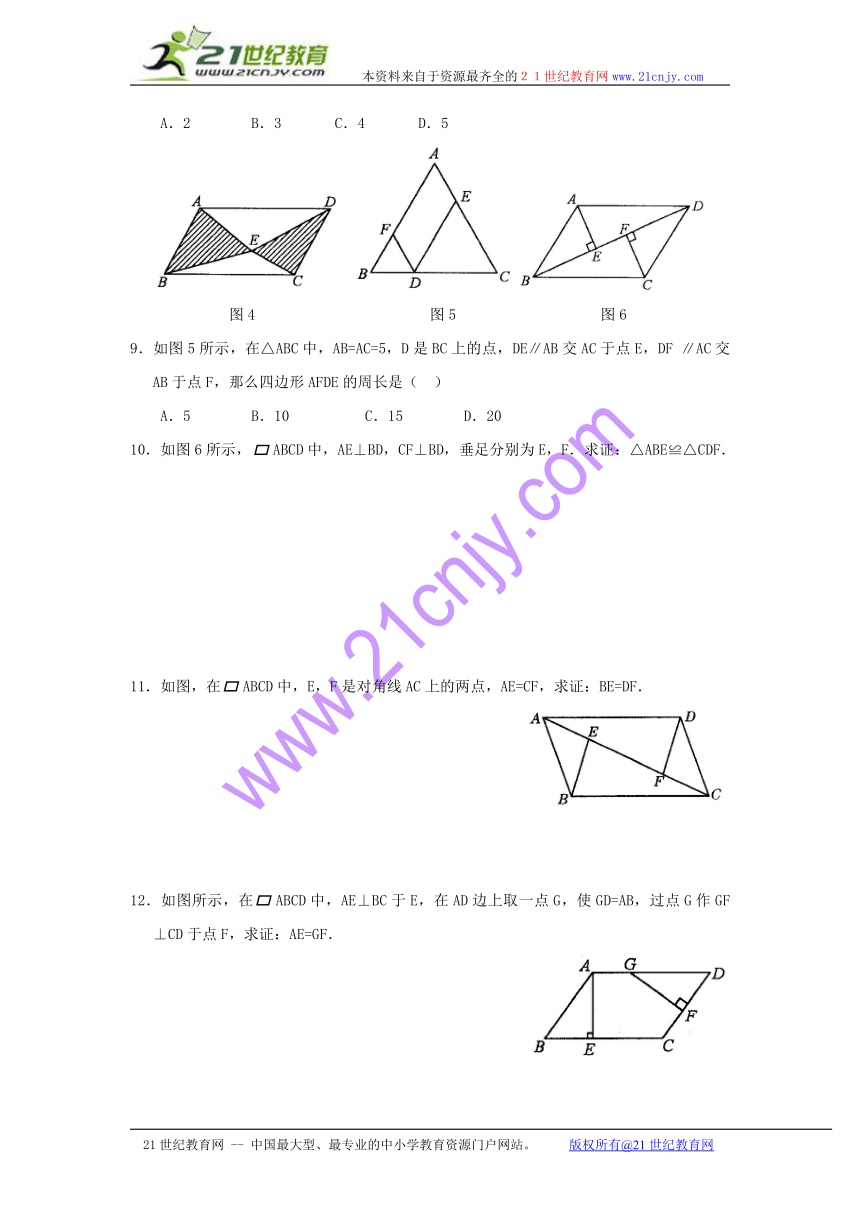
8.如图4所示,E是ABCD内任一点,若S四边形ABCD=6,则图中阴影部分的面积为( )
A.2 B.3 C.4 D.5
( http: / / )
图4 图5 图6
9.如图5所示,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( )
A.5 B.10 C.15 D.20
10.如图6所示,ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ABE≌△CDF.
11.如图,在ABCD中,E,F是对角线AC上的两点,AE=CF,求证:BE=DF.
12.如图所示,在ABCD中,AE⊥BC于E,在AD边上取一点G,使GD=AB,过点G作GF⊥CD于点F,求证:AE=GF.
( http: / / )
◆拓展创新
13.如图所示是某城市部分街道,AF∥BC,EC⊥BC,BA∥DE,BD∥AE,甲,乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F;乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误的时间相同,那么谁先到达F站?请说明理由.
答案:
回顾归纳
1.分别平行 2.相等,相等
课堂测控
1.(1)80°,100°,80° (2)5,2,14
2.9,15 3.6
课后测控
1.20 2.70°,110° 3.50cm
4.75°,105° 点拨:∠A=∠C.
5.6 6.45°,45°,135°,135° 7.B
8.B 点拨:图中阴影部分面积等于平行四边形面积的一半.
9.B 点拨:AFDE的周长等于AB+AC.
10.∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB.
又∵AE⊥BD,CF⊥BD,∴△ABE≌△CDF.
11.∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF.
又∵AE=CF,∴△ABE≌△CDF.
∴BE=DF.
12.点拨:证△ABE≌△GDF.
拓展创新
13.甲和乙同时到达,理由如下:
∵BA∥DE,BD∥AE,
∴四边形ABDE为平行四边形.
∴AB=DE,AE=BD.
又∵AB=CD,∴DE=DC,
∵AF∥BC,EC⊥BC,
∴在等腰△EDC中,∠EFD=∠ECB=90°.
∴CF=EF.
∴AB+AE+EF=BD+DC+CF.
因为两车速度相同,途中耽误时间相同,故甲和乙两人同时到达.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
19.1.1 平行四边形的性质(1)
◆回顾归纳
1.两组对边_______的四边形叫做平行四边形.
2.平行四边形的对边______,对角________.
◆课堂测控
测试点 平行四边形的边角性质
1.在ABCD中:(1)若∠A=100°,则∠B=_____,∠C=____,∠D=_____.
(2)若AB=2,AD=5,则BC=_____,CD=_____,ABCD的周长等于______.
2.已知平行四边形的邻边的比是3:5,它的周长是48cm,则该平行四边形的一组邻边长分别为_____cm和_____cm.
3.如图1所示,ABCD中,E,G是AD上的两点,F,H是BC上的两点,且AB∥EF∥GH∥DC.则图中的平行四边形共有_____个.
图1 图2 图3
◆课后测控
1.在ABCD中,AB+BC=10,则ABCD的周长是______.
2.在四边形ABCD中,AB∥DC,AD∥BC,若∠B=70°,那么∠D=_____,∠C=_____.
3.ABCD中,两个邻边的比为3:2,其中较长的一边为15cm,则ABCD的周长为____.
4.ABCD中,∠A的补角和∠C的补角的和是210°,则∠A=_____,∠B=_____.
5.如图2所示,四边形ABCD,ABDE都是平行四边形,且ABCD的面积是4cm2,那么四边形ABCE的面积是_____cm2.
6.从平行四边形的一个锐角顶点向对边作两条高线,如果这两条高线的夹角为135°,则这个平行四边形的各内角度数为_______.
7.如图3所示,ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( )
A.18° B.36° C.72° D.108°
8.如图4所示,E是ABCD内任一点,若S四边形ABCD=6,则图中阴影部分的面积为( )
A.2 B.3 C.4 D.5
( http: / / )
图4 图5 图6
9.如图5所示,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( )
A.5 B.10 C.15 D.20
10.如图6所示,ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ABE≌△CDF.
11.如图,在ABCD中,E,F是对角线AC上的两点,AE=CF,求证:BE=DF.
12.如图所示,在ABCD中,AE⊥BC于E,在AD边上取一点G,使GD=AB,过点G作GF⊥CD于点F,求证:AE=GF.
( http: / / )
◆拓展创新
13.如图所示是某城市部分街道,AF∥BC,EC⊥BC,BA∥DE,BD∥AE,甲,乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F;乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误的时间相同,那么谁先到达F站?请说明理由.
答案:
回顾归纳
1.分别平行 2.相等,相等
课堂测控
1.(1)80°,100°,80° (2)5,2,14
2.9,15 3.6
课后测控
1.20 2.70°,110° 3.50cm
4.75°,105° 点拨:∠A=∠C.
5.6 6.45°,45°,135°,135° 7.B
8.B 点拨:图中阴影部分面积等于平行四边形面积的一半.
9.B 点拨:AFDE的周长等于AB+AC.
10.∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB.
又∵AE⊥BD,CF⊥BD,∴△ABE≌△CDF.
11.∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF.
又∵AE=CF,∴△ABE≌△CDF.
∴BE=DF.
12.点拨:证△ABE≌△GDF.
拓展创新
13.甲和乙同时到达,理由如下:
∵BA∥DE,BD∥AE,
∴四边形ABDE为平行四边形.
∴AB=DE,AE=BD.
又∵AB=CD,∴DE=DC,
∵AF∥BC,EC⊥BC,
∴在等腰△EDC中,∠EFD=∠ECB=90°.
∴CF=EF.
∴AB+AE+EF=BD+DC+CF.
因为两车速度相同,途中耽误时间相同,故甲和乙两人同时到达.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
