陕西省吴起高中2019-2020学年高二下学期第三次质量检测数学(理)试题 Word版含答案
文档属性
| 名称 | 陕西省吴起高中2019-2020学年高二下学期第三次质量检测数学(理)试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 327.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 03:59:15 | ||
图片预览



文档简介
____________________________________________________________________________________________
吴起高中2019—2020学年第二学期
高二第三次质量检测理科数学试题
(全卷150分
时间120分钟)
第I卷(选择题共60分)
一、单选题(本题共60分,每小题5分,每个小题只有一个正确选项)
1.已知复数(虚数单位),则的虚部为(
)
A.
B.
C.
D.
2.参数方程(为参数)化为普通方程为(
)
A.
B.
C.
D.
3.命题“对于任意角
,”的证明:“”,
其过程应用了(
)
A.分析法
B.综合法
C.综合法、分析法综合使用
D.间接证法
4.某高校外语系有8名志愿者,其中有5名男生,3名女生,现从中选3人参加某项测试赛的翻译工作,若要求这3人中既有男生,又有女生,则不同的选法共有(
)
A.120种
B.90种
C.56种
D.45种
5.已知随机变量,若,则,分别是(
)
A.6和2.4
B.2和2.4
C.4和2.4
D.4和5.6
6.已知三角形的三边长分别为,,,内切圆的半径为;则三角形的面积为;四面体的四个面的面积分别为,内切球的半径为.类比三角形的面积可得四面体的体积为
(
)
A.
B.
C.
D.
7.一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X是一个随机变量,其分布列为P(X
),则P(X=4)的值为(
)
A.
B.
C.
D.
8.已知向量.若,则x的值为(
)
A.
B.2
C.3
D.
9.100件产品中有6件次品,现从中不放回的任取3件产品,在前两次抽到正品的条件下第三次抽到次品的概率为(
)
A.
B.
C.
D.
10.一个向量在基底下的坐标为,则在基底下的坐标为(
)
A.
B.
C.
D.
11.设,那么等于(
)
A.
B.
C.
D.
12.中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“数”必须排在前三节,且“射”和“御”两门课程相邻排课,则“六艺”课程讲座不同排课顺序共有(
)
A.种
B.种
C.种
D.种
第II卷(非选择题共90分)
二、填空题(本题共20分,每题5分)
13.已知复数,则___________;
14.二项式(1﹣2x)10展开式中,第5项的二项式系数为
.
15.某一智力游戏玩一次所得的积分是一个随机变量,其概率分布如表,数学期望.则
__________.
0
3
6
16.如图,一个地区分为5个行政区域,现给该地区的地图涂色,要求相邻区域不得使用同一种颜色,现有4种颜色可供选择,则涂色方法共有
种.
三、解答题(本题共70分,17题10分,18-22每小题12分)
17.如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
18.有11个划船运动员,其中右舷手4人,左舷手5人,还有甲、乙二人左、右都能划,现要选8人组成一个划船队参加竞赛(左、右各4人),有多少种安排方法?
19.在直角坐标系中,直线,圆,以坐标原点为极点,轴正半轴为极轴建立极坐标系.
(1)求,的极坐标方程;
(2)若直线的极坐标方程为,设的交点为,求的面积.
20.有6本不同的书,在下列不同的条件下,各有多少种不同的分法?
(1)分给甲、乙、丙三人,其中一个人1本,一个人2本,一个人3本;
(2)分成三组,一组4本,另外两组各1本;
(3)甲得1本,乙得1本,丙得4本.
21.在直角坐标系中,曲线过点,其参数方程为(为参数,),以为极点,轴非负半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)求曲线的普通方程和曲线的直角坐标方程;
(2)求已知曲线和曲线交于两点,且,求实数的值.
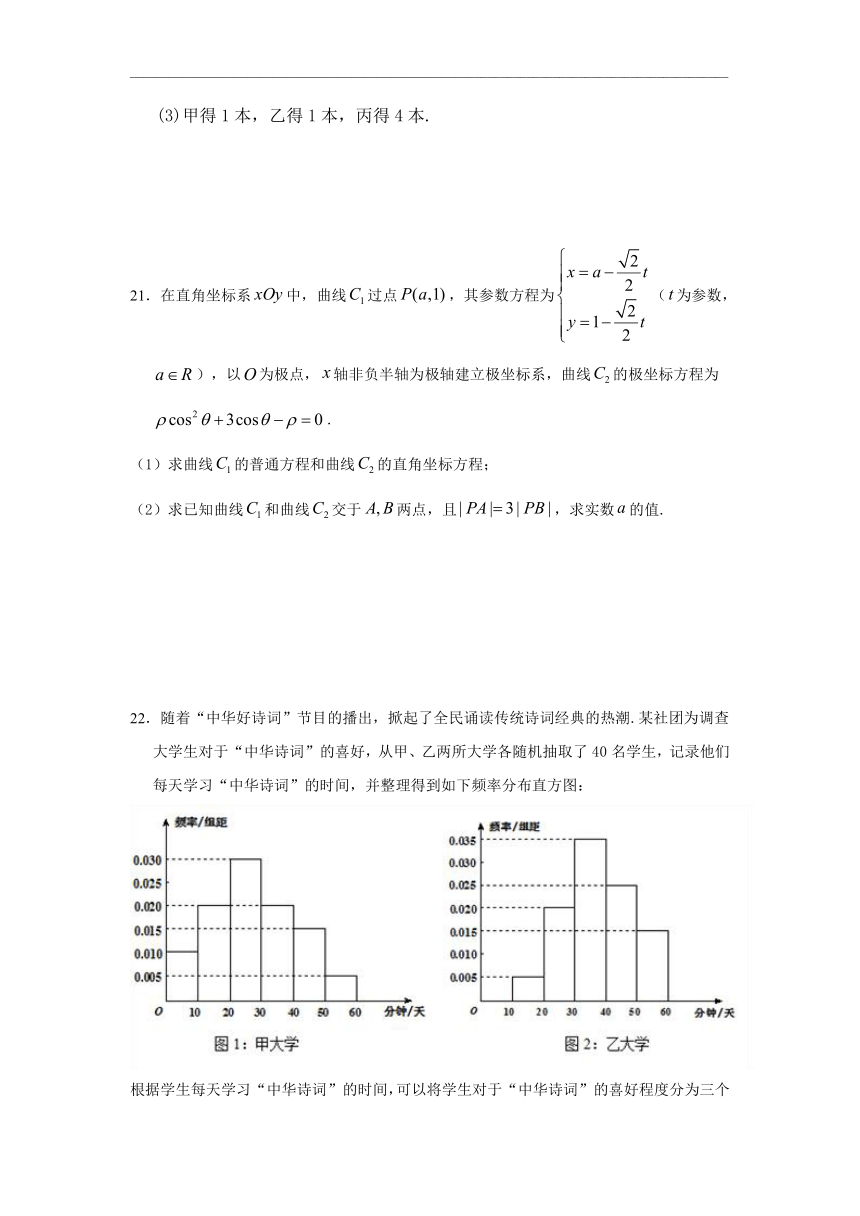
22.随着“中华好诗词”节目的播出,掀起了全民诵读传统诗词经典的热潮.某社团为调查大学生对于“中华诗词”的喜好,从甲、乙两所大学各随机抽取了40名学生,记录他们每天学习“中华诗词”的时间,并整理得到如下频率分布直方图:
根据学生每天学习“中华诗词”的时间,可以将学生对于“中华诗词”的喜好程度分为三个等级
:
(Ⅰ)从甲大学中随机选出一名学生,试估计其“爱好”中华诗词的概率;
(Ⅱ)从两组“痴迷”的同学中随机选出2人,记为选出的两人中甲大学的人数,求的分布列和数学期望;
(Ⅲ)试判断选出的这两组学生每天学习“中华诗词”时间的平均值与的大小,及方差与的大小.(只需写出结论)
吴起高中2019-2020学年第二学期高二第三次月考
理科数学(卷)参考答案
一、单选题(本题共60分,每小题5分,每个小题只有一个正确选项)
1-6
BABDCC
7-12DADBCA
二、填空题(本题共20分,每题5分)
13、
14、210
15、
16、72
三、解答题(本题共70分,17题10分,18-22每小题12分)
17证明(1)因为是长方体,所以侧面,而平面,所以
又,,平面,因此平面;
(2)以点坐标原点,以分别为轴,建立如下图所示的空间直角坐标系,
,
因为,所以,
所以,,
设是平面的法向量,
所以,
设是平面的法向量,
所以,
二面角的余弦值的绝对值为,
所以二面角的正弦值为.
18、解:按照右舷手为标准进行分类,分三类:
第一类:右舷手4人都入选有
第二类:右舷手3人入选;则从甲乙中选一人作右舷手有
第三类:右舷手2人入选,有
所以共有
19、(1)因为,所以的极坐标方程为,
的极坐标方程为
(2)将代入
得得,
所以
因为的半径为1,则的面积为
20、解:
21、
解:(1)的参数方程,消参得普通方程为,
的极坐标方程化为即;
(2)将曲线的参数方程标准化为(为参数,)
代入曲线得,由,
得
设,对应的参数为,,由题意得即或,
当时,,解得
,
当时,解得,
综上:或.
22、(Ⅰ)
由图知,甲大学随机选取的40名学生中,“爱好”中华诗词的频率为,
所以从甲大学中随机选出一名学生,“爱好”中华诗词的概率为.
(Ⅱ)
甲大学随机选取的40名学生中“痴迷”的学生有人,
乙大学随机选取的40名学生中“痴迷”的学生有人,
所以,随机变量的取值为.
所以,
,
,
.
所以的分布列为
0
1
2
P
的数学期望为
.
(Ⅲ)
;
吴起高中2019—2020学年第二学期
高二第三次质量检测理科数学试题
(全卷150分
时间120分钟)
第I卷(选择题共60分)
一、单选题(本题共60分,每小题5分,每个小题只有一个正确选项)
1.已知复数(虚数单位),则的虚部为(
)
A.
B.
C.
D.
2.参数方程(为参数)化为普通方程为(
)
A.
B.
C.
D.
3.命题“对于任意角
,”的证明:“”,
其过程应用了(
)
A.分析法
B.综合法
C.综合法、分析法综合使用
D.间接证法
4.某高校外语系有8名志愿者,其中有5名男生,3名女生,现从中选3人参加某项测试赛的翻译工作,若要求这3人中既有男生,又有女生,则不同的选法共有(
)
A.120种
B.90种
C.56种
D.45种
5.已知随机变量,若,则,分别是(
)
A.6和2.4
B.2和2.4
C.4和2.4
D.4和5.6
6.已知三角形的三边长分别为,,,内切圆的半径为;则三角形的面积为;四面体的四个面的面积分别为,内切球的半径为.类比三角形的面积可得四面体的体积为
(
)
A.
B.
C.
D.
7.一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X是一个随机变量,其分布列为P(X
),则P(X=4)的值为(
)
A.
B.
C.
D.
8.已知向量.若,则x的值为(
)
A.
B.2
C.3
D.
9.100件产品中有6件次品,现从中不放回的任取3件产品,在前两次抽到正品的条件下第三次抽到次品的概率为(
)
A.
B.
C.
D.
10.一个向量在基底下的坐标为,则在基底下的坐标为(
)
A.
B.
C.
D.
11.设,那么等于(
)
A.
B.
C.
D.
12.中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“数”必须排在前三节,且“射”和“御”两门课程相邻排课,则“六艺”课程讲座不同排课顺序共有(
)
A.种
B.种
C.种
D.种
第II卷(非选择题共90分)
二、填空题(本题共20分,每题5分)
13.已知复数,则___________;
14.二项式(1﹣2x)10展开式中,第5项的二项式系数为
.
15.某一智力游戏玩一次所得的积分是一个随机变量,其概率分布如表,数学期望.则
__________.
0
3
6
16.如图,一个地区分为5个行政区域,现给该地区的地图涂色,要求相邻区域不得使用同一种颜色,现有4种颜色可供选择,则涂色方法共有
种.
三、解答题(本题共70分,17题10分,18-22每小题12分)
17.如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
18.有11个划船运动员,其中右舷手4人,左舷手5人,还有甲、乙二人左、右都能划,现要选8人组成一个划船队参加竞赛(左、右各4人),有多少种安排方法?
19.在直角坐标系中,直线,圆,以坐标原点为极点,轴正半轴为极轴建立极坐标系.
(1)求,的极坐标方程;
(2)若直线的极坐标方程为,设的交点为,求的面积.
20.有6本不同的书,在下列不同的条件下,各有多少种不同的分法?
(1)分给甲、乙、丙三人,其中一个人1本,一个人2本,一个人3本;
(2)分成三组,一组4本,另外两组各1本;
(3)甲得1本,乙得1本,丙得4本.
21.在直角坐标系中,曲线过点,其参数方程为(为参数,),以为极点,轴非负半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)求曲线的普通方程和曲线的直角坐标方程;
(2)求已知曲线和曲线交于两点,且,求实数的值.
22.随着“中华好诗词”节目的播出,掀起了全民诵读传统诗词经典的热潮.某社团为调查大学生对于“中华诗词”的喜好,从甲、乙两所大学各随机抽取了40名学生,记录他们每天学习“中华诗词”的时间,并整理得到如下频率分布直方图:
根据学生每天学习“中华诗词”的时间,可以将学生对于“中华诗词”的喜好程度分为三个等级
:
(Ⅰ)从甲大学中随机选出一名学生,试估计其“爱好”中华诗词的概率;
(Ⅱ)从两组“痴迷”的同学中随机选出2人,记为选出的两人中甲大学的人数,求的分布列和数学期望;
(Ⅲ)试判断选出的这两组学生每天学习“中华诗词”时间的平均值与的大小,及方差与的大小.(只需写出结论)
吴起高中2019-2020学年第二学期高二第三次月考
理科数学(卷)参考答案
一、单选题(本题共60分,每小题5分,每个小题只有一个正确选项)
1-6
BABDCC
7-12DADBCA
二、填空题(本题共20分,每题5分)
13、
14、210
15、
16、72
三、解答题(本题共70分,17题10分,18-22每小题12分)
17证明(1)因为是长方体,所以侧面,而平面,所以
又,,平面,因此平面;
(2)以点坐标原点,以分别为轴,建立如下图所示的空间直角坐标系,
,
因为,所以,
所以,,
设是平面的法向量,
所以,
设是平面的法向量,
所以,
二面角的余弦值的绝对值为,
所以二面角的正弦值为.
18、解:按照右舷手为标准进行分类,分三类:
第一类:右舷手4人都入选有
第二类:右舷手3人入选;则从甲乙中选一人作右舷手有
第三类:右舷手2人入选,有
所以共有
19、(1)因为,所以的极坐标方程为,
的极坐标方程为
(2)将代入
得得,
所以
因为的半径为1,则的面积为
20、解:
21、
解:(1)的参数方程,消参得普通方程为,
的极坐标方程化为即;
(2)将曲线的参数方程标准化为(为参数,)
代入曲线得,由,
得
设,对应的参数为,,由题意得即或,
当时,,解得
,
当时,解得,
综上:或.
22、(Ⅰ)
由图知,甲大学随机选取的40名学生中,“爱好”中华诗词的频率为,
所以从甲大学中随机选出一名学生,“爱好”中华诗词的概率为.
(Ⅱ)
甲大学随机选取的40名学生中“痴迷”的学生有人,
乙大学随机选取的40名学生中“痴迷”的学生有人,
所以,随机变量的取值为.
所以,
,
,
.
所以的分布列为
0
1
2
P
的数学期望为
.
(Ⅲ)
;
同课章节目录
