北师大版七年级下册数学 2.1 两条直线的位置关系课件 (第1课时 共19张PPT)
文档属性
| 名称 | 北师大版七年级下册数学 2.1 两条直线的位置关系课件 (第1课时 共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 619.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 09:25:57 | ||
图片预览




文档简介
(共19张PPT)
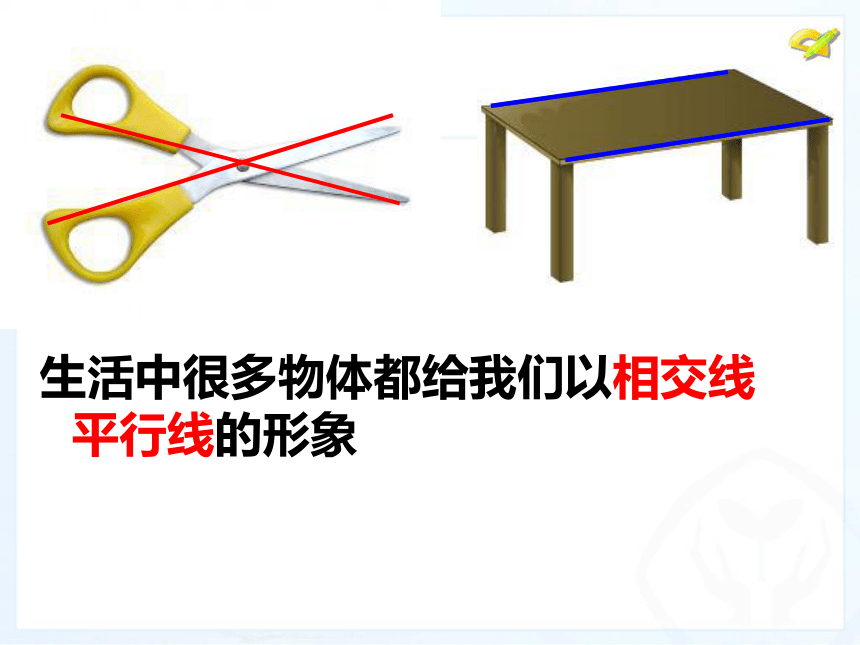
大桥上的钢梁和钢索
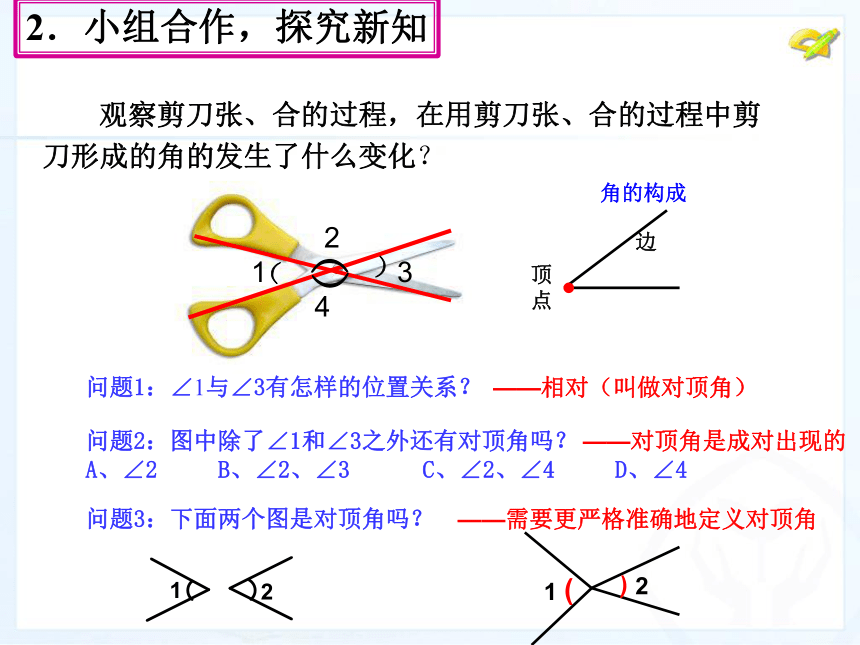
生活中很多物体都给我们以相交线平行线的形象
2.1.1两条直线的位置关第一课时
2.小组合作,探究新知
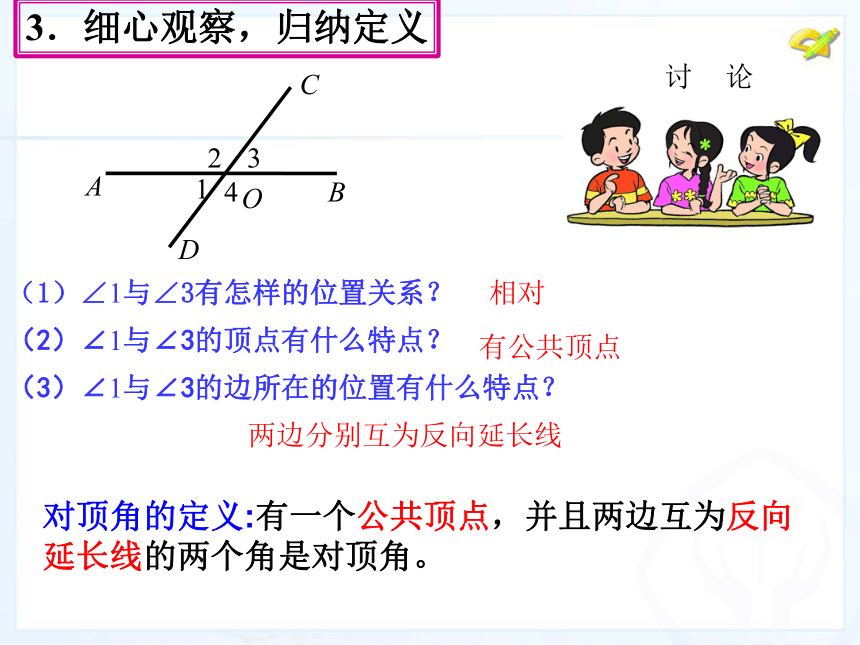
观察剪刀张、合的过程,在用剪刀张、合的过程中剪刀形成的角的发生了什么变化?
问题1:∠1与∠3有怎样的位置关系?
问题2:图中除了∠1和∠3之外还有对顶角吗?
A、∠2
B、∠2、∠3
C、∠2、∠4
D、∠4
问题3:下面两个图是对顶角吗?
——相对(叫做对顶角)
——对顶角是成对出现的
——需要更严格准确地定义对顶角
顶点
边
(1)∠1与∠3有怎样的位置关系?
(2)∠1与∠3的顶点有什么特点?
(3)∠1与∠3的边所在的位置有什么特点?
讨
论
相对
有公共顶点
两边分别互为反向延长线
3.细心观察,归纳定义
对顶角的定义:有一个公共顶点,并且两边互为反向延长线的两个角是对顶角。
(1)∠1与∠2有怎样的位置关系?
(2)∠1与∠2的顶点有什么特点?
(3)∠1与∠2的边所在的位置有什么特点?
讨
论
邻补角定义:有一条公共边,另一边互为反向延长线的两个角是邻补角。
相邻
有公共顶点
有一条公共边,另一边互为反向延长线
3.细心观察,归纳定义
1、两条相交直线形成几对邻补角?
2、∠1与∠2有怎样的数量关系?
4.动手操作,推出性质
互
补
4对
联系:补角和邻补角都是互补,邻补角是有特殊位置的两个互补的角。
区别:如果两个角是邻补角,则这两个角一定互补;反之,
如果两个角互补,则这两个角不一定是邻补角。
思考:补角与邻补角有何区别和联系呢?
1、两条相交直线形成几对对顶角?
2、∠1与∠3有怎样的数量关系?量一量。
4.动手操作,推出性质
4对
相
等
(邻补角定义)
解:
∵∠1+∠2=180°、
∠2+∠3=180°
∴∠1=∠3
同理可得:∠2=∠4
(同角的补角相等)
对顶角的性质:对顶角相等
你能用几何语言证明吗?
例1、下列各图中∠1、∠2是邻补角吗?
1、有公共顶点
2、有一条公共边
3、另一边互为反向延长线
邻补角特点:
5.例题讲解,巩固新知
例2、下列各图中∠1、∠2是对顶角吗?
1、有公共顶点
2、两边互为反向延长线
对顶角特点:
5.例题讲解,巩固新知
请在图中画出∠1的对顶角和∠2的邻补角
归纳总结
3
4
5
【小结】:一个角对顶角只有____个,
一个角的邻补角可能有____个(易漏)
一个角的补角可以有_______个
【方法】:找邻补角、对顶角关键是,找到角是由那两条直线相交形成的
知识铺垫
1
2
很多个
例3、
如图:直线AB、CD、EF相交于O
(1)∠EOA的对顶角是(
)
∠EOC的对顶角是(
)
(2)∠AOC的邻补角有(
)
∠BOE的邻补角有
(
)
(3)如果∠AOC=50
°
∠BOD
=
(
)
∠COB
=
(
)°
∠BOF
∠DOF
∠BOC、
∠AOD
∠AOE、
∠BOF
50
130
5.例题讲解,巩固新知
例4、如图,直线a、b相交,∠1=40°,求
∠2、
∠3、∠
4的度数。
解:∵
∠3=∠1(对顶角相等)
又∵∠1=40°(已知)
∴∠3=40°(等量代换)
又∵∠4+∠1=180°(邻补角的定义)
∴∠4=180°-∠1=180°-40°=140°
∴∠2=∠4=140°(对顶角的性质)
变式:若∠2是∠1的3倍,求∠3的度数?
5.例题讲解,巩固新知
当题中任何一个角都不知道度数时(标志),
常用方程思想——初中阶段常用的思想
6、当堂检测、能力提升
1、如图,直线AB、CD相交于点O,若∠AOD-∠AOC=40°,
那么∠BOD=____
2、如图,直线AB,CD,EF相交于点O,则∠1+∠2+∠3的度数为(
)
A、120°
B、90°
C、180°
D、无法计算
3、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=700,求∠BOD,∠BOC的度数。
当题中任何一个角都不知道度数时(标志),
常用方程思想——初中阶段常用的思想
4、图中是对顶角量角器,你能说出它测量角的原理吗?
对顶角相等
?5、如图1,三条直线AB、CD、
EF两两相交,在这个图形中,有
对顶角_____对,邻补角____
对.
6
12
6、如图,三条直线a、b、c两两相交,在这个图形中,有对顶角_____对,邻补角____
对.
a
b
c
6
12
6、当堂检测、能力提升
你能从中总结出数对顶角和数邻补角的方法吗?
相交线
形成
邻补角
对顶角
概念
两个角
互为
邻补角
有一条公共边
另一边互为反向延长线
概念
性质
两个角
对顶角相等
互为
对顶角
有一个公共顶点
且一个角两边分别是
另一个角两边的反向
延长线
7、课堂小结,布置作业
用知识框架的形式,谈谈你这节课收获?
1、两条直线相交于一点有___组对顶角,____邻补角;
2、三条直线相交于一点有___组对顶角,____邻补角;
3、四条直线相交于一点有___组对顶角,____邻补角;
……
4、n条直线相交于同一点有___组对顶角,____邻补角;
大桥上的钢梁和钢索
生活中很多物体都给我们以相交线平行线的形象
2.1.1两条直线的位置关第一课时
2.小组合作,探究新知
观察剪刀张、合的过程,在用剪刀张、合的过程中剪刀形成的角的发生了什么变化?
问题1:∠1与∠3有怎样的位置关系?
问题2:图中除了∠1和∠3之外还有对顶角吗?
A、∠2
B、∠2、∠3
C、∠2、∠4
D、∠4
问题3:下面两个图是对顶角吗?
——相对(叫做对顶角)
——对顶角是成对出现的
——需要更严格准确地定义对顶角
顶点
边
(1)∠1与∠3有怎样的位置关系?
(2)∠1与∠3的顶点有什么特点?
(3)∠1与∠3的边所在的位置有什么特点?
讨
论
相对
有公共顶点
两边分别互为反向延长线
3.细心观察,归纳定义
对顶角的定义:有一个公共顶点,并且两边互为反向延长线的两个角是对顶角。
(1)∠1与∠2有怎样的位置关系?
(2)∠1与∠2的顶点有什么特点?
(3)∠1与∠2的边所在的位置有什么特点?
讨
论
邻补角定义:有一条公共边,另一边互为反向延长线的两个角是邻补角。
相邻
有公共顶点
有一条公共边,另一边互为反向延长线
3.细心观察,归纳定义
1、两条相交直线形成几对邻补角?
2、∠1与∠2有怎样的数量关系?
4.动手操作,推出性质
互
补
4对
联系:补角和邻补角都是互补,邻补角是有特殊位置的两个互补的角。
区别:如果两个角是邻补角,则这两个角一定互补;反之,
如果两个角互补,则这两个角不一定是邻补角。
思考:补角与邻补角有何区别和联系呢?
1、两条相交直线形成几对对顶角?
2、∠1与∠3有怎样的数量关系?量一量。
4.动手操作,推出性质
4对
相
等
(邻补角定义)
解:
∵∠1+∠2=180°、
∠2+∠3=180°
∴∠1=∠3
同理可得:∠2=∠4
(同角的补角相等)
对顶角的性质:对顶角相等
你能用几何语言证明吗?
例1、下列各图中∠1、∠2是邻补角吗?
1、有公共顶点
2、有一条公共边
3、另一边互为反向延长线
邻补角特点:
5.例题讲解,巩固新知
例2、下列各图中∠1、∠2是对顶角吗?
1、有公共顶点
2、两边互为反向延长线
对顶角特点:
5.例题讲解,巩固新知
请在图中画出∠1的对顶角和∠2的邻补角
归纳总结
3
4
5
【小结】:一个角对顶角只有____个,
一个角的邻补角可能有____个(易漏)
一个角的补角可以有_______个
【方法】:找邻补角、对顶角关键是,找到角是由那两条直线相交形成的
知识铺垫
1
2
很多个
例3、
如图:直线AB、CD、EF相交于O
(1)∠EOA的对顶角是(
)
∠EOC的对顶角是(
)
(2)∠AOC的邻补角有(
)
∠BOE的邻补角有
(
)
(3)如果∠AOC=50
°
∠BOD
=
(
)
∠COB
=
(
)°
∠BOF
∠DOF
∠BOC、
∠AOD
∠AOE、
∠BOF
50
130
5.例题讲解,巩固新知
例4、如图,直线a、b相交,∠1=40°,求
∠2、
∠3、∠
4的度数。
解:∵
∠3=∠1(对顶角相等)
又∵∠1=40°(已知)
∴∠3=40°(等量代换)
又∵∠4+∠1=180°(邻补角的定义)
∴∠4=180°-∠1=180°-40°=140°
∴∠2=∠4=140°(对顶角的性质)
变式:若∠2是∠1的3倍,求∠3的度数?
5.例题讲解,巩固新知
当题中任何一个角都不知道度数时(标志),
常用方程思想——初中阶段常用的思想
6、当堂检测、能力提升
1、如图,直线AB、CD相交于点O,若∠AOD-∠AOC=40°,
那么∠BOD=____
2、如图,直线AB,CD,EF相交于点O,则∠1+∠2+∠3的度数为(
)
A、120°
B、90°
C、180°
D、无法计算
3、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=700,求∠BOD,∠BOC的度数。
当题中任何一个角都不知道度数时(标志),
常用方程思想——初中阶段常用的思想
4、图中是对顶角量角器,你能说出它测量角的原理吗?
对顶角相等
?5、如图1,三条直线AB、CD、
EF两两相交,在这个图形中,有
对顶角_____对,邻补角____
对.
6
12
6、如图,三条直线a、b、c两两相交,在这个图形中,有对顶角_____对,邻补角____
对.
a
b
c
6
12
6、当堂检测、能力提升
你能从中总结出数对顶角和数邻补角的方法吗?
相交线
形成
邻补角
对顶角
概念
两个角
互为
邻补角
有一条公共边
另一边互为反向延长线
概念
性质
两个角
对顶角相等
互为
对顶角
有一个公共顶点
且一个角两边分别是
另一个角两边的反向
延长线
7、课堂小结,布置作业
用知识框架的形式,谈谈你这节课收获?
1、两条直线相交于一点有___组对顶角,____邻补角;
2、三条直线相交于一点有___组对顶角,____邻补角;
3、四条直线相交于一点有___组对顶角,____邻补角;
……
4、n条直线相交于同一点有___组对顶角,____邻补角;
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
