相似判定一

(共33张PPT)
学习目标：
1、了解相似多边形的概念；认识相似多边形；
2、会识别两个相似多边形的对应角及对应边；
3、了解相似多边形的性质及应用其解决一些简单问题；
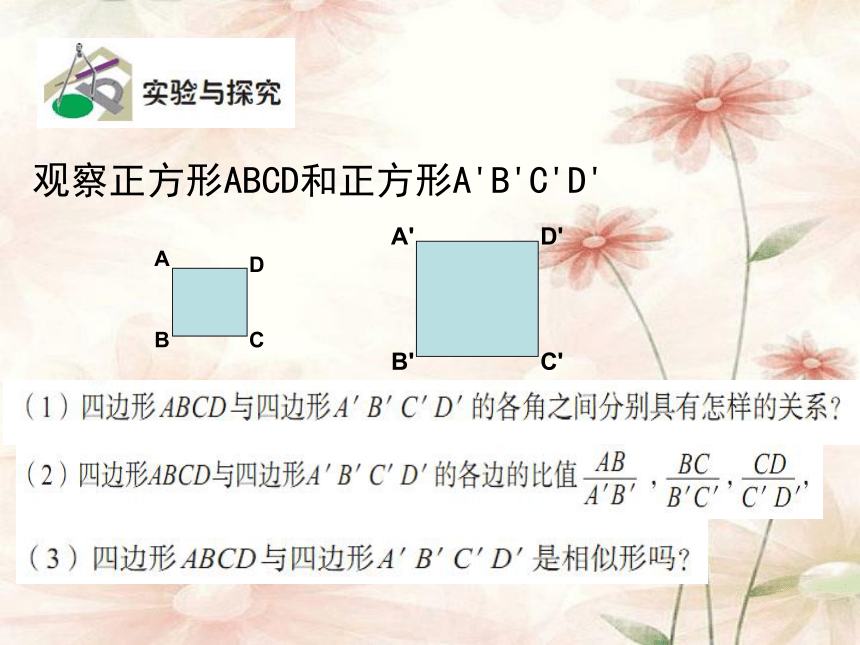
观察正方形ABCD和正方形A'B'C'D'
A
B
C
D
A'
B'
C'
D'
相似多边形的条件：
1、边数相同；
2、各个角对应相等；
3、各边对应成比例；
相似多边形的性质：
交流与发现
猜猜看，与同学交流.
合作探究
合作探究
一般地，从两个相似多边形一对对应顶点各自
引出的对角线，把两个多边形分成个数相同的三角
形，相应的三角形分别相似，并且它们的对应边的
比不变。由于相似三角形面积的比等于相似三角形
对应边的比的平方，利用比例的性质可以得到:
相似多边形面积的比等于它们对应边的比的平方.
知识梳理
相似多边形周长的比等于它们对应边的比.
实验与探究
(1)四边形ABCD与四边形A′B'C′D′的各角之间分别具有怎样的关系?
2)四边形ABCD与四边形A′B'C′D′的各边的比值
AB
BC
CD
ABB′C′C′D
(3)四边形ABCD与四边形A′B′C′D是相似形吗?
如果两个多边形的边数相同,并且一个多边形的各个角分别与另一个多边形
的各个角对应相等,各边对应成比例,那么这两个多边形叫做相似多边形(
similar
polygons
四边形ABCD与四边形AB'CD相似,记作四边形ABCD∽四边形AB'CD
例1如图8-36,已知四边形ABCD∽四边形AB'CD′,AD=18,CD
21,A′D=24,∠A=65°,∠B=85°,∠C=60°求
C
B
图8-36
(1)∠A,∠B,∠C及∠D'的度数;
(2)C′D′的长
例1如图8-36,已知四边形ABCD∽四边形AB'CD′,AD=18,CD
21,A'D′=24,∠A=65°,∠B=85°,∠C=60°求
(1)∠A,∠B,∠C及∠D’的度数
(2)C′D′的长
B
图8-36
∠D′=(4-2)·180°-∠A′-∠B′-∠C′=360°-65°-85°-60°
(2)因为四边形ABCD∽四边形A'B′C′D′,由于相似多边形的对应边成比
AD
CD
21
例,所以
于是
,求得C′D′=28
AD′C′D
24
C
D
解(1)因为四边形ABCD∽四边形ABC'D,由于相似多边形的对
如图8-37,五边形
ABCDE∽五边形AB'C'DE′,如果对应边的比为k,那