人教版数学八年级下册:19.2.1 正比例函数及其图像 课件(共40张PPT)
文档属性
| 名称 | 人教版数学八年级下册:19.2.1 正比例函数及其图像 课件(共40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 767.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-24 08:06:16 | ||
图片预览





文档简介
(共40张PPT)
常量和变量
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
知识回顾:
一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
知识回顾:
函数
前提条件是:
1、两个变量之间的对应关系是“x的每一个确定的值,y都有唯一确定的值与其对应”.
2、一个变化过程中只有两个变量.
3、“x的每一个确定的值”中的“确定”是指x的取值要符合变化过程的实际意义.
练习:
选B.
将第一象限或第三象限的曲线去掉等,只要满足“对于x的每一个确定的值,y都有唯一确定的值与其对应”,都能使y是x的函数.
下列曲线中,表示y不是x的函数是(
),怎样改动这条曲线,才能使y是x的函数?
A
x
y
O
B
x
y
O
C
x
y
O
D
x
y
O
练习:
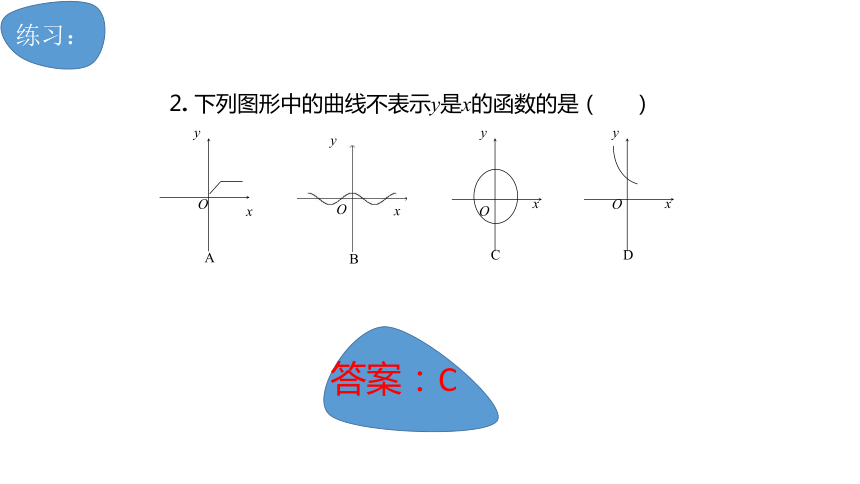
2.
下列图形中的曲线不表示y是x的函数的是(
)
y
x
O
D
y
x
O
A
y
x
O
C
y
O
B
x
答案:C
知识回顾:
函数图像的画法(描点法)
1、列表
2、描点(5到7个为宜)
3、连线(平滑曲线链接)
表达式
列表
x
y
(横坐标,纵坐标)
(x,y)
例如:
点(3,
5)在函数
y=2x+b
上,求
b
的值.
x
y
练习:
点
(x,y)
知识回顾:
函数的表示方法
1、解析式法
2、列表法
3、图像法
知识回顾:
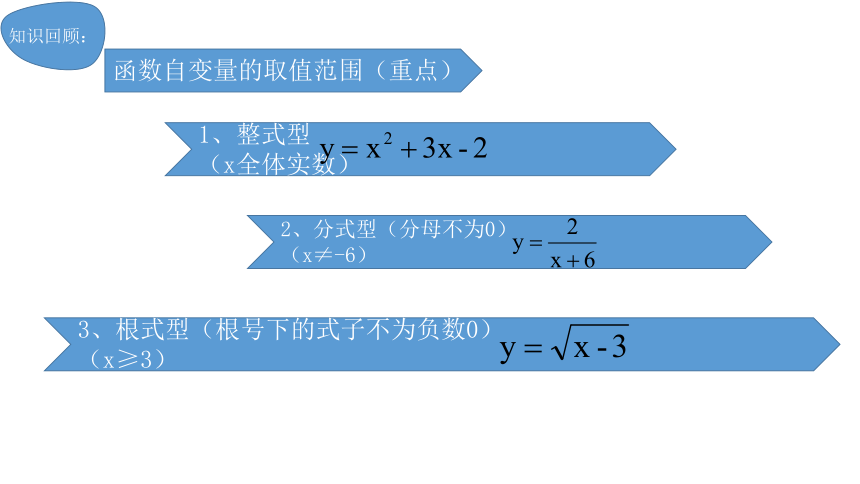
函数自变量的取值范围(重点)
1、整式型
(x全体实数)
2、分式型(分母不为0)
(x≠-6)
3、根式型(根号下的式子不为负数0)
(x≥3)
求下列函数中自变量x的取值范围:
练习:
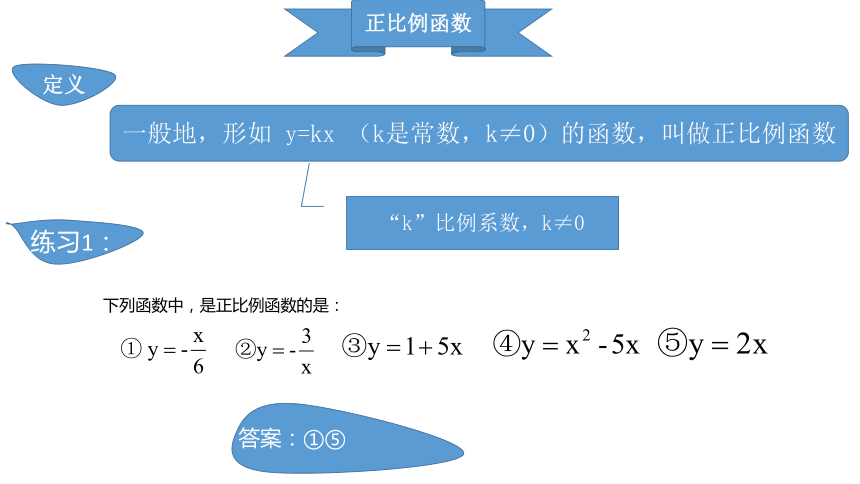
正比例函数
定义
一般地,形如
y=kx
(k是常数,k≠0)的函数,叫做正比例函数
“k”比例系数,k≠0
下列函数中,是正比例函数的是:
答案:①⑤
练习1:
下列式子,哪些表示y是x的正比例函数?如果是,请你指出正比例系数k的值.
(1)y=-0.1x
(2)
(3)y=2x2
(4)y2=4x
(5)y=-4x+3
(6)y=2(x-x2
)+2x2
是正比例函数,
正比例系数为-0.1
是正比例函数,
正比例系数为0.5
不是正比例函数
不是正比例函数
不是正比例函数
是正比例函数,正比例系数为2
判定一个函数是否是正比例函数,要从化简后来判断!
练习2:
列式表示下列问题中y与x的函数关系,并指出哪些是正比例函数.
(1)正方形的边长为xcm,周长为ycm.
y=4x
是正比例函数
(2)某人一年内的月平均收入为x元,他这年(12个月)的总收入为y元.
y=12x
是正比例函数
(3)一个长方体的长为2cm,宽为1.5cm,高为xcm
,体积为ycm3.
y=3x
是正比例函数
练习3:
下列说法正确的打“√”,错误的打“×”
(1)若y=kx,则y是x的正比例函数(
)
(2)若y=2x2,则y是x的正比例函数(
)
(3)若y=2(x-1)+2,则y是x的正比例函数(
)
(4)若y=2(x-1)
,则y是x-1的正比例函数(
)
×
×
√
在特定条件下自变量可能不单独就是x了,要注意自变量的变化
√
练习4:
练习5:
已知
是正比例函数,求a的值.
解:∵
是正比例函数,
∴a=-1
(1)如果y=(k-1)x,是y关于x的正比例函数,则k满足________________.
(2)如果y=kxk-1,是y关于x的正比例函数,则k=__________.
(3)如果y=3x+k-4,是y关于x的正比例函数,则k=_________.
k≠1
2
4
练习6:
练习7:运用概念
(1)已知正比例函数y=kx,当x=3时,y=-15,求k的值.
(2)若y关于x成正比例函数,当x=4时,y=-2.
①求出y与x的关系式;
②当x=6时,求出对应的函数值y.
k=-5
y=
-0.5x
y=
-3
你如何理解正比例函数的意义?能从哪几个方面去认识正比例函数?
1.从语言描述看:
函数关系式是常量与自变量的乘积.
2.从外形特征看:
(1)一般情况下y=kx(常数k≠0);
(2)在特定条件下自变量可能不单独是x了,要注意问题中自变量的变化.
3.从结果形式看:
函数表达式要化简后才能确认为正比例函数
正比例函数
y=kx
(k是常数,k≠0)的深刻理解:
(1)如果y=(k-1)x,是y关于x的正比例函数,则k满足___________.
(2)如果y=kxk-1,是y关于x的正比例函数,则k=__________.
(3)如果y=3x+k-4,是y关于x的正比例函数,则k=_________.
(4)已知正比例函数y=kx,当x=3时,y=-15,求k的值.
(5)若y关于x成正比例函数,当x=4时,y=-2.
①求出y与x的关系式;
②当x=6时,求出对应的函数值y.
练习6:
k≠1
2
4
k=-5
y=
-0.5x
y=
-3
(6)关于y
=
说法正确的是(
)
A.是y关于x的正比例函数,正比例系数为-2
B.是y关于x的正比例函数,正比例系数为
C.是y关于x+3的正比例函数,正比例系数为-2
D.是y关于x+3的正比例函数,正比例系数为
(7)若y=kx+2k-3是y关于x的正比例函数,则k=______________.
(8)若y=(k-2)x是y关于x的正比例函数,则k满足的条件是______________.
(9)已知y关于x成正比例函数,当x=3时,y=-9,则y与x的关系式为_______.
练习6:
(10)若y=(k+3)x|k|-2是y关于x的正比例函数,试求k的值,并指出正比例系数.
(11)若y关于x-2成正比例函数,当x=3时,y=-4.试求出y与x的函数关系式.
练习6:
正比例函数
y=kx
(k≠0)的图像
活动一:创设情境
1.在下列函数中,哪些是正比例函数?并指出正比例系数分别是多少.
①y=x,
②y=3x2,
③
y=2x
,
④y=2x-4,
⑤
,
⑥y=-x
,
⑦y=-2x.
y=x,正比例系数为1
y=-x,正比例系数为-1
y=-2x,正比例系数为-2
y=2x,正比例系数为2
活动一:创设情境
2.画函数图象需要经历哪些步骤?
3.你能依据这些步骤画出以上正比例函数的图象吗?
列表、描点、连线
活动二:画函数图象
x
…
-3
-2
-1
0
1
2
3
…
y
…
…
1.正比例函数y=x的自变量取值范围是什么?你能取完自变量x的所有值吗?
2.如果不能,你认为在列出的表格中自变量x取哪些值合适?
2.描点;
4.观察这些点的摆放有何规律?
5.你能保证以上两点之间一定靠直线连接的吗?以点(0,0)与(1,1)之间为例,为什么是靠直线连接的呢?
1.列表;
3.连线.
-3
-2
-1
0
1
2
3
活动二:画函数图象
在(0,0)与(1,1)之间描出十等分点,画出y=x的图象的一段.
x
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
y
0
1
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
O
活动二:画函数图象
活动二:画函数图象
在(0,0)与(1,1)之间描出二十等分点,画出y=x的图象的一段;(表格在前面的基础上加下列)
x
0
0.05
0.15
0.25
0.35
0.45
0.55
0.65
0.75
0.85
0.95
y
0.05
0.15
0.25
0.35
0.45
0.55
0.65
0.75
0.85
0.95
0
O
活动二:画函数图象
6.如果我们不断找下去,找一百等分点呢?一千等分点呢?可以发现(0,0)与(1,1)之间是靠什么线连接的,那么其他两个整数点之间靠什么线连接的呢?表格中省略号是什么意思?
7.你发现正比例函数y=x的图象是什么?
直线
活动二:画函数图象
y
-4
-2
-3
-1
3
2
1
-1
O
-2
-3
1
2
3
4
5
x
-4
-2
0
2
4
y=2x
x
…
-2
-1
0
1
2
…
y
画正比例函数
y
=2x
的图象.
解:
1.
列表
2.
描点
3.
连线
…
…
y=x
活动二:画函数图象
y
-4
-2
-3
-1
3
2
1
-1
O
-2
-3
1
2
3
4
5
x
4
2
0
-2
-4
y=-2x
x
…
-2
-1
0
1
2
…
y=-x
y=-2x
画正比例函数y=-x和y=-2x的图象.
解:
1.
列表
2.
描点
3.
连线
…
…
y=-x
2
1
0
-1
2
活动二:画函数图象
活动三:
总结性质
1.正比例函数的图象都是经过_______的直线,那么你画正比例函数有什么简便方法?为什么?你一般选取哪些点画它的图象呢?
2.在画函数图象时,使函数图象位置发生变化的量是x、y、k中的哪个量?
3.这个量是如何影响正比例函数函数值的变化?又是如何影响正比例函数图象的呢?请你分情况具体说一说.
原点
选两点坐标就可以,一般选(0,0)和(1,k)
k
(1)当k>0时,y随x的增大而增大,直线经过一、三象限,
从左到右是上升的;
(2)当k<0时,y随x的增大而减小,直线经过二、四象限,
从左到右是下降的.
活动三:
总结性质
4.为什么k>0时,图象会经过一、三象限?而k<0时,图象却经过二、四象限?
5.当正比例函数图象经过一、三象限时,你能获得哪些信息?经过二、四象限呢?
(1)当k>0时,x为正数,y也是正数,故在第一象限;x=0,
y=0,故经过原点;x为负数,y也是负数,故在第三象限;所
以,k>0时,图象经过一、三象限.(2)反之,k<0时,图象经过二、四象限.
(1)当图象经过一、三象限时,k>0,y随x的增大而增大,图象从左到右是上升的.
(2)当图象经过二、四象限时,k<0,y随x的增大而减小,图象从左到右是下降的.
活动三:
总结性质
6.你还发现哪些性质?
(1)当图象经过一、三象限时,直线与x轴正方向的夹角越大,k值就越大;
(2)当图象经过二、四象限时,直线与x轴负方向的夹角越大,k值就越小;
O
活动四:初步练习
用你认为最简单的方法画出下列函数的图象:
(1)
y=-3x;(2)
x
0
1
y=-3x
0
-3
0
y=-3x
活动五:巩固练习
1.若正比例函数y=(k-3)x满足下列条件,求出k的范围.
(1)y
随x的增大而增大;
(2)图象经过一、三象限;
(3)图象如图所示.
k>3
k>3
k<3
O
x
y
活动五:巩固练习
2.下列图象中是y=-1.2x函数图象的是(
)
D
y
y
y
y
x
x
x
x
C
B
A
O
O
O
D
O
活动六:
课堂小结与作业布置
1.从数看:若正比例函数y=kx(k≠0),k对函数值得变化又有何影响呢?对函数图象有何影响呢?
2.从形看:若正比例函数y=kx(k≠0)的图象经过一、三象限,那么你可以得出什么信息?反之,若经过二、四象限呢?
(1)当k>0时,y随x的增大而增大,直线经过一、三象限,从左到
右是上升的;
(2)当k<0时,y随x的增大而减小,直线经过二、四象限,从左到右是下降的.
(1)当图象经过一、三象限时,k>0,y随x的增大而增大,图象从左到右是上升的.
(2)当图象经过二、四象限时,k<0,y随x的增大而减小,图象从左到右是下降的.
作业
1.
教材习题19.2第1、2题
.
补充:1.已知
y关于x的正比例函数
y=(2-k)x的图象经过一、三象限,则
对y关于x的
函数y=(k-3)x的说法不正确的是(
)
A.图象是经过原点的直线
B.
y随x的增大而减小
C.图象经过二、四象限
D.图象从左到右呈上升趋势
2.已知
y关于x的正比例函数
y=(k+3)x|k|-4,且
y随x的增大而减小,那么k=________.
3.若
y=k1x,y=k2x,y=k3x,y=k4x的图象如图所示,
则下列不等关系正确的是(
)
A.k1B.k2C.k4D.k4O
x
y
常量和变量
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
知识回顾:
一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
知识回顾:
函数
前提条件是:
1、两个变量之间的对应关系是“x的每一个确定的值,y都有唯一确定的值与其对应”.
2、一个变化过程中只有两个变量.
3、“x的每一个确定的值”中的“确定”是指x的取值要符合变化过程的实际意义.
练习:
选B.
将第一象限或第三象限的曲线去掉等,只要满足“对于x的每一个确定的值,y都有唯一确定的值与其对应”,都能使y是x的函数.
下列曲线中,表示y不是x的函数是(
),怎样改动这条曲线,才能使y是x的函数?
A
x
y
O
B
x
y
O
C
x
y
O
D
x
y
O
练习:
2.
下列图形中的曲线不表示y是x的函数的是(
)
y
x
O
D
y
x
O
A
y
x
O
C
y
O
B
x
答案:C
知识回顾:
函数图像的画法(描点法)
1、列表
2、描点(5到7个为宜)
3、连线(平滑曲线链接)
表达式
列表
x
y
(横坐标,纵坐标)
(x,y)
例如:
点(3,
5)在函数
y=2x+b
上,求
b
的值.
x
y
练习:
点
(x,y)
知识回顾:
函数的表示方法
1、解析式法
2、列表法
3、图像法
知识回顾:
函数自变量的取值范围(重点)
1、整式型
(x全体实数)
2、分式型(分母不为0)
(x≠-6)
3、根式型(根号下的式子不为负数0)
(x≥3)
求下列函数中自变量x的取值范围:
练习:
正比例函数
定义
一般地,形如
y=kx
(k是常数,k≠0)的函数,叫做正比例函数
“k”比例系数,k≠0
下列函数中,是正比例函数的是:
答案:①⑤
练习1:
下列式子,哪些表示y是x的正比例函数?如果是,请你指出正比例系数k的值.
(1)y=-0.1x
(2)
(3)y=2x2
(4)y2=4x
(5)y=-4x+3
(6)y=2(x-x2
)+2x2
是正比例函数,
正比例系数为-0.1
是正比例函数,
正比例系数为0.5
不是正比例函数
不是正比例函数
不是正比例函数
是正比例函数,正比例系数为2
判定一个函数是否是正比例函数,要从化简后来判断!
练习2:
列式表示下列问题中y与x的函数关系,并指出哪些是正比例函数.
(1)正方形的边长为xcm,周长为ycm.
y=4x
是正比例函数
(2)某人一年内的月平均收入为x元,他这年(12个月)的总收入为y元.
y=12x
是正比例函数
(3)一个长方体的长为2cm,宽为1.5cm,高为xcm
,体积为ycm3.
y=3x
是正比例函数
练习3:
下列说法正确的打“√”,错误的打“×”
(1)若y=kx,则y是x的正比例函数(
)
(2)若y=2x2,则y是x的正比例函数(
)
(3)若y=2(x-1)+2,则y是x的正比例函数(
)
(4)若y=2(x-1)
,则y是x-1的正比例函数(
)
×
×
√
在特定条件下自变量可能不单独就是x了,要注意自变量的变化
√
练习4:
练习5:
已知
是正比例函数,求a的值.
解:∵
是正比例函数,
∴a=-1
(1)如果y=(k-1)x,是y关于x的正比例函数,则k满足________________.
(2)如果y=kxk-1,是y关于x的正比例函数,则k=__________.
(3)如果y=3x+k-4,是y关于x的正比例函数,则k=_________.
k≠1
2
4
练习6:
练习7:运用概念
(1)已知正比例函数y=kx,当x=3时,y=-15,求k的值.
(2)若y关于x成正比例函数,当x=4时,y=-2.
①求出y与x的关系式;
②当x=6时,求出对应的函数值y.
k=-5
y=
-0.5x
y=
-3
你如何理解正比例函数的意义?能从哪几个方面去认识正比例函数?
1.从语言描述看:
函数关系式是常量与自变量的乘积.
2.从外形特征看:
(1)一般情况下y=kx(常数k≠0);
(2)在特定条件下自变量可能不单独是x了,要注意问题中自变量的变化.
3.从结果形式看:
函数表达式要化简后才能确认为正比例函数
正比例函数
y=kx
(k是常数,k≠0)的深刻理解:
(1)如果y=(k-1)x,是y关于x的正比例函数,则k满足___________.
(2)如果y=kxk-1,是y关于x的正比例函数,则k=__________.
(3)如果y=3x+k-4,是y关于x的正比例函数,则k=_________.
(4)已知正比例函数y=kx,当x=3时,y=-15,求k的值.
(5)若y关于x成正比例函数,当x=4时,y=-2.
①求出y与x的关系式;
②当x=6时,求出对应的函数值y.
练习6:
k≠1
2
4
k=-5
y=
-0.5x
y=
-3
(6)关于y
=
说法正确的是(
)
A.是y关于x的正比例函数,正比例系数为-2
B.是y关于x的正比例函数,正比例系数为
C.是y关于x+3的正比例函数,正比例系数为-2
D.是y关于x+3的正比例函数,正比例系数为
(7)若y=kx+2k-3是y关于x的正比例函数,则k=______________.
(8)若y=(k-2)x是y关于x的正比例函数,则k满足的条件是______________.
(9)已知y关于x成正比例函数,当x=3时,y=-9,则y与x的关系式为_______.
练习6:
(10)若y=(k+3)x|k|-2是y关于x的正比例函数,试求k的值,并指出正比例系数.
(11)若y关于x-2成正比例函数,当x=3时,y=-4.试求出y与x的函数关系式.
练习6:
正比例函数
y=kx
(k≠0)的图像
活动一:创设情境
1.在下列函数中,哪些是正比例函数?并指出正比例系数分别是多少.
①y=x,
②y=3x2,
③
y=2x
,
④y=2x-4,
⑤
,
⑥y=-x
,
⑦y=-2x.
y=x,正比例系数为1
y=-x,正比例系数为-1
y=-2x,正比例系数为-2
y=2x,正比例系数为2
活动一:创设情境
2.画函数图象需要经历哪些步骤?
3.你能依据这些步骤画出以上正比例函数的图象吗?
列表、描点、连线
活动二:画函数图象
x
…
-3
-2
-1
0
1
2
3
…
y
…
…
1.正比例函数y=x的自变量取值范围是什么?你能取完自变量x的所有值吗?
2.如果不能,你认为在列出的表格中自变量x取哪些值合适?
2.描点;
4.观察这些点的摆放有何规律?
5.你能保证以上两点之间一定靠直线连接的吗?以点(0,0)与(1,1)之间为例,为什么是靠直线连接的呢?
1.列表;
3.连线.
-3
-2
-1
0
1
2
3
活动二:画函数图象
在(0,0)与(1,1)之间描出十等分点,画出y=x的图象的一段.
x
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
y
0
1
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
O
活动二:画函数图象
活动二:画函数图象
在(0,0)与(1,1)之间描出二十等分点,画出y=x的图象的一段;(表格在前面的基础上加下列)
x
0
0.05
0.15
0.25
0.35
0.45
0.55
0.65
0.75
0.85
0.95
y
0.05
0.15
0.25
0.35
0.45
0.55
0.65
0.75
0.85
0.95
0
O
活动二:画函数图象
6.如果我们不断找下去,找一百等分点呢?一千等分点呢?可以发现(0,0)与(1,1)之间是靠什么线连接的,那么其他两个整数点之间靠什么线连接的呢?表格中省略号是什么意思?
7.你发现正比例函数y=x的图象是什么?
直线
活动二:画函数图象
y
-4
-2
-3
-1
3
2
1
-1
O
-2
-3
1
2
3
4
5
x
-4
-2
0
2
4
y=2x
x
…
-2
-1
0
1
2
…
y
画正比例函数
y
=2x
的图象.
解:
1.
列表
2.
描点
3.
连线
…
…
y=x
活动二:画函数图象
y
-4
-2
-3
-1
3
2
1
-1
O
-2
-3
1
2
3
4
5
x
4
2
0
-2
-4
y=-2x
x
…
-2
-1
0
1
2
…
y=-x
y=-2x
画正比例函数y=-x和y=-2x的图象.
解:
1.
列表
2.
描点
3.
连线
…
…
y=-x
2
1
0
-1
2
活动二:画函数图象
活动三:
总结性质
1.正比例函数的图象都是经过_______的直线,那么你画正比例函数有什么简便方法?为什么?你一般选取哪些点画它的图象呢?
2.在画函数图象时,使函数图象位置发生变化的量是x、y、k中的哪个量?
3.这个量是如何影响正比例函数函数值的变化?又是如何影响正比例函数图象的呢?请你分情况具体说一说.
原点
选两点坐标就可以,一般选(0,0)和(1,k)
k
(1)当k>0时,y随x的增大而增大,直线经过一、三象限,
从左到右是上升的;
(2)当k<0时,y随x的增大而减小,直线经过二、四象限,
从左到右是下降的.
活动三:
总结性质
4.为什么k>0时,图象会经过一、三象限?而k<0时,图象却经过二、四象限?
5.当正比例函数图象经过一、三象限时,你能获得哪些信息?经过二、四象限呢?
(1)当k>0时,x为正数,y也是正数,故在第一象限;x=0,
y=0,故经过原点;x为负数,y也是负数,故在第三象限;所
以,k>0时,图象经过一、三象限.(2)反之,k<0时,图象经过二、四象限.
(1)当图象经过一、三象限时,k>0,y随x的增大而增大,图象从左到右是上升的.
(2)当图象经过二、四象限时,k<0,y随x的增大而减小,图象从左到右是下降的.
活动三:
总结性质
6.你还发现哪些性质?
(1)当图象经过一、三象限时,直线与x轴正方向的夹角越大,k值就越大;
(2)当图象经过二、四象限时,直线与x轴负方向的夹角越大,k值就越小;
O
活动四:初步练习
用你认为最简单的方法画出下列函数的图象:
(1)
y=-3x;(2)
x
0
1
y=-3x
0
-3
0
y=-3x
活动五:巩固练习
1.若正比例函数y=(k-3)x满足下列条件,求出k的范围.
(1)y
随x的增大而增大;
(2)图象经过一、三象限;
(3)图象如图所示.
k>3
k>3
k<3
O
x
y
活动五:巩固练习
2.下列图象中是y=-1.2x函数图象的是(
)
D
y
y
y
y
x
x
x
x
C
B
A
O
O
O
D
O
活动六:
课堂小结与作业布置
1.从数看:若正比例函数y=kx(k≠0),k对函数值得变化又有何影响呢?对函数图象有何影响呢?
2.从形看:若正比例函数y=kx(k≠0)的图象经过一、三象限,那么你可以得出什么信息?反之,若经过二、四象限呢?
(1)当k>0时,y随x的增大而增大,直线经过一、三象限,从左到
右是上升的;
(2)当k<0时,y随x的增大而减小,直线经过二、四象限,从左到右是下降的.
(1)当图象经过一、三象限时,k>0,y随x的增大而增大,图象从左到右是上升的.
(2)当图象经过二、四象限时,k<0,y随x的增大而减小,图象从左到右是下降的.
作业
1.
教材习题19.2第1、2题
.
补充:1.已知
y关于x的正比例函数
y=(2-k)x的图象经过一、三象限,则
对y关于x的
函数y=(k-3)x的说法不正确的是(
)
A.图象是经过原点的直线
B.
y随x的增大而减小
C.图象经过二、四象限
D.图象从左到右呈上升趋势
2.已知
y关于x的正比例函数
y=(k+3)x|k|-4,且
y随x的增大而减小,那么k=________.
3.若
y=k1x,y=k2x,y=k3x,y=k4x的图象如图所示,
则下列不等关系正确的是(
)
A.k1
x
y
