人教版九年级数学下册 28.2.1 解直角三角形课件(21张ppt)
文档属性
| 名称 | 人教版九年级数学下册 28.2.1 解直角三角形课件(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 20:07:57 | ||
图片预览








文档简介
(共21张PPT)
28
28.2.1
解直角三角形
锐角三角函数
学习目标
教学分析
1.理解直角三角形中五个元素的关系,会运用勾股定理,
直角三角形的两个锐角互余及锐角三角函数解直角三角形;
2.渗透数形结合的数学思想,培养良好的学习习惯.
导入新课
在Rt△ABC
中,共有六个元素(三条边,三个角),其中∠C
=90°,
那么其余五个元素之间有怎样的关系呢?
A
C
B
c
b
a
(1)
三边之间的关系:a
2+b
2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:
sinA=
,cosA
=
,tanA
=
.
c
2
90°
合作探究
探究点一
解直角三角形的定义
合作探究
如图,设塔顶中心点为B,
塔身中心线与垂直中心线的夹角为∠A,
过B点向垂直中心线引垂线,垂足为点C.
在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m.
根据以上条件可以求出塔身中心线
与垂直中心线的夹角.
你愿意试着计算一下吗?
合作探究
解:
利用计算器可得
.
将上述问题推广到一般情形,
就是:
已知直角三角形的斜边和一条直角边,
求它的锐角的度数.
合作探究
A
B
C
30
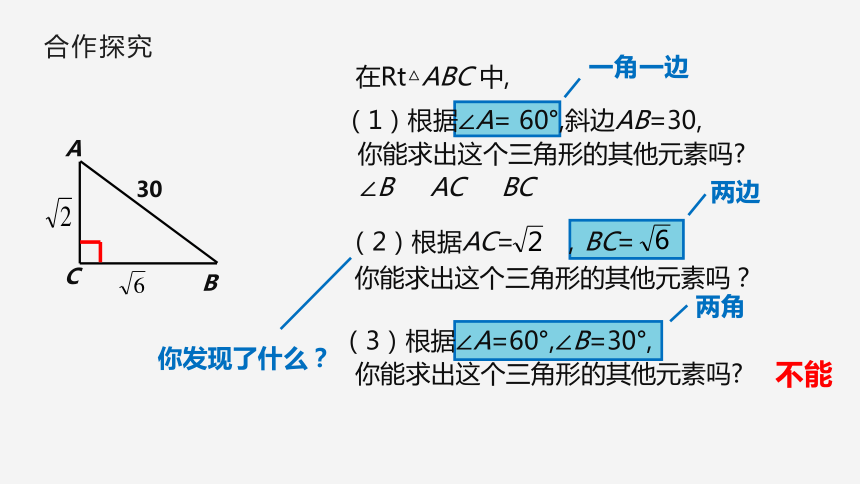
在Rt△ABC
中,
(2)根据AC=
,BC=
你能求出这个三角形的其他元素吗?
(1)根据∠A=
60°,斜边AB=30,
∠B
AC
BC
你能求出这个三角形的其他元素吗?
(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元素吗?
一角一边
两边
不能
两角
你发现了什么?
合作探究
在直角三角形的六个元素中,
除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
合作探究
定义:
在直角三角形中,由已知元素
求出其余未知元素的过程,
叫做解直角三角形.
合作探究
A
B
a
b
c
C
在解直角三角形的过程中,一般
要用到下面一些关系:
(1)三边之间的关系
a2+b2=c2
(勾股定理)
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
合作探究
A
B
a
b
c
C
合作探究
探究点二
解直角三角形
合作探究
例
1
如图,在Rt△ABC
中,∠C=90°,解这个直角三角形.
A
B
C
解:
合作探究
例
2
如图,在Rt△ABC
中,∠B=35°,b=20,
解这个直角三角形(结果保留小数点后一位).
A
B
C
a
b
=
c
20
35°
解:
你还有其他方法求出c
吗?
合作探究
针对训练
如图,从点C
测得树的顶角为33?,BC=20米,
则树高AB=________米(用计算器计算,结果精确到0.1米).
解析:
AB=BC·tanC=20×tan33°=13.0.
答案:
13.0
13.0
课堂小结
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形,
当图形中没有直角三角形时,要通过作辅助线构造直角三角形
(作某边上的高是常用的辅助线).
2.一些解直角三角形的问题往往与其他知识联系,
所以在复习时要形成知识结构,要把解直角三角形作为一种工具,
能在解决各种数学问题时合理运用.
巩固拓展
1.在下列直角三角形中不能求解的是(
)
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角
D
2.边长为6cm的等边三角形中,其一边上高的长度
为________cm.
解析:
一边上的高=6×sin60°=
(cm).
巩固拓展
3.如图,小明为了测量其所在位置,A点到河对岸B点之间的
距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,
那么AB等于(
)
A
B
C
m
A.
m·sinα米
B.m·tanα米
C.m·cosα米
D.
米
B
巩固拓展
4.已知:如图,在Rt△ABC
中,
∠C=90°,AC=
.
点D
为BC
边上一点,
且BD=2AD,∠ADC=60°,
求△ABC
的周长(结果保留根号).
巩固拓展
解析:
要求△ABC
的周长,
只要求得BC
及AB
的长度即可.
根据Rt△ADC
中∠ADC
的正弦值
和AC
的长度,可以求得AD
的长度,
也可求得CD
的长度;
再根据已知条件求得BD
的长度,
继而求得BC
的长度;
运用勾股定理可以求得AB
的长度,
最后求得△ABC
的周长.
巩固拓展
解:
28
28.2.1
解直角三角形
锐角三角函数
学习目标
教学分析
1.理解直角三角形中五个元素的关系,会运用勾股定理,
直角三角形的两个锐角互余及锐角三角函数解直角三角形;
2.渗透数形结合的数学思想,培养良好的学习习惯.
导入新课
在Rt△ABC
中,共有六个元素(三条边,三个角),其中∠C
=90°,
那么其余五个元素之间有怎样的关系呢?
A
C
B
c
b
a
(1)
三边之间的关系:a
2+b
2=_____;
(2)锐角之间的关系:∠A+∠B=_____;
(3)边角之间的关系:
sinA=
,cosA
=
,tanA
=
.
c
2
90°
合作探究
探究点一
解直角三角形的定义
合作探究
如图,设塔顶中心点为B,
塔身中心线与垂直中心线的夹角为∠A,
过B点向垂直中心线引垂线,垂足为点C.
在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m.
根据以上条件可以求出塔身中心线
与垂直中心线的夹角.
你愿意试着计算一下吗?
合作探究
解:
利用计算器可得
.
将上述问题推广到一般情形,
就是:
已知直角三角形的斜边和一条直角边,
求它的锐角的度数.
合作探究
A
B
C
30
在Rt△ABC
中,
(2)根据AC=
,BC=
你能求出这个三角形的其他元素吗?
(1)根据∠A=
60°,斜边AB=30,
∠B
AC
BC
你能求出这个三角形的其他元素吗?
(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元素吗?
一角一边
两边
不能
两角
你发现了什么?
合作探究
在直角三角形的六个元素中,
除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
合作探究
定义:
在直角三角形中,由已知元素
求出其余未知元素的过程,
叫做解直角三角形.
合作探究
A
B
a
b
c
C
在解直角三角形的过程中,一般
要用到下面一些关系:
(1)三边之间的关系
a2+b2=c2
(勾股定理)
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
合作探究
A
B
a
b
c
C
合作探究
探究点二
解直角三角形
合作探究
例
1
如图,在Rt△ABC
中,∠C=90°,解这个直角三角形.
A
B
C
解:
合作探究
例
2
如图,在Rt△ABC
中,∠B=35°,b=20,
解这个直角三角形(结果保留小数点后一位).
A
B
C
a
b
=
c
20
35°
解:
你还有其他方法求出c
吗?
合作探究
针对训练
如图,从点C
测得树的顶角为33?,BC=20米,
则树高AB=________米(用计算器计算,结果精确到0.1米).
解析:
AB=BC·tanC=20×tan33°=13.0.
答案:
13.0
13.0
课堂小结
1.解直角三角形的关键是找到与已知和未知相关联的直角三角形,
当图形中没有直角三角形时,要通过作辅助线构造直角三角形
(作某边上的高是常用的辅助线).
2.一些解直角三角形的问题往往与其他知识联系,
所以在复习时要形成知识结构,要把解直角三角形作为一种工具,
能在解决各种数学问题时合理运用.
巩固拓展
1.在下列直角三角形中不能求解的是(
)
A.已知一直角边一锐角
B.已知一斜边一锐角
C.已知两边
D.已知两角
D
2.边长为6cm的等边三角形中,其一边上高的长度
为________cm.
解析:
一边上的高=6×sin60°=
(cm).
巩固拓展
3.如图,小明为了测量其所在位置,A点到河对岸B点之间的
距离,沿着与AB垂直的方向走了m米,到达点C,测得∠ACB=α,
那么AB等于(
)
A
B
C
m
A.
m·sinα米
B.m·tanα米
C.m·cosα米
D.
米
B
巩固拓展
4.已知:如图,在Rt△ABC
中,
∠C=90°,AC=
.
点D
为BC
边上一点,
且BD=2AD,∠ADC=60°,
求△ABC
的周长(结果保留根号).
巩固拓展
解析:
要求△ABC
的周长,
只要求得BC
及AB
的长度即可.
根据Rt△ADC
中∠ADC
的正弦值
和AC
的长度,可以求得AD
的长度,
也可求得CD
的长度;
再根据已知条件求得BD
的长度,
继而求得BC
的长度;
运用勾股定理可以求得AB
的长度,
最后求得△ABC
的周长.
巩固拓展
解:
