人教版九年级数学下册 28.2.2 应用举例 第二课时 方向角和坡角在解直角三角形中的应用课件(26张ppt)
文档属性
| 名称 | 人教版九年级数学下册 28.2.2 应用举例 第二课时 方向角和坡角在解直角三角形中的应用课件(26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
28
28.2.2
应用举例
第2课时
方位角和坡角在解直角三角形中的应用
锐角三角函数
学习目标
1.了解“方位角”航海术语,并能根据题意画出示意图.
2.利用解直角三角形的方法解决航海问题中的应用.
导入新课
画出方向图(表示东南西北四个方向的)并依次画出表示东南方向、西北方向、
北偏东65度、南偏东34度
方向的射线.
北
南
西
东
西北
北偏东65度
东南
南偏东34度
合作探究
探究点一
方位角问题
合作探究
例
5
如图,一艘海轮位于灯塔P的北偏东65度方向,
距离灯塔80海里的A处,
它沿正南方向航行一段时间后,
到达位于灯塔P的南偏东34
度方向上的B处.
这时,B处距离灯塔P有多远(结果取整数)?
合作探究
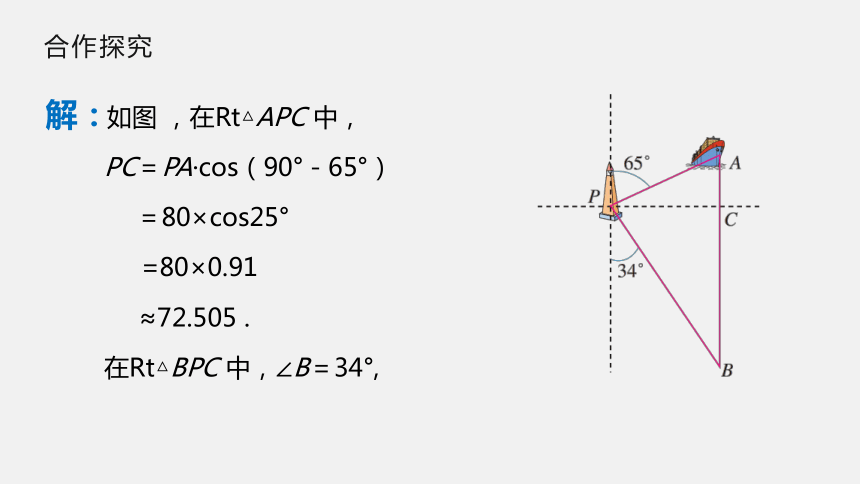
解:
如图
,在Rt△APC
中,
PC=PA·cos(90°-65°)
=80×cos25°
=80×0.91
≈72.505
.
在Rt△BPC
中,∠B=34°,
合作探究
当海轮到达位于灯塔P
的南偏东34°方向时,
它距离灯塔P
大约130海里.
合作探究
小组讨论
1
通过对上面例题的学习,
你对方位角问题的解答有何感想?
进而请你归纳利用解直角三角形的知识解决问题的一般过程.
合作探究
反思小结
方位角是一种表示方向的角,在航海、测绘等位置确定中非常重要.
解决方位角问题,首先明确概念,通过添加辅助线,
把具体问题抽象成直角三角形模型,
利用直角三角形的边角关系以及勾股定理来解题.
合作探究
反思小结
2.利用解直角三角形的知识解决问题的一般过程:
(1)将实际问题抽象为数学问题
(画出平面图形,转化为解直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数等解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
合作探究
针对训练
1.
如图,一艘海轮位于灯塔P的东北方向,
距离灯塔
海里的A处,
它沿正南方向航行一段时间后,
到达位于灯塔P
的南偏东
方向上的B处,
则海轮行驶的路程
AB为多少海里(结果保留根号)?
合作探究
解:
在Rt△APC中,
∵
AP=40
,∠APC=45°
∴
AC=PC=40
在Rt△BPC中,
∵
∠PBC=30°,∴
∠BPC=60°
∴
BC=PC
·
tan60°=40×
=40
∴
AB=AC+BC=40+40
(海里)
答:
海轮行驶的路程
AB为
(40+40
)
海里.
合作探究
探究点二
化整为零,积零为整,
化曲为直,以直代曲的解决问题的策略
合作探究
解直角三角形有广泛的应用,
解决问题时,要根据实际情况灵活运用相关知识,
例如,当我们要测量如图所示大坝的高度h
时,
只要测出仰角a
和大坝的坡面长度l,
就能算出h=lsina,
合作探究
但是,当我们要测量如图所示的山高h
时,问题就不那么简单了,
这是由于不能很方便地得到仰角a
和山坡长度l.
合作探究
坝坡是“直”的,而山坡是“曲”的,
怎样解决这样的问题呢?
与测坝高相比,测山高的困难在于:
合作探究
我们设法“化曲为直,以直代曲”.
我们可以把山坡“化整为零”地
划分为一些小段,图表示其中一部分小段,划分小段时,注意使每一
小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角a1,这样就可以算出这段山坡的高度h1=l1sina1.
合作探究
在每小段上,我们都构造出直角三角形,
利用上面的方法分别算出各段山坡的高度h1,h2,…,hn,
然后我们再“积零为整”,把h1,h2,…,hn相加,
于是得到山高h.
以上解决问题中所用的“化整为零,积零为整”
“化曲为直,以直代曲”的做法,就是高等数学中微积分的基本思想,
它在数学中有重要地位,在今后的学习中,
你会更多地了解这方面的内容.
(1)将实际问题抽象为数学问题(画出平面图形,转化为__________);
(2)根据条件特点,适当选用___________等去解直角三角形;
(3)得到数学问题的答案;
(4)得到___________的答案.
课堂小结
利用解直角三角形的知识解决实际问题的一般过程是:
几何图形
三角函数
实际问题
巩固拓展
1.如下图,在一次数学课外活动中,
测得电线杆底部B与钢缆固定点O
的距离为4米,钢缆与地面的夹角∠BOA为60?,
则这条钢缆在电线杆上的固定点A
到地面的距离AB
是多少米.
(结果保留根号).
巩固拓展
解:
在Rt△ABO中,
∵
tan∠BOA=
=tan60°=
∴
AB=BO?
tan60°=4
×
=4
(米)
答:这条钢缆在电线杆上的固定点
A到地面的距离AB是4
米。
巩固拓展
3.
如图,海岛A的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行,
在点B处测得海岛A位于北偏东60°,航行12海里到达点C处,
又测得海岛A位于北偏东30°,
如果渔船不改变航向继续向东航行.有没有触礁的危险?
解:
如图,过A作AD⊥BC于点C,则AD的长是A到BC的最短距离.
巩固拓展
解:
由勾股定理得
即渔船继续向正东方向行驶,没有触礁的危险.
∵
∠CAC=30°,∠DAB=60°,
∴
∠BAC=60°-30°=30°,∠ABC=90°-60°=30°,
∴
∠ABC=∠BAC,∴
BC=AC=12(海里),
∵
∠CAC=30°,∠ACC=90°,
∴
CD=
AC=6(海里),
巩固拓展
请根据题中所提供的信息计算、分析一下,
工程继续进行下去,是否会穿过学校?
4.如图,在一次暖气管道的铺设工作中,工程是由A点出发沿正西方向进行的,
在A点的南偏西60°的方向上有一所学校,学校占地是以B点为中心方圆100米的圆形,当工程进行了200米时到达C处,
此时B在C的南偏西30°的方向上,
巩固拓展
解:
过点B作BD⊥AD于点D,EA⊥CA于点A,
FC⊥CA于点C,
由题意得∠BAE=60°,∠BCF=30°
∴
∠CAB=30°,
∴
∠DCB=60°,∴
∠DBC=30°,
∴
∠CBA=∠CBD-∠CAB=30°,
∴
∠CAB=∠CBA,∴
AC=CB=200m,
巩固拓展
解:
∴
在Rt△BCD中,BD=BC?sin60°
=200×
(m)
=100
∵
学校是以B为中心方圆100m的圆形,
∵
100
>100
∴
工程若继续进行下去不会穿越学校.
28
28.2.2
应用举例
第2课时
方位角和坡角在解直角三角形中的应用
锐角三角函数
学习目标
1.了解“方位角”航海术语,并能根据题意画出示意图.
2.利用解直角三角形的方法解决航海问题中的应用.
导入新课
画出方向图(表示东南西北四个方向的)并依次画出表示东南方向、西北方向、
北偏东65度、南偏东34度
方向的射线.
北
南
西
东
西北
北偏东65度
东南
南偏东34度
合作探究
探究点一
方位角问题
合作探究
例
5
如图,一艘海轮位于灯塔P的北偏东65度方向,
距离灯塔80海里的A处,
它沿正南方向航行一段时间后,
到达位于灯塔P的南偏东34
度方向上的B处.
这时,B处距离灯塔P有多远(结果取整数)?
合作探究
解:
如图
,在Rt△APC
中,
PC=PA·cos(90°-65°)
=80×cos25°
=80×0.91
≈72.505
.
在Rt△BPC
中,∠B=34°,
合作探究
当海轮到达位于灯塔P
的南偏东34°方向时,
它距离灯塔P
大约130海里.
合作探究
小组讨论
1
通过对上面例题的学习,
你对方位角问题的解答有何感想?
进而请你归纳利用解直角三角形的知识解决问题的一般过程.
合作探究
反思小结
方位角是一种表示方向的角,在航海、测绘等位置确定中非常重要.
解决方位角问题,首先明确概念,通过添加辅助线,
把具体问题抽象成直角三角形模型,
利用直角三角形的边角关系以及勾股定理来解题.
合作探究
反思小结
2.利用解直角三角形的知识解决问题的一般过程:
(1)将实际问题抽象为数学问题
(画出平面图形,转化为解直角三角形的问题);
(2)根据问题中的条件,适当选用锐角三角函数等解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
合作探究
针对训练
1.
如图,一艘海轮位于灯塔P的东北方向,
距离灯塔
海里的A处,
它沿正南方向航行一段时间后,
到达位于灯塔P
的南偏东
方向上的B处,
则海轮行驶的路程
AB为多少海里(结果保留根号)?
合作探究
解:
在Rt△APC中,
∵
AP=40
,∠APC=45°
∴
AC=PC=40
在Rt△BPC中,
∵
∠PBC=30°,∴
∠BPC=60°
∴
BC=PC
·
tan60°=40×
=40
∴
AB=AC+BC=40+40
(海里)
答:
海轮行驶的路程
AB为
(40+40
)
海里.
合作探究
探究点二
化整为零,积零为整,
化曲为直,以直代曲的解决问题的策略
合作探究
解直角三角形有广泛的应用,
解决问题时,要根据实际情况灵活运用相关知识,
例如,当我们要测量如图所示大坝的高度h
时,
只要测出仰角a
和大坝的坡面长度l,
就能算出h=lsina,
合作探究
但是,当我们要测量如图所示的山高h
时,问题就不那么简单了,
这是由于不能很方便地得到仰角a
和山坡长度l.
合作探究
坝坡是“直”的,而山坡是“曲”的,
怎样解决这样的问题呢?
与测坝高相比,测山高的困难在于:
合作探究
我们设法“化曲为直,以直代曲”.
我们可以把山坡“化整为零”地
划分为一些小段,图表示其中一部分小段,划分小段时,注意使每一
小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角a1,这样就可以算出这段山坡的高度h1=l1sina1.
合作探究
在每小段上,我们都构造出直角三角形,
利用上面的方法分别算出各段山坡的高度h1,h2,…,hn,
然后我们再“积零为整”,把h1,h2,…,hn相加,
于是得到山高h.
以上解决问题中所用的“化整为零,积零为整”
“化曲为直,以直代曲”的做法,就是高等数学中微积分的基本思想,
它在数学中有重要地位,在今后的学习中,
你会更多地了解这方面的内容.
(1)将实际问题抽象为数学问题(画出平面图形,转化为__________);
(2)根据条件特点,适当选用___________等去解直角三角形;
(3)得到数学问题的答案;
(4)得到___________的答案.
课堂小结
利用解直角三角形的知识解决实际问题的一般过程是:
几何图形
三角函数
实际问题
巩固拓展
1.如下图,在一次数学课外活动中,
测得电线杆底部B与钢缆固定点O
的距离为4米,钢缆与地面的夹角∠BOA为60?,
则这条钢缆在电线杆上的固定点A
到地面的距离AB
是多少米.
(结果保留根号).
巩固拓展
解:
在Rt△ABO中,
∵
tan∠BOA=
=tan60°=
∴
AB=BO?
tan60°=4
×
=4
(米)
答:这条钢缆在电线杆上的固定点
A到地面的距离AB是4
米。
巩固拓展
3.
如图,海岛A的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行,
在点B处测得海岛A位于北偏东60°,航行12海里到达点C处,
又测得海岛A位于北偏东30°,
如果渔船不改变航向继续向东航行.有没有触礁的危险?
解:
如图,过A作AD⊥BC于点C,则AD的长是A到BC的最短距离.
巩固拓展
解:
由勾股定理得
即渔船继续向正东方向行驶,没有触礁的危险.
∵
∠CAC=30°,∠DAB=60°,
∴
∠BAC=60°-30°=30°,∠ABC=90°-60°=30°,
∴
∠ABC=∠BAC,∴
BC=AC=12(海里),
∵
∠CAC=30°,∠ACC=90°,
∴
CD=
AC=6(海里),
巩固拓展
请根据题中所提供的信息计算、分析一下,
工程继续进行下去,是否会穿过学校?
4.如图,在一次暖气管道的铺设工作中,工程是由A点出发沿正西方向进行的,
在A点的南偏西60°的方向上有一所学校,学校占地是以B点为中心方圆100米的圆形,当工程进行了200米时到达C处,
此时B在C的南偏西30°的方向上,
巩固拓展
解:
过点B作BD⊥AD于点D,EA⊥CA于点A,
FC⊥CA于点C,
由题意得∠BAE=60°,∠BCF=30°
∴
∠CAB=30°,
∴
∠DCB=60°,∴
∠DBC=30°,
∴
∠CBA=∠CBD-∠CAB=30°,
∴
∠CAB=∠CBA,∴
AC=CB=200m,
巩固拓展
解:
∴
在Rt△BCD中,BD=BC?sin60°
=200×
(m)
=100
∵
学校是以B为中心方圆100m的圆形,
∵
100
>100
∴
工程若继续进行下去不会穿越学校.
