人教版九年级数学下册 29.2 三视图课件(60张ppt)
文档属性
| 名称 | 人教版九年级数学下册 29.2 三视图课件(60张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 00:00:00 | ||
图片预览











文档简介
(共60张PPT)
投影与视图
29
29.2
三视图
学习目标
教学分析
1.会从投影的角度理解视图的概念,明确视图与投影的关系.
2.会画简单几何体的三视图.
3.学会根据物体的三视图描述出基本几何体的形状或实物原型.
4.会进行物体的三视图的有关计算.
导入新课
你能指出这些图形
分别从哪个角度
观察得到的吗?
导入新课
看一看
导入新课
“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中
.“
你能说明是什么原因吗?
导入新课
当我们从某一角度观察一个物体时,
所看到的平面图形叫做物体的一个视图.
视图也可以看作物体在某一个角度的光线下的投影,
对于同一物体,如果从不同角度观察,
所得到的视图可能不同.
合作探究
探究点一
三视图的概念及关系
合作探究
下图是同一本书的三个不同的视图.
你能说出这三个视图分别是从哪三个
方向观察这本书时得到的吗?
合作探究
如图,我们用三个互相垂直的平面(例如墙角处的三面墙壁)作为投影面.
其中正对着我们的叫做正面.
下方的平面叫做水平面,
右边的叫做侧面.
对一个物体(例如一个长方体)在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;
在水平面内得到的由上向下观察物体的视图,叫做俯视图;
在侧面内得到的由左向右观察物体的视图,叫做左视图.
合作探究
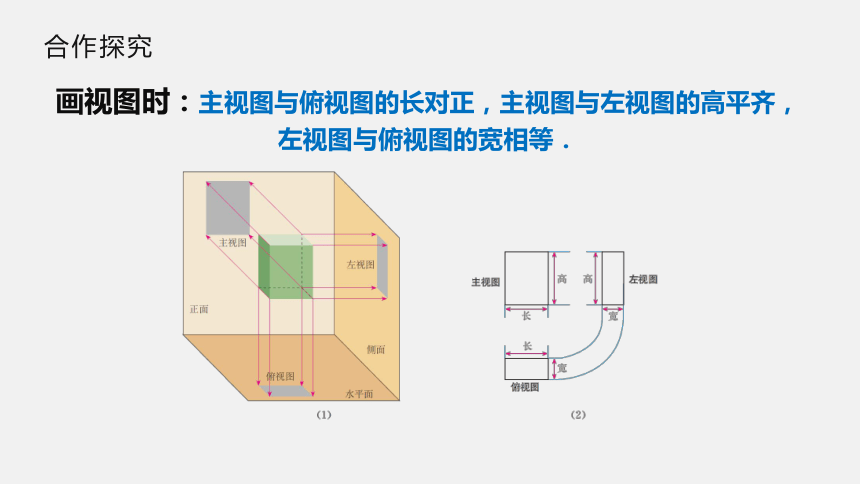
三视图中,主视图与俯视图表示同一物体的长,
主视图与左视图表示同一物体的高,
左视图与俯视图表示同一物体的宽,
因此三个视图的大小是互相联系的,
画三视图时,三个视图要放在正确的位置.
合作探究
画视图时:主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
合作探究
在实际生活中人们经常遇到各种物体,
这些物体的形状虽然经常各不相同,
但是它们一般是由一些基本几何
体(柱体、锥体、球等)组合或切割而成的,
因此会画、会看基本几何体的视图非常必要.
合作探究
针对训练
1
1.一个几何体的主视图、左视图和俯视图是全等图形,
这个几何体可能是(
)
A.圆柱
B.球
C.三棱柱
D.圆锥
B
合作探究
探究点二
三视图的画法
合作探究
活动
1
3.在主视图正右方画出左视图,
注意与主视图“高平齐”,与俯视图“宽相等”.
分析:画这些基本几何体的三视图时,要注意从三个方面观察它们,
具体画法为:
1.确定主视图的位置,画出主视图;
2.在主视图正下方画出俯视图,
注意与主视图“长对正”;
合作探究
合作探究
圆
柱:
主视图
左视图
俯视图
合作探究
三菱柱:
左视图
俯视图
主视图
合作探究
球:
左视图
俯视图
主视图
合作探究
小组讨论
1
如何画三视图,应该注意哪些问题?
合作探究
反思小结
画这些基本几何体的三视图时,要注意从
个方面观察它们.具体画法为:
(1)确定
视图的位置,画出
视图;
(2)在
视图正下方画出
视图,注意与主视图“
”;
(3)在
视图正右方画出
视图.注意与主视图“
”,与俯视图“
”.
三
主
俯
长对正
高平齐
宽相等
左
主
主
主
合作探究
活动
2
画出如图所示的支架(一种小零件)的三视图,
支架的两个台阶的高度和宽度都是同一长度.
1.这个小零件支架是由几个什么基本几何体构成的?
两个大小不等的长方体构成.
2.画组合体的三视图时,构成组合体的各个部分的视图也要注意“
,
,
.”
长对正
高平齐
宽相等
合作探究
3.请你画出它的三视图。
主视图
俯视图
左视图
合作探究
针对训练
2
画出图中的几何体的三视图.
合作探究
合作探究
一个物体的俯视图是圆,
则该物体有可能是
(写两个即可).
圆柱、球
合作探究
前面我们讨论了由立体图形(实物)
画出三视图,
下面我们讨论由三视图想象出立体图形(实物).
合作探究
探究点三
会根据物体的三视图
还原出物体
合作探究
活动
3
根据三视图说出立体图形的名称.
合作探究
分析:
由三视图想象立体图形时,
要先分别根据主视图、俯视图和左视图
想象立体图形的前面、上面和左侧面,
然后再综合起来考虑整体图形.
合作探究
分析
:
(1)
1.从三个方向看立体图形,视图都是矩形,
可以想象出:整体是
,
如图(1)所示;
长方体
2.从正面、侧面看立体图形,
视图都是等腰三角形;从上面看,视图是圆;
可以想象出:整体是
,如图(2)所示.
圆锥
(2)
合作探究
3.根据“长对正,高平齐,
宽相等”的关系,
试下画出它们的立体图形.
合作探究
活动
4
根据物体的三视图,描述物体的形状.
合作探究
2.请同学们再结合左视图与俯视图,试判断下立体图形的名称.
解:
由主视图可知,物体的正面是正五边形;
1.根据主视图判断该物体与什么几何体有关?
解:
由左视图可知,物体的侧面是矩形,且有一条棱;
由俯视图可知,由上向下看物体是矩形,且有一条棱.
所以:物体是五棱柱形状的.
3.若物体为五棱柱,应该是怎样摆放的?
你能根据“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸吗?
合作探究
解:
①
物体是这样摆放的,如图所示.
②可以
合作探究
小组讨论
2
怎样由物体的三视图想象出
原物体的形状?
合作探究
反思小结
由三视图想象立体图形时,
先分别根据主视图、俯视图和左视图
想象立体图形的前面、主面和左侧面的局部形状,
然后再综合起来考虑整体图形.
合作探究
针对训练
3
1.如下图为一个几何体的三视图,
那么这个几何体是____________.
圆
锥
合作探究
2.根据下列物体的三视图,填出几何体的名称:
图1
(1)如图1所示的
几何体是__________
六棱柱
(2)如图1所示的
几何体是_______
圆台
图2
合作探究
探究点四
三视图的有关计算
合作探究
活动
5
某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积.
合作探究
分析
:
1.应先由三视图想象出物体的
;
2.画出物体的
.
密封罐的立体形状
展开图
合作探究
解:
1.先根据给出的三视图确定立体图形,
并确定立体图形的长、宽、高.
三视图为正六棱柱,
它的长、宽、高如图所示;
50cm
50cm
100cm
50cm
合作探究
解:
2.将立体图形展开成一个平面图形(展开图),
观察它的组成部分.
平面展开图:
2个正六边形和6个正方形组成,
如图所示;
合作探究
解:
3.最后根据已知数据,
求出展开图的面积(即所需钢板的面积).
合作探究
反思小结
1.由三视图想象出物体的立体图形;
2.画出物体的平面展开图.
合作探究
针对训练
4
根据几何体的三视图画出它的表面展开图.
(1)这个几何体的名称是
;
合作探究
根据展开图画出物体的三视图,
(2)画出这个几何体的三视图;
圆柱体
三视图
合作探究
(3)求这个几何体的体积和表面积.(π取3.14)
课堂小结
1.画组合体的三视图时,构成组合体的各个部分的视图也要注意“
,
,
.”
长对正
高平齐
宽相等
2.三视图位置有规定,主视图要在左上边,它下方应是
,
左视图坐落在
.
3.画三视图时,三个视图要放在正确的位置,
并且使主视图与俯视图的
,主视图与左视图的
,
左视图与俯视图的
.
俯视图
右上边
长对正
高平齐
宽相等
课堂小结
4.由三视图想象立体图形时,
要先分别根据主视图、俯视图和左视图
想象立体图形的前面、上面和左侧面,
然后再综合起来考虑整体图形.
课堂小结
5.
由三视图求立体图形的面积的方法:
(1)先根据给出的三视图确定立体图形,
并确定立体图形的长、宽、高.
(2)将立体图形展开成一个平面图形(展开图),观察它的组成部分.
(3)最后根据已知数据,求出展开图的面积(即所需钢板的面积).
巩固拓展
1.下图的几何体中,主视图、左视图、俯视图均相同的是(
)
D
巩固拓展
2.一个几何体的三视图形状都相同,大小均等,
那么这个几何体不可能是(
)
A.球
B.三棱锥
C.正方体
D.圆柱
3.将矩形硬纸板绕他的一条边旋转180°所形成的几何体的
主视图和俯视图不可能是(
)
D
A.矩形,矩形
B.半圆、矩形
C.圆、矩形
D.矩形、半圆
C
巩固拓展
4.如图摆放的几何体的俯视图是(
)
B
巩固拓展
5.下图中
①
表示的是组合在一起的模块,那么这个模块的俯视图的是(
)
A.②
B.③
C.④
D.⑤
A
巩固拓展
6.在一仓库里堆放着若干相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来.如图所示,则这堆正方体货箱共有
箱.
9
巩固拓展
7.
如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图.
(1)请写出构成这个几何体的正方体的个数为
;
(2)请根据图中所示的尺寸,计算这个几何体的表面积为
.
5
20
巩固拓展
8.如图,是一个几何体的三视图.
根据图示,可计算出该几何体的侧面积为
.
104π
正
视
图
左
视
图
俯
视
图
8
8
13
巩固拓展
9.如图是某几何体的展开图.
(1)这个几何体的名称是
;
(2)这个几何体的体积为
.
20
10
圆柱体
500π
投影与视图
29
29.2
三视图
学习目标
教学分析
1.会从投影的角度理解视图的概念,明确视图与投影的关系.
2.会画简单几何体的三视图.
3.学会根据物体的三视图描述出基本几何体的形状或实物原型.
4.会进行物体的三视图的有关计算.
导入新课
你能指出这些图形
分别从哪个角度
观察得到的吗?
导入新课
看一看
导入新课
“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中
.“
你能说明是什么原因吗?
导入新课
当我们从某一角度观察一个物体时,
所看到的平面图形叫做物体的一个视图.
视图也可以看作物体在某一个角度的光线下的投影,
对于同一物体,如果从不同角度观察,
所得到的视图可能不同.
合作探究
探究点一
三视图的概念及关系
合作探究
下图是同一本书的三个不同的视图.
你能说出这三个视图分别是从哪三个
方向观察这本书时得到的吗?
合作探究
如图,我们用三个互相垂直的平面(例如墙角处的三面墙壁)作为投影面.
其中正对着我们的叫做正面.
下方的平面叫做水平面,
右边的叫做侧面.
对一个物体(例如一个长方体)在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;
在水平面内得到的由上向下观察物体的视图,叫做俯视图;
在侧面内得到的由左向右观察物体的视图,叫做左视图.
合作探究
三视图中,主视图与俯视图表示同一物体的长,
主视图与左视图表示同一物体的高,
左视图与俯视图表示同一物体的宽,
因此三个视图的大小是互相联系的,
画三视图时,三个视图要放在正确的位置.
合作探究
画视图时:主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
合作探究
在实际生活中人们经常遇到各种物体,
这些物体的形状虽然经常各不相同,
但是它们一般是由一些基本几何
体(柱体、锥体、球等)组合或切割而成的,
因此会画、会看基本几何体的视图非常必要.
合作探究
针对训练
1
1.一个几何体的主视图、左视图和俯视图是全等图形,
这个几何体可能是(
)
A.圆柱
B.球
C.三棱柱
D.圆锥
B
合作探究
探究点二
三视图的画法
合作探究
活动
1
3.在主视图正右方画出左视图,
注意与主视图“高平齐”,与俯视图“宽相等”.
分析:画这些基本几何体的三视图时,要注意从三个方面观察它们,
具体画法为:
1.确定主视图的位置,画出主视图;
2.在主视图正下方画出俯视图,
注意与主视图“长对正”;
合作探究
合作探究
圆
柱:
主视图
左视图
俯视图
合作探究
三菱柱:
左视图
俯视图
主视图
合作探究
球:
左视图
俯视图
主视图
合作探究
小组讨论
1
如何画三视图,应该注意哪些问题?
合作探究
反思小结
画这些基本几何体的三视图时,要注意从
个方面观察它们.具体画法为:
(1)确定
视图的位置,画出
视图;
(2)在
视图正下方画出
视图,注意与主视图“
”;
(3)在
视图正右方画出
视图.注意与主视图“
”,与俯视图“
”.
三
主
俯
长对正
高平齐
宽相等
左
主
主
主
合作探究
活动
2
画出如图所示的支架(一种小零件)的三视图,
支架的两个台阶的高度和宽度都是同一长度.
1.这个小零件支架是由几个什么基本几何体构成的?
两个大小不等的长方体构成.
2.画组合体的三视图时,构成组合体的各个部分的视图也要注意“
,
,
.”
长对正
高平齐
宽相等
合作探究
3.请你画出它的三视图。
主视图
俯视图
左视图
合作探究
针对训练
2
画出图中的几何体的三视图.
合作探究
合作探究
一个物体的俯视图是圆,
则该物体有可能是
(写两个即可).
圆柱、球
合作探究
前面我们讨论了由立体图形(实物)
画出三视图,
下面我们讨论由三视图想象出立体图形(实物).
合作探究
探究点三
会根据物体的三视图
还原出物体
合作探究
活动
3
根据三视图说出立体图形的名称.
合作探究
分析:
由三视图想象立体图形时,
要先分别根据主视图、俯视图和左视图
想象立体图形的前面、上面和左侧面,
然后再综合起来考虑整体图形.
合作探究
分析
:
(1)
1.从三个方向看立体图形,视图都是矩形,
可以想象出:整体是
,
如图(1)所示;
长方体
2.从正面、侧面看立体图形,
视图都是等腰三角形;从上面看,视图是圆;
可以想象出:整体是
,如图(2)所示.
圆锥
(2)
合作探究
3.根据“长对正,高平齐,
宽相等”的关系,
试下画出它们的立体图形.
合作探究
活动
4
根据物体的三视图,描述物体的形状.
合作探究
2.请同学们再结合左视图与俯视图,试判断下立体图形的名称.
解:
由主视图可知,物体的正面是正五边形;
1.根据主视图判断该物体与什么几何体有关?
解:
由左视图可知,物体的侧面是矩形,且有一条棱;
由俯视图可知,由上向下看物体是矩形,且有一条棱.
所以:物体是五棱柱形状的.
3.若物体为五棱柱,应该是怎样摆放的?
你能根据“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸吗?
合作探究
解:
①
物体是这样摆放的,如图所示.
②可以
合作探究
小组讨论
2
怎样由物体的三视图想象出
原物体的形状?
合作探究
反思小结
由三视图想象立体图形时,
先分别根据主视图、俯视图和左视图
想象立体图形的前面、主面和左侧面的局部形状,
然后再综合起来考虑整体图形.
合作探究
针对训练
3
1.如下图为一个几何体的三视图,
那么这个几何体是____________.
圆
锥
合作探究
2.根据下列物体的三视图,填出几何体的名称:
图1
(1)如图1所示的
几何体是__________
六棱柱
(2)如图1所示的
几何体是_______
圆台
图2
合作探究
探究点四
三视图的有关计算
合作探究
活动
5
某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积.
合作探究
分析
:
1.应先由三视图想象出物体的
;
2.画出物体的
.
密封罐的立体形状
展开图
合作探究
解:
1.先根据给出的三视图确定立体图形,
并确定立体图形的长、宽、高.
三视图为正六棱柱,
它的长、宽、高如图所示;
50cm
50cm
100cm
50cm
合作探究
解:
2.将立体图形展开成一个平面图形(展开图),
观察它的组成部分.
平面展开图:
2个正六边形和6个正方形组成,
如图所示;
合作探究
解:
3.最后根据已知数据,
求出展开图的面积(即所需钢板的面积).
合作探究
反思小结
1.由三视图想象出物体的立体图形;
2.画出物体的平面展开图.
合作探究
针对训练
4
根据几何体的三视图画出它的表面展开图.
(1)这个几何体的名称是
;
合作探究
根据展开图画出物体的三视图,
(2)画出这个几何体的三视图;
圆柱体
三视图
合作探究
(3)求这个几何体的体积和表面积.(π取3.14)
课堂小结
1.画组合体的三视图时,构成组合体的各个部分的视图也要注意“
,
,
.”
长对正
高平齐
宽相等
2.三视图位置有规定,主视图要在左上边,它下方应是
,
左视图坐落在
.
3.画三视图时,三个视图要放在正确的位置,
并且使主视图与俯视图的
,主视图与左视图的
,
左视图与俯视图的
.
俯视图
右上边
长对正
高平齐
宽相等
课堂小结
4.由三视图想象立体图形时,
要先分别根据主视图、俯视图和左视图
想象立体图形的前面、上面和左侧面,
然后再综合起来考虑整体图形.
课堂小结
5.
由三视图求立体图形的面积的方法:
(1)先根据给出的三视图确定立体图形,
并确定立体图形的长、宽、高.
(2)将立体图形展开成一个平面图形(展开图),观察它的组成部分.
(3)最后根据已知数据,求出展开图的面积(即所需钢板的面积).
巩固拓展
1.下图的几何体中,主视图、左视图、俯视图均相同的是(
)
D
巩固拓展
2.一个几何体的三视图形状都相同,大小均等,
那么这个几何体不可能是(
)
A.球
B.三棱锥
C.正方体
D.圆柱
3.将矩形硬纸板绕他的一条边旋转180°所形成的几何体的
主视图和俯视图不可能是(
)
D
A.矩形,矩形
B.半圆、矩形
C.圆、矩形
D.矩形、半圆
C
巩固拓展
4.如图摆放的几何体的俯视图是(
)
B
巩固拓展
5.下图中
①
表示的是组合在一起的模块,那么这个模块的俯视图的是(
)
A.②
B.③
C.④
D.⑤
A
巩固拓展
6.在一仓库里堆放着若干相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来.如图所示,则这堆正方体货箱共有
箱.
9
巩固拓展
7.
如图是一个由若干个棱长为1cm的正方体构成的几何体的三视图.
(1)请写出构成这个几何体的正方体的个数为
;
(2)请根据图中所示的尺寸,计算这个几何体的表面积为
.
5
20
巩固拓展
8.如图,是一个几何体的三视图.
根据图示,可计算出该几何体的侧面积为
.
104π
正
视
图
左
视
图
俯
视
图
8
8
13
巩固拓展
9.如图是某几何体的展开图.
(1)这个几何体的名称是
;
(2)这个几何体的体积为
.
20
10
圆柱体
500π
