《流程图》课件6(新人教版A选修1-2)
文档属性
| 名称 | 《流程图》课件6(新人教版A选修1-2) |
|
|
| 格式 | rar | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-20 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
上节课例1:任意给定一个大于1的整数n,试设计一个算法判定n是否为质数.
算法分析:
1.判断n是否等于2,如果n=2,则 n为质数,若n>2,则执行第2步.
2.依次从2到n-1检验是不是n的因数(即是否整除n).若存在这样
的数,则n不是质数,若不存在这样的数,则n为质数.
以上是用自然语言描述一个算法.为了使得算法的描述更为直观和
步骤化,下面介绍另一种描述算法的方法:流程图.
流程图的通俗解释: 由一些图框和有向箭头构成,表示算法按一
定的顺序执行.
上例算法的流程图(见下页)
复习:
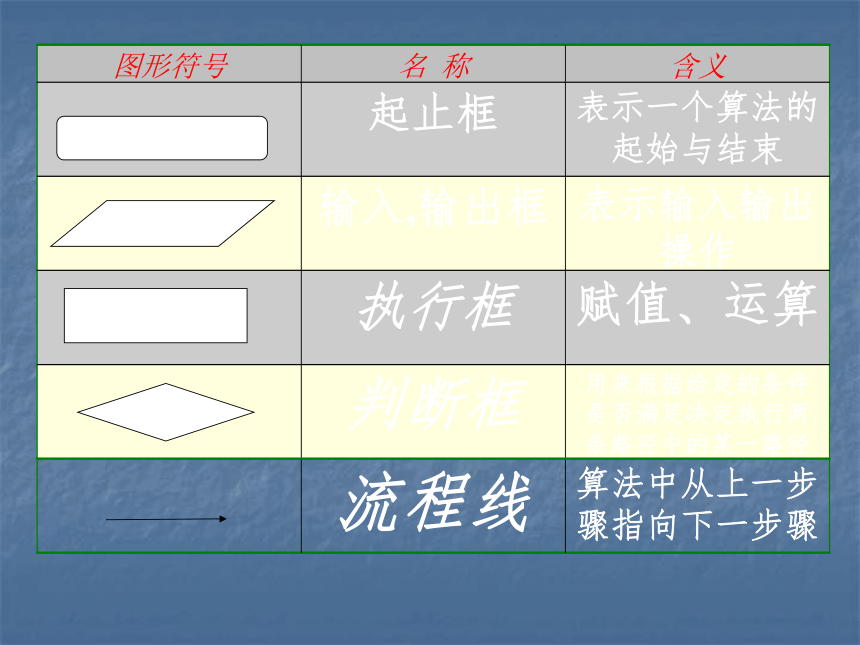
流程图的图形符号:
观察右边的流程图:
(1)有箭头指向的线.
(2)不同形状的框图.
结束
开始
Flag=1
n>2
d=2
输入n
d<=n-1且
flag==1
N不是质数
n是质数
d整除n
Flag=0
Flag==1
d=d+1
是
是
是
否
否
是
否
否
(1)
(2)
否
算法中从上一步骤指向下一步骤
流程线
用来根据给定的条件是否满足决定执行两条路径中的某一路径
判断框
赋值、运算
执行框
表示输入输出操作
输入,输出框
表示一个算法的起始与结束
起止框
含义
名 称
图形符号
2.对程序框 表示的功能描述正确的一项是:…( ).
A.表示算法的起始和结束.
B.表示算法输入和输出的信息.
C.赋值、计算.
D. 按照算法顺序连接程序图框.
1.流程图的功能是:…………………..( ).
表示算法的起始和结束.
表示算法的输入和输出信息.
赋值、运算.
按照算法顺序连接程序图框.
答案:D,B
练习:
Flag=1
输入n
否
d<=n-1且
flag==1
d整除n
Flag=0
d=d+1
是
是
否
(1)
(2)
N不是质数
n是质数
Flag==1
是
否
d=2
否
n>2
是
条件结构
顺序结构
循环结构
算法三种基本逻辑结构
开始
结束
算法三种基本逻辑结构(顺序结构、条件结构、循环结构)
流程图表示,实例,程序演示:
顺序、条件、循环三种基本的逻辑结构:
顺序结构:最简单的算法结构,框与框之间从上到下进行。
任何算法都离不开顺序结构。
A
B
实例:三角形ABC的底BC为4, 高AD为2,求三角形ABC的面积S,
试设计该问题的算法和流程图.
解:算法如下:
1.底BC为a=4, 高AD为b=2.
2.S=1/2ab
3.输出S.
流程图:
开始
a=4,b=2
S=1/2ab
输出S
结束
练习:利用梯形的面积公式计算上底为2,下底为4,高为5
的梯形面积.试设计该问题的算法和流程图.
解:算法如下:
1.a=2, b=4,h=5;
2.S=(a+b) *h/2
3.输出S.
流程图:
开 始
a=2 b=4 h=5
.
输出S.
结 束
程序实现:
main()
{int a,b,h,s;
a=2,b=4,h=5;
s=(a+b)*h/2
printf(“s=%d”,s);
}
输出:15
注:txmz.c
S=(a+b)*h/2
(2).条件结构:一个算法的执行过程中会遇到一些条件的
判断,算法的流程根据条件是否成立有不同的流向.
如图:
P
A
B
是(1)
否(2)
设计求一个数x的绝对值y=
的算法并画出相应的流程图:
练习:
分析:根据绝对值的定义,当x≥0,y=x;当x<0时,y=-x,
所以当给出一个自变量x的值,求它所对应的y值时
必需先判断x的范围,所以要用到条件结构.
解:
算法分析:
输入x.
如果 x≥0,y=x , 否则y=-x..
输出y.
流程图:
程序实现:
main()
{float x,y;
scanf(“%f%f”,&a,&b);
if(x>=0)
y=x;
else
y=-x;
printf(“%f\n”,y);
}
输入:5 -10
输出:5 10 注:jdzhi.c
开始
输入 x
y=x
y=-x
输出y
结束
是
否
x≥0
例:联邦快递公司规定甲、乙两地之间物品的托运费用根据下面的方法计算:
其中f(单位:元)为托运费,ω为托运物品的重量(单位:千克),
试画出计算费用f的程序框图。
自然语言是:
第一步:输入物品重量ω; 第二步:如果ω≦50,那么f=0.53 ω,
否则f=50×0.53+(ω-50) ×0.85; 第三步:输出托运费f.
(3)循环结构:需要重复执行同一操作的结构称为循环结构
.即从某处开始按照一定的条件反复执行某一处理步骤.
反复执行处理的步骤称为循环体.
注:循环结构一定包含条件结构.
实例:1+2+3+4+5+6+7+…..+100=
分析:只需要一个累加变量sum和计数变量i.将累加变量
sum初值赋为0,计数变量i从1到100变化.
算法分析: (见下页)
1. sum=0;
2. i=1;
3. sum=sum+i;
4. i=i+1;
5. 如果i小于等于100,返回重新执行第3步,第4步,第5步,否则结束,得到sum值. sum=1+2+3+4+5+6+........+100.
流程图:
开始
Sum=0
i=i+1
Sum=sum+i
i=1
输出sum
结束
i<=100
第一次循环sum=
第二次循环sum=
第三次循sum=
分析:初值sum=0,i=1
4
0+1=1
,i=2
1+2=3
,i=3
3+3=6
Sum=1
Sum=1+2
Sum=1+2+3
……Sum=1+2+3+…100
是
否
练习: 1+3+5+7+……+31=
分析:只需要一个累加变量sum和计数变量i.将累加
变量sum初值赋为0,计数变量i从1到31变化.
算法分析:(见下页)
开始
Sum=0
i=i+1
Sum=sum+i
i=1
输出sum
结束
i<=100
i<=31
开始
Sum=0
i=1
输出sum
结束
流程图:
Sum=sum+i
算法分析:
(1).sum=0; (2).i=1;
(3).sum=sum+i;(4).i=i+2;
(5).如果i小于等于31,返回重新执行第3步,第4步,第5步,否则结束,得到sum的值,sum=1+3+5+7+……+31.
i=i+2
mian()
{int sum,i;
sum=0;
i=1;
for(i<=31)
{sum=sum+i;
i=i+2;
}
printf(“%d\n”,sum);
} 注:ljia.c
程序实现:
第二次循环sum=
第三次循sum=4+5=9
…..sum=1+3+5+…+31
初值sum=0, i=1
0+1=1
第一次循环sum=
,i=3
1+3=4
,i=5
是
否
任意给定一个大于1的整数n,试设计一个算法判定n是否为质数.并用程序实现。
三种结构的综合应用:
(1) n=5
开始
Flag=1
n>2
d=2
输入n
d<=n-1且
flag=1
N不是质数
n是质数
d整除n
Flag=0
Flag=1
结束
d=d+1
是
是
是
否
否
是
否
否
(1)
(2)
(2)n=4
8
否
程序实现:
main()
{int flag,n,d;
scanf("%d\n",&n);
flag=1;
if(n>2)
for(d=2;d<=n-1&&flag==1;d++)
{if(n%d==0)
flag=0;}
if(flag==1)
{printf("%d",n);
printf(" shi ge su shu\n");}
else
{printf("%d",n);
printf(" bu shi yi ge su shu\n");}
} 注:sushu .c
上节课例1:任意给定一个大于1的整数n,试设计一个算法判定n是否为质数.
算法分析:
1.判断n是否等于2,如果n=2,则 n为质数,若n>2,则执行第2步.
2.依次从2到n-1检验是不是n的因数(即是否整除n).若存在这样
的数,则n不是质数,若不存在这样的数,则n为质数.
以上是用自然语言描述一个算法.为了使得算法的描述更为直观和
步骤化,下面介绍另一种描述算法的方法:流程图.
流程图的通俗解释: 由一些图框和有向箭头构成,表示算法按一
定的顺序执行.
上例算法的流程图(见下页)
复习:
流程图的图形符号:
观察右边的流程图:
(1)有箭头指向的线.
(2)不同形状的框图.
结束
开始
Flag=1
n>2
d=2
输入n
d<=n-1且
flag==1
N不是质数
n是质数
d整除n
Flag=0
Flag==1
d=d+1
是
是
是
否
否
是
否
否
(1)
(2)
否
算法中从上一步骤指向下一步骤
流程线
用来根据给定的条件是否满足决定执行两条路径中的某一路径
判断框
赋值、运算
执行框
表示输入输出操作
输入,输出框
表示一个算法的起始与结束
起止框
含义
名 称
图形符号
2.对程序框 表示的功能描述正确的一项是:…( ).
A.表示算法的起始和结束.
B.表示算法输入和输出的信息.
C.赋值、计算.
D. 按照算法顺序连接程序图框.
1.流程图的功能是:…………………..( ).
表示算法的起始和结束.
表示算法的输入和输出信息.
赋值、运算.
按照算法顺序连接程序图框.
答案:D,B
练习:
Flag=1
输入n
否
d<=n-1且
flag==1
d整除n
Flag=0
d=d+1
是
是
否
(1)
(2)
N不是质数
n是质数
Flag==1
是
否
d=2
否
n>2
是
条件结构
顺序结构
循环结构
算法三种基本逻辑结构
开始
结束
算法三种基本逻辑结构(顺序结构、条件结构、循环结构)
流程图表示,实例,程序演示:
顺序、条件、循环三种基本的逻辑结构:
顺序结构:最简单的算法结构,框与框之间从上到下进行。
任何算法都离不开顺序结构。
A
B
实例:三角形ABC的底BC为4, 高AD为2,求三角形ABC的面积S,
试设计该问题的算法和流程图.
解:算法如下:
1.底BC为a=4, 高AD为b=2.
2.S=1/2ab
3.输出S.
流程图:
开始
a=4,b=2
S=1/2ab
输出S
结束
练习:利用梯形的面积公式计算上底为2,下底为4,高为5
的梯形面积.试设计该问题的算法和流程图.
解:算法如下:
1.a=2, b=4,h=5;
2.S=(a+b) *h/2
3.输出S.
流程图:
开 始
a=2 b=4 h=5
.
输出S.
结 束
程序实现:
main()
{int a,b,h,s;
a=2,b=4,h=5;
s=(a+b)*h/2
printf(“s=%d”,s);
}
输出:15
注:txmz.c
S=(a+b)*h/2
(2).条件结构:一个算法的执行过程中会遇到一些条件的
判断,算法的流程根据条件是否成立有不同的流向.
如图:
P
A
B
是(1)
否(2)
设计求一个数x的绝对值y=
的算法并画出相应的流程图:
练习:
分析:根据绝对值的定义,当x≥0,y=x;当x<0时,y=-x,
所以当给出一个自变量x的值,求它所对应的y值时
必需先判断x的范围,所以要用到条件结构.
解:
算法分析:
输入x.
如果 x≥0,y=x , 否则y=-x..
输出y.
流程图:
程序实现:
main()
{float x,y;
scanf(“%f%f”,&a,&b);
if(x>=0)
y=x;
else
y=-x;
printf(“%f\n”,y);
}
输入:5 -10
输出:5 10 注:jdzhi.c
开始
输入 x
y=x
y=-x
输出y
结束
是
否
x≥0
例:联邦快递公司规定甲、乙两地之间物品的托运费用根据下面的方法计算:
其中f(单位:元)为托运费,ω为托运物品的重量(单位:千克),
试画出计算费用f的程序框图。
自然语言是:
第一步:输入物品重量ω; 第二步:如果ω≦50,那么f=0.53 ω,
否则f=50×0.53+(ω-50) ×0.85; 第三步:输出托运费f.
(3)循环结构:需要重复执行同一操作的结构称为循环结构
.即从某处开始按照一定的条件反复执行某一处理步骤.
反复执行处理的步骤称为循环体.
注:循环结构一定包含条件结构.
实例:1+2+3+4+5+6+7+…..+100=
分析:只需要一个累加变量sum和计数变量i.将累加变量
sum初值赋为0,计数变量i从1到100变化.
算法分析: (见下页)
1. sum=0;
2. i=1;
3. sum=sum+i;
4. i=i+1;
5. 如果i小于等于100,返回重新执行第3步,第4步,第5步,否则结束,得到sum值. sum=1+2+3+4+5+6+........+100.
流程图:
开始
Sum=0
i=i+1
Sum=sum+i
i=1
输出sum
结束
i<=100
第一次循环sum=
第二次循环sum=
第三次循sum=
分析:初值sum=0,i=1
4
0+1=1
,i=2
1+2=3
,i=3
3+3=6
Sum=1
Sum=1+2
Sum=1+2+3
……Sum=1+2+3+…100
是
否
练习: 1+3+5+7+……+31=
分析:只需要一个累加变量sum和计数变量i.将累加
变量sum初值赋为0,计数变量i从1到31变化.
算法分析:(见下页)
开始
Sum=0
i=i+1
Sum=sum+i
i=1
输出sum
结束
i<=100
i<=31
开始
Sum=0
i=1
输出sum
结束
流程图:
Sum=sum+i
算法分析:
(1).sum=0; (2).i=1;
(3).sum=sum+i;(4).i=i+2;
(5).如果i小于等于31,返回重新执行第3步,第4步,第5步,否则结束,得到sum的值,sum=1+3+5+7+……+31.
i=i+2
mian()
{int sum,i;
sum=0;
i=1;
for(i<=31)
{sum=sum+i;
i=i+2;
}
printf(“%d\n”,sum);
} 注:ljia.c
程序实现:
第二次循环sum=
第三次循sum=4+5=9
…..sum=1+3+5+…+31
初值sum=0, i=1
0+1=1
第一次循环sum=
,i=3
1+3=4
,i=5
是
否
任意给定一个大于1的整数n,试设计一个算法判定n是否为质数.并用程序实现。
三种结构的综合应用:
(1) n=5
开始
Flag=1
n>2
d=2
输入n
d<=n-1且
flag=1
N不是质数
n是质数
d整除n
Flag=0
Flag=1
结束
d=d+1
是
是
是
否
否
是
否
否
(1)
(2)
(2)n=4
8
否
程序实现:
main()
{int flag,n,d;
scanf("%d\n",&n);
flag=1;
if(n>2)
for(d=2;d<=n-1&&flag==1;d++)
{if(n%d==0)
flag=0;}
if(flag==1)
{printf("%d",n);
printf(" shi ge su shu\n");}
else
{printf("%d",n);
printf(" bu shi yi ge su shu\n");}
} 注:sushu .c
