六年级下册数学课件-4.4《反比例》北师大版
文档属性
| 名称 | 六年级下册数学课件-4.4《反比例》北师大版 |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-23 18:53:41 | ||
图片预览






文档简介
(共22张PPT)
北师大版六年级数学下册
篱笆镇中心小学宋亚荣
教学目标:
1.结合“长方形相邻两边的边长,路程,时间与速度”等情景经历反比例意义建构的过程,能从变化中看到“不变”,认识反比例。
2.经历比较,分析,归纳等数学活动,提高分析比较,归纳概括能力,初步体会函数思想。
1.什么是成正比例的量?
2.
怎样判定两个量是否成正比例?
这两个量成正比例吗?
(1)速度一定,路程与时间。
(2)征订同一种刊物,征订数量和总价。
(3)一个人的年龄和体重。
1
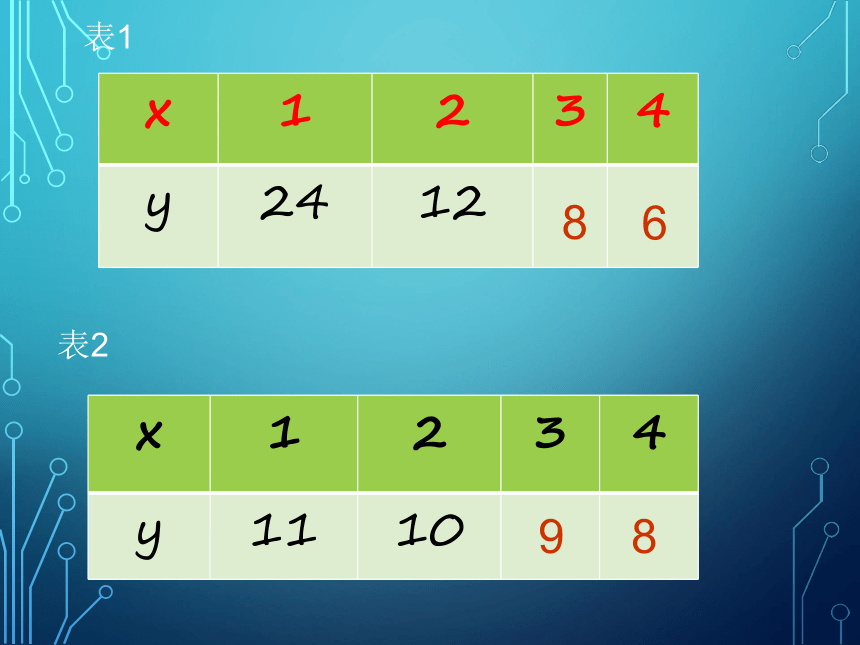
.用X,y表示长方形相邻两边的边长,表(1)是面积为24平方厘米的长方形相邻两边边长的变化关系,表(2)是周长是24厘米的长方形相邻两边边长的变化关系。请把表格填写完整,并说说你分别发现了什么。(单位:cm)
表1
表2
8
9
8
6
x
1
2
3
4
y
24
12
x
1
2
3
4
y
11
10
表1中相邻两边边长的积相等,表2中相邻两边边长的和相等。
表1和表2中,长方形相邻两边边长之间的变化规律相同吗?
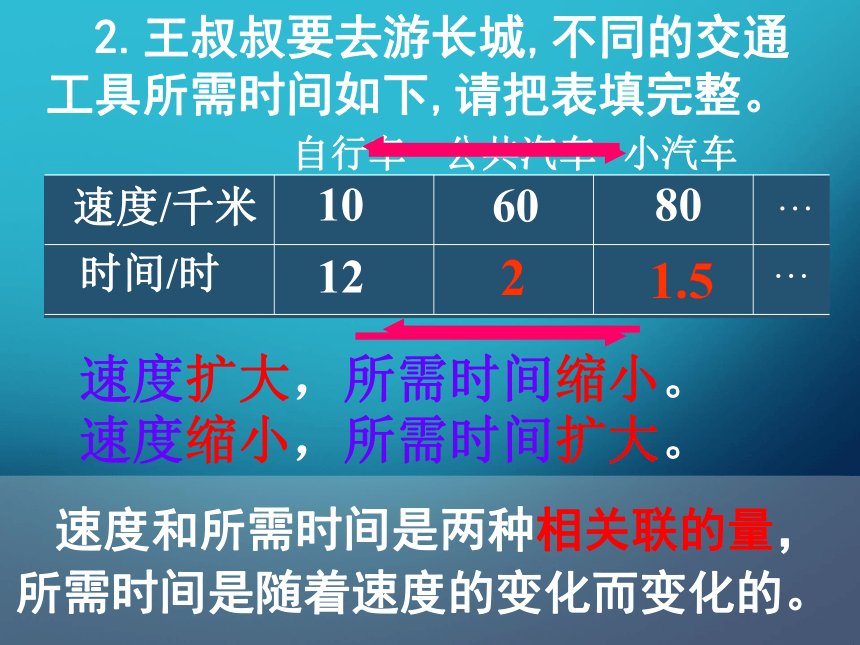
2.王叔叔要去游长城,不同的交通工具所需时间如下,请把表填完整。
时间/时
10
60
80
12
2
1.5
…
…
速度/千米
自行车
公共汽车
小汽车
速度扩大,所需时间缩小。
速度缩小,所需时间扩大。
速度和所需时间是两种相关联的量,所需时间是随着速度的变化而变化的。
80×1.5=120
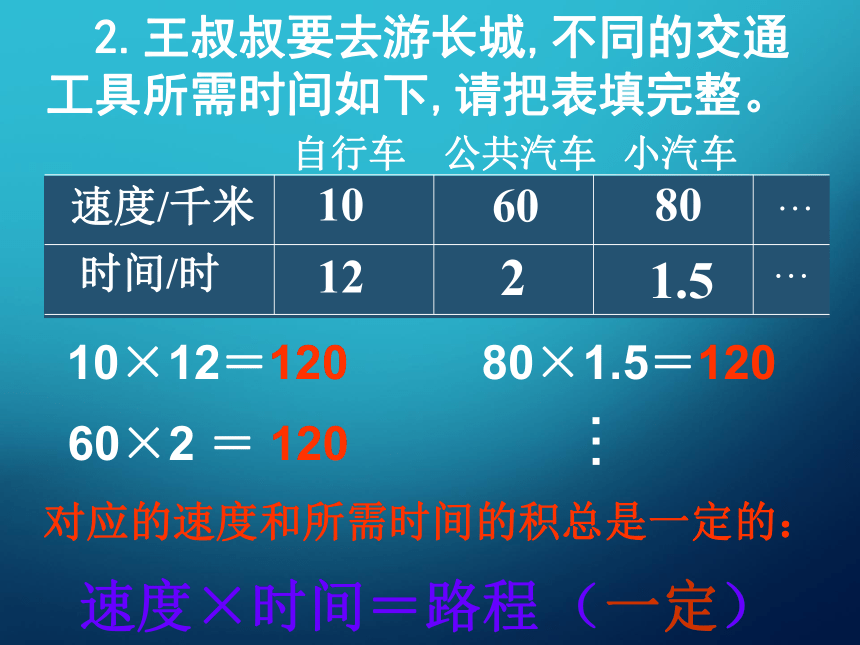
2.王叔叔要去游长城,不同的交通工具所需时间如下,请把表填完整。
时间/时
10
60
80
12
2
1.5
…
…
速度/千米
自行车
公共汽车
小汽车
10×12=120
60×2
=
120
(一定)
速度×时间=路程
对应的速度和所需时间的积总是一定的:
3.有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
150
200
300
(2)分的杯数是怎样随着每杯的果
汁量变化的?
(1)表中有哪两种量?
(3)变化过程中,什么不变?
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
150
200
300
果汁总量不变,也就是对应的每杯果汁量和分的杯数的积相等。
每杯果汁量×分的杯数=果汁总量(一定)
速度×时间=路程(一定)
每杯的果汁量×杯数=果汁总量(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用x和y表示两种相关联的量,用k表示它们的乘积,那么上面这种数量关系式可以怎样写呢??
=
k
(一定)
x和y叫做成反比例的量,它们的关系叫做成反比例的关系?。
判断两种量是否成反比
例的关键是什么?
判定两个量是不是成反比例,关键是看它们的积是不是一定。
买苹果的总钱数一定,苹果的单价与数量成反比例吗?你是怎么想的?与同伴交流。
张伯伯骑自行车从家
到县城,骑自行车的速
度和所需的时间。
判断下面的两种量是不是成反比例,并说明理由。
因为速度×时间=路程(一定),所以骑自行车的速度和所需的时间成反比例。
骑车的速度和所需时间成反比例。
奇思读一本书,已读的页数与剩下的页数的情况如下。
已读的页数与剩下的页数成反比例吗?为什么?
请举一个成反比例的例子,并与同伴交流。
已读的页数
1
2
3
4
5
6
剩下的页数
79
78
77
76
75
74
课堂检测
想一想,填一填。
1.两种相关联的量,一种量变化,另一种量也随着(
),两种量中相对应的两个数的积一定,这两种量叫做(
)
它们的关系叫作(
)。
变化
反比例关系
反比例的量
课堂检测
想一想,填一填。
2.如果xy=
k(一定),那么x和y之间的关系是(
)关系。
反比例
课堂检测
想一想,填一填。
3.小明做12道数学题,做完的题和没做完的题(
)比例。
不成
这节课学习的是什么内容?
1.反比例的意义是什么?
2.判断两种量是不是成反比例,关键是什么?
谢谢
北师大版六年级数学下册
篱笆镇中心小学宋亚荣
教学目标:
1.结合“长方形相邻两边的边长,路程,时间与速度”等情景经历反比例意义建构的过程,能从变化中看到“不变”,认识反比例。
2.经历比较,分析,归纳等数学活动,提高分析比较,归纳概括能力,初步体会函数思想。
1.什么是成正比例的量?
2.
怎样判定两个量是否成正比例?
这两个量成正比例吗?
(1)速度一定,路程与时间。
(2)征订同一种刊物,征订数量和总价。
(3)一个人的年龄和体重。
1
.用X,y表示长方形相邻两边的边长,表(1)是面积为24平方厘米的长方形相邻两边边长的变化关系,表(2)是周长是24厘米的长方形相邻两边边长的变化关系。请把表格填写完整,并说说你分别发现了什么。(单位:cm)
表1
表2
8
9
8
6
x
1
2
3
4
y
24
12
x
1
2
3
4
y
11
10
表1中相邻两边边长的积相等,表2中相邻两边边长的和相等。
表1和表2中,长方形相邻两边边长之间的变化规律相同吗?
2.王叔叔要去游长城,不同的交通工具所需时间如下,请把表填完整。
时间/时
10
60
80
12
2
1.5
…
…
速度/千米
自行车
公共汽车
小汽车
速度扩大,所需时间缩小。
速度缩小,所需时间扩大。
速度和所需时间是两种相关联的量,所需时间是随着速度的变化而变化的。
80×1.5=120
2.王叔叔要去游长城,不同的交通工具所需时间如下,请把表填完整。
时间/时
10
60
80
12
2
1.5
…
…
速度/千米
自行车
公共汽车
小汽车
10×12=120
60×2
=
120
(一定)
速度×时间=路程
对应的速度和所需时间的积总是一定的:
3.有600毫升果汁,可平均分成若干杯。请把下表填完整
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
150
200
300
(2)分的杯数是怎样随着每杯的果
汁量变化的?
(1)表中有哪两种量?
(3)变化过程中,什么不变?
分的杯数/杯
每杯的果汁量/ml
6
5
4
3
2
100
…
…
120
150
200
300
果汁总量不变,也就是对应的每杯果汁量和分的杯数的积相等。
每杯果汁量×分的杯数=果汁总量(一定)
速度×时间=路程(一定)
每杯的果汁量×杯数=果汁总量(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用x和y表示两种相关联的量,用k表示它们的乘积,那么上面这种数量关系式可以怎样写呢??
=
k
(一定)
x和y叫做成反比例的量,它们的关系叫做成反比例的关系?。
判断两种量是否成反比
例的关键是什么?
判定两个量是不是成反比例,关键是看它们的积是不是一定。
买苹果的总钱数一定,苹果的单价与数量成反比例吗?你是怎么想的?与同伴交流。
张伯伯骑自行车从家
到县城,骑自行车的速
度和所需的时间。
判断下面的两种量是不是成反比例,并说明理由。
因为速度×时间=路程(一定),所以骑自行车的速度和所需的时间成反比例。
骑车的速度和所需时间成反比例。
奇思读一本书,已读的页数与剩下的页数的情况如下。
已读的页数与剩下的页数成反比例吗?为什么?
请举一个成反比例的例子,并与同伴交流。
已读的页数
1
2
3
4
5
6
剩下的页数
79
78
77
76
75
74
课堂检测
想一想,填一填。
1.两种相关联的量,一种量变化,另一种量也随着(
),两种量中相对应的两个数的积一定,这两种量叫做(
)
它们的关系叫作(
)。
变化
反比例关系
反比例的量
课堂检测
想一想,填一填。
2.如果xy=
k(一定),那么x和y之间的关系是(
)关系。
反比例
课堂检测
想一想,填一填。
3.小明做12道数学题,做完的题和没做完的题(
)比例。
不成
这节课学习的是什么内容?
1.反比例的意义是什么?
2.判断两种量是不是成反比例,关键是什么?
谢谢
