19.2.3 正方形(1)(含答案)
文档属性
| 名称 | 19.2.3 正方形(1)(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 45.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-20 12:43:49 | ||
图片预览

文档简介
19.2.3 正方形(1)
◆回顾归纳
1.正方形的四个角是_____角,四条边_____,对角线_______________________.
2.正方形是______对称图形,它有______条对称轴.
3.若正方形边长为a,则对角线长为___________,面积为__________.
◆课堂测控
测试点 正方形的性质
1.正方形的面积为4,则它的边长为____,对角线长为_____.
2.已知正方形ABCD对角线AC,BD相交于点O,且AC=16cm,则DO=_____cm,BO=____cm,∠OCD=____度.
3.矩形,菱形,正方形都具有的性质是( )
A.对角线相等 B.对角线垂直平分
C.对角线平分一组对角 D.对角线互相垂直
4.正方形具有而菱形不一定具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.对角线平分一组对角
5.(合作研讨题)如图所示,正方形ABCD的对角线AC,BD相交于O.
(1)图中有哪些线段相等?
(2)图中有哪些角相等?
(3)图中有哪些等腰三角形?
(4)图中有哪些三角形是全等的?
◆课后测控
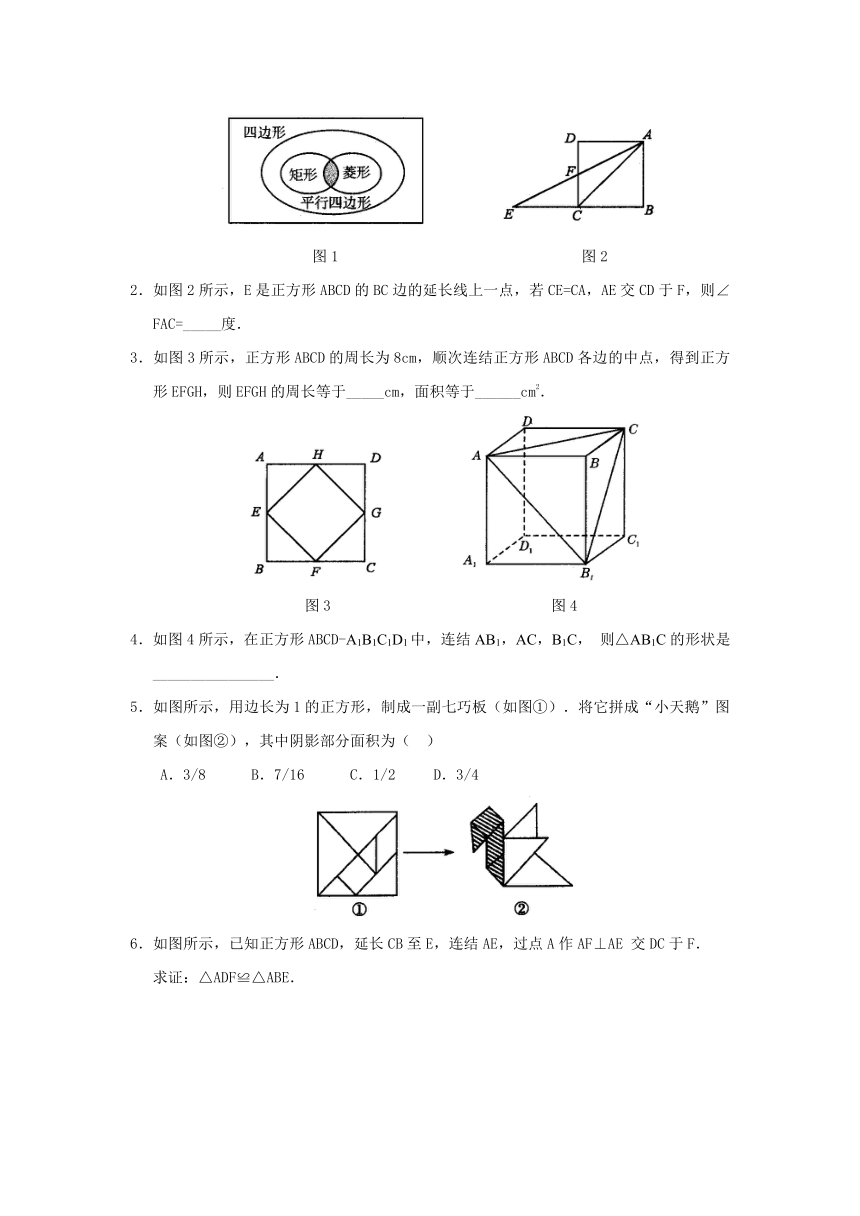
1.如图1所示,阴影部分表示的四边形是_______.
图1 图2
2.如图2所示,E是正方形ABCD的BC边的延长线上一点,若CE=CA,AE交CD于F,则∠FAC=_____度.
3.如图3所示,正方形ABCD的周长为8cm,顺次连结正方形ABCD各边的中点,得到正方形EFGH,则EFGH的周长等于_____cm,面积等于______cm2.
图3 图4
4.如图4所示,在正方形ABCD-A1B1C1D1中,连结AB1,AC,B1C,则△AB1C的形状是________________.
5.如图所示,用边长为1的正方形,制成一副七巧板(如图①).将它拼成“小天鹅”图案(如图②),其中阴影部分面积为( )
A.3/8 B.7/16 C.1/2 D.3/4
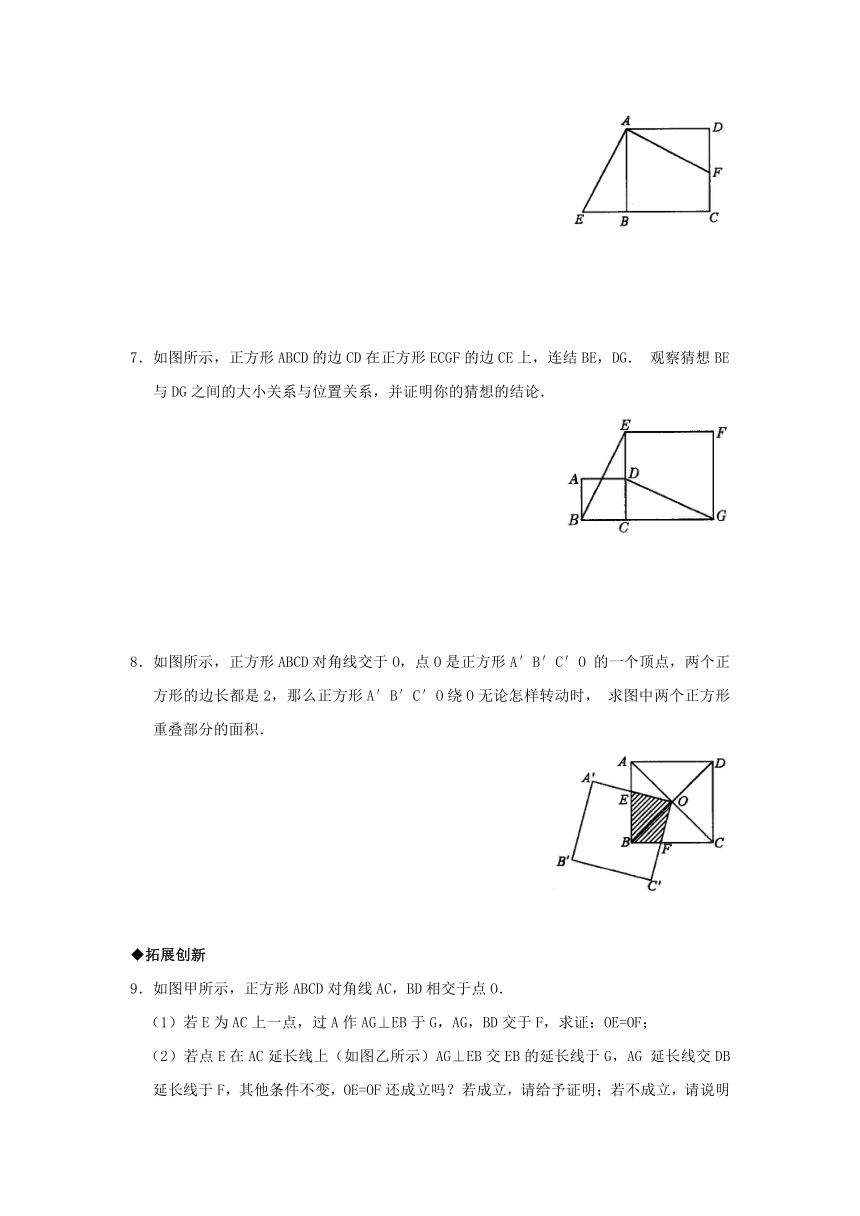
6.如图所示,已知正方形ABCD,延长CB至E,连结AE,过点A作AF⊥AE交DC于F.
求证:△ADF≌△ABE.
7.如图所示,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE,DG.观察猜想BE与DG之间的大小关系与位置关系,并证明你的猜想的结论.
8.如图所示,正方形ABCD对角线交于O,点O是正方形A′B′C′O的一个顶点,两个正方形的边长都是2,那么正方形A′B′C′O绕O无论怎样转动时,求图中两个正方形重叠部分的面积.
( http: / / )
◆拓展创新
9.如图甲所示,正方形ABCD对角线AC,BD相交于点O.
(1)若E为AC上一点,过A作AG⊥EB于G,AG,BD交于F,求证:OE=OF;
(2)若点E在AC延长线上(如图乙所示)AG⊥EB交EB的延长线于G,AG延长线交DB延长线于F,其他条件不变,OE=OF还成立吗?若成立,请给予证明;若不成立,请说明理由.
答案:
回顾归纳
1.直,都相等,垂直平分且相等并且每条对角线平分一组对角
2.轴,4 3.a,a2
课堂测控
1.2,2 2.8,8,45° 3.B 4.B
5.(1)AB=BC=CD=DA,AC=BD,OA=OB=OC=OD
(2)∠BAD=∠ADC=∠BCD=∠ABC
∠BAC=∠BAD=∠DBC=∠ACB=∠ACD=∠BDC=∠ADB=∠DAC
(3)△AOB △BOC △COD △AOD △ABC △BCD △ACD △ABD
(4)△AOB≌△BOC≌△COD≌△AOD
△ABC≌△BCD≌△ACD≌ABD
课后测控
1.正方形
2.22.5 点拨:利用∠ACB=45°求解.
3.4,2 4.等边三角形 5.A
6.∵正方形ABCD,∴∠BAD=∠DAF+∠BAF=90°.
又∵AF⊥AE,∴∠EAB+∠BAF=90°.
∴∠DAF=∠EAB.
又∵正方形ABCD,
∴∠ABE=∠D=90°,AB=AD.
∴△ADF≌△ABE.
7.∵四边形ABCD和四边形ECGF是正方形,
∴BC=CD,CE=CG,∠BCE=∠DCG=90°,
∴△BCE≌△DCG,∴BE=DG.
8.∵ABCD和A′B′C′O都是边长为2的正方形,
∴OA=OB,∠AOB=∠A′OC′=90°.
∠BAO=∠OBC=45°,∴∠AOB-∠BOE=∠A′OC′-∠BOE,即∠AOE=∠BOF.
∴△AOE≌△BOF,∴重叠部分面积为:
S△BOE+S△BOF =S△BOE +S△AOE =S△AOB =S正方形ABCD=×22=1.
拓展创新
9.(1)∵四边形ABCD为正方形,
∴∠BOE=∠AOF=90°,BO=AO.
又∵AG⊥BE,∴∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2,∴Rt△BOE≌Rt△AOF.
∴OE=OF.
(2)上述结论OE=OF仍成立.
∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,BO=AO.
又∵AG⊥EB,∴∠OEB+∠EAF=90°,
∠OFA=∠FAE=90°,∴∠OEB=∠OFA,
∴Rt△BOE≌Rt△AOF,∴OE=OF.
◆回顾归纳
1.正方形的四个角是_____角,四条边_____,对角线_______________________.
2.正方形是______对称图形,它有______条对称轴.
3.若正方形边长为a,则对角线长为___________,面积为__________.
◆课堂测控
测试点 正方形的性质
1.正方形的面积为4,则它的边长为____,对角线长为_____.
2.已知正方形ABCD对角线AC,BD相交于点O,且AC=16cm,则DO=_____cm,BO=____cm,∠OCD=____度.
3.矩形,菱形,正方形都具有的性质是( )
A.对角线相等 B.对角线垂直平分
C.对角线平分一组对角 D.对角线互相垂直
4.正方形具有而菱形不一定具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.对角线平分一组对角
5.(合作研讨题)如图所示,正方形ABCD的对角线AC,BD相交于O.
(1)图中有哪些线段相等?
(2)图中有哪些角相等?
(3)图中有哪些等腰三角形?
(4)图中有哪些三角形是全等的?
◆课后测控
1.如图1所示,阴影部分表示的四边形是_______.
图1 图2
2.如图2所示,E是正方形ABCD的BC边的延长线上一点,若CE=CA,AE交CD于F,则∠FAC=_____度.
3.如图3所示,正方形ABCD的周长为8cm,顺次连结正方形ABCD各边的中点,得到正方形EFGH,则EFGH的周长等于_____cm,面积等于______cm2.
图3 图4
4.如图4所示,在正方形ABCD-A1B1C1D1中,连结AB1,AC,B1C,则△AB1C的形状是________________.
5.如图所示,用边长为1的正方形,制成一副七巧板(如图①).将它拼成“小天鹅”图案(如图②),其中阴影部分面积为( )
A.3/8 B.7/16 C.1/2 D.3/4
6.如图所示,已知正方形ABCD,延长CB至E,连结AE,过点A作AF⊥AE交DC于F.
求证:△ADF≌△ABE.
7.如图所示,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE,DG.观察猜想BE与DG之间的大小关系与位置关系,并证明你的猜想的结论.
8.如图所示,正方形ABCD对角线交于O,点O是正方形A′B′C′O的一个顶点,两个正方形的边长都是2,那么正方形A′B′C′O绕O无论怎样转动时,求图中两个正方形重叠部分的面积.
( http: / / )
◆拓展创新
9.如图甲所示,正方形ABCD对角线AC,BD相交于点O.
(1)若E为AC上一点,过A作AG⊥EB于G,AG,BD交于F,求证:OE=OF;
(2)若点E在AC延长线上(如图乙所示)AG⊥EB交EB的延长线于G,AG延长线交DB延长线于F,其他条件不变,OE=OF还成立吗?若成立,请给予证明;若不成立,请说明理由.
答案:
回顾归纳
1.直,都相等,垂直平分且相等并且每条对角线平分一组对角
2.轴,4 3.a,a2
课堂测控
1.2,2 2.8,8,45° 3.B 4.B
5.(1)AB=BC=CD=DA,AC=BD,OA=OB=OC=OD
(2)∠BAD=∠ADC=∠BCD=∠ABC
∠BAC=∠BAD=∠DBC=∠ACB=∠ACD=∠BDC=∠ADB=∠DAC
(3)△AOB △BOC △COD △AOD △ABC △BCD △ACD △ABD
(4)△AOB≌△BOC≌△COD≌△AOD
△ABC≌△BCD≌△ACD≌ABD
课后测控
1.正方形
2.22.5 点拨:利用∠ACB=45°求解.
3.4,2 4.等边三角形 5.A
6.∵正方形ABCD,∴∠BAD=∠DAF+∠BAF=90°.
又∵AF⊥AE,∴∠EAB+∠BAF=90°.
∴∠DAF=∠EAB.
又∵正方形ABCD,
∴∠ABE=∠D=90°,AB=AD.
∴△ADF≌△ABE.
7.∵四边形ABCD和四边形ECGF是正方形,
∴BC=CD,CE=CG,∠BCE=∠DCG=90°,
∴△BCE≌△DCG,∴BE=DG.
8.∵ABCD和A′B′C′O都是边长为2的正方形,
∴OA=OB,∠AOB=∠A′OC′=90°.
∠BAO=∠OBC=45°,∴∠AOB-∠BOE=∠A′OC′-∠BOE,即∠AOE=∠BOF.
∴△AOE≌△BOF,∴重叠部分面积为:
S△BOE+S△BOF =S△BOE +S△AOE =S△AOB =S正方形ABCD=×22=1.
拓展创新
9.(1)∵四边形ABCD为正方形,
∴∠BOE=∠AOF=90°,BO=AO.
又∵AG⊥BE,∴∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2,∴Rt△BOE≌Rt△AOF.
∴OE=OF.
(2)上述结论OE=OF仍成立.
∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,BO=AO.
又∵AG⊥EB,∴∠OEB+∠EAF=90°,
∠OFA=∠FAE=90°,∴∠OEB=∠OFA,
∴Rt△BOE≌Rt△AOF,∴OE=OF.
