1.4.2正弦函数,余弦函数的性质(二)
文档属性
| 名称 | 1.4.2正弦函数,余弦函数的性质(二) |

|
|
| 格式 | rar | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-20 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
( 2 ,0)
( ,-1)
( ,0)
( ,1)
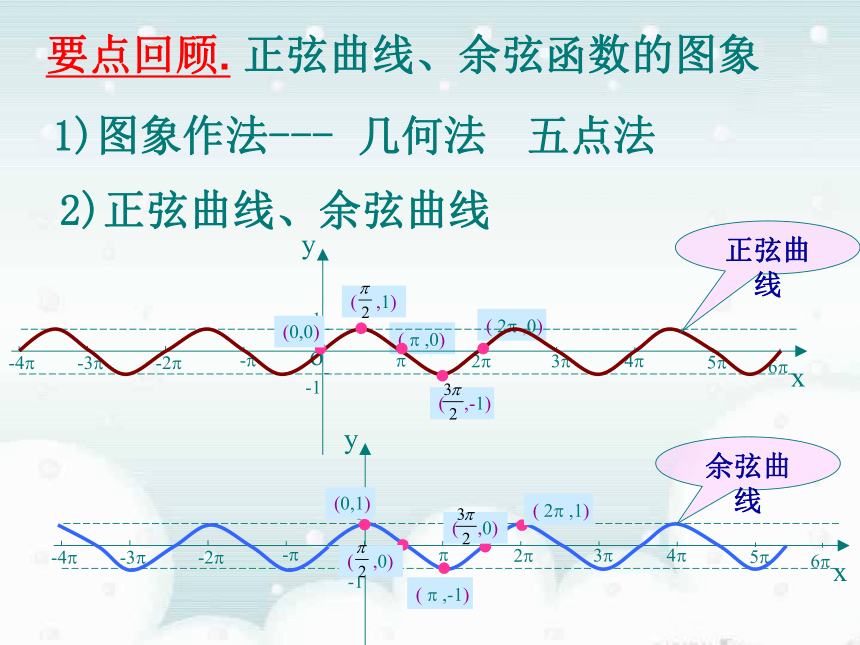
要点回顾.
正弦曲线、余弦函数的图象
1)图象作法---
几何法
五点法
2)正弦曲线、余弦曲线
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦曲线
(0,1)
( ,0)
( ,-1)
( ,0)
( 2 ,1)
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦曲线
(0,0)
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
x
y
1
-1
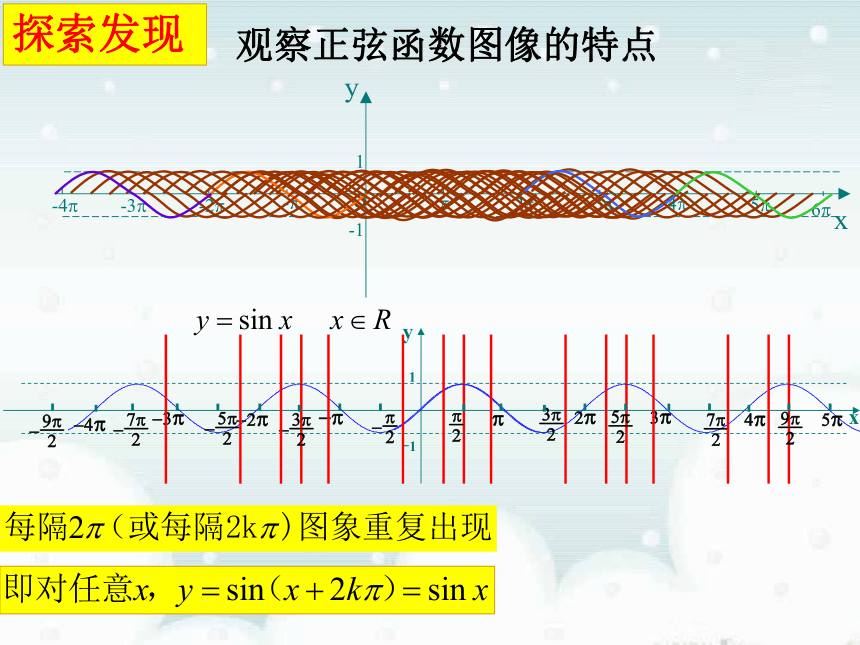
探索发现
观察正弦函数图像的特点
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
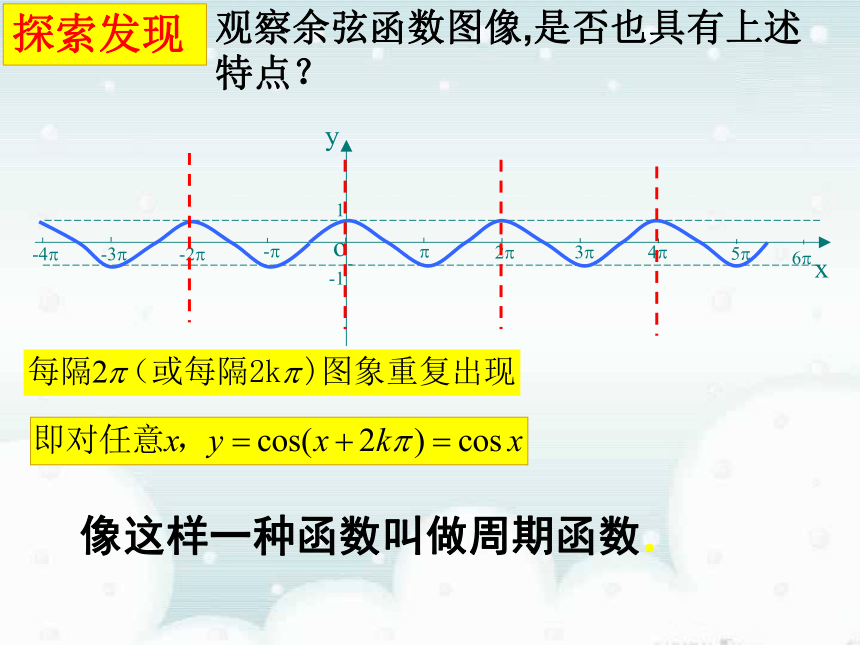
探索发现
观察余弦函数图像,是否也具有上述特点?
像这样一种函数叫做周期函数.
周期函数的定义:对于函数 f(x), 如果
存在一个非零常数T,使得当 x 取定义域
内的每一个值时,都有 f (x+T)= f(x),那么
函数 f(x) 就叫做周期函数,非零常数T叫
做这个函数的周期 .
注意:
1°周期函数x∈定义域M,则必
有 x +T∈M.
2°对“每一个值”的理解:只要有一个
反例, 则 f (x)就不为周期函数.
3°T往往是多值的(如 y = sinx 2π, 4π,
…, -2π, -4π, …都是周期)周期T中最
小正数叫做 f (x)的最小正周期 (有些周
期函数没有最小正周期) .
本书中涉及的周期,如果不加特别说明,一般都是指函数的最小正周期
周期概念的拓展
1 函数f(x)=sinx(x≥0)是否为周期函数?函数f(x)=sinx(x≤0)是否为周期函数?
2 函数f(x)=sinx(x>0)是否为周期函数?函数f(x)=sinx(x≠3kπ)是否为周期函数?
3 函数f(x)=sinx,x∈[0,10π]是否为周期函数?周期函数的定义域有什么特点?
周期函数的定义域一定是无限集,而且定义域一定是无上界或无下界。
2.求函数的周期
例1.求下列函数的周期:
---定义法
练习:P36 1.2
二 公式法
例3 求函数 的周期
形如 的最小正周期
——利用图像
例4 周期函数的应用
课堂小结
1 三角函数的周期是三角函数的重要性质之一,周期的求法有定义法,公式法,图像法。
2 周期性体现了它们的函数值随自变量变化而呈周期性变化的规律,因此研究周期函数的问题只需要研究其一个周期
今日作业
书本P46.A组3.10 B组3
( 2 ,0)
( ,-1)
( ,0)
( ,1)
要点回顾.
正弦曲线、余弦函数的图象
1)图象作法---
几何法
五点法
2)正弦曲线、余弦曲线
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
余弦曲线
(0,1)
( ,0)
( ,-1)
( ,0)
( 2 ,1)
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦曲线
(0,0)
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
x
y
1
-1
探索发现
观察正弦函数图像的特点
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
探索发现
观察余弦函数图像,是否也具有上述特点?
像这样一种函数叫做周期函数.
周期函数的定义:对于函数 f(x), 如果
存在一个非零常数T,使得当 x 取定义域
内的每一个值时,都有 f (x+T)= f(x),那么
函数 f(x) 就叫做周期函数,非零常数T叫
做这个函数的周期 .
注意:
1°周期函数x∈定义域M,则必
有 x +T∈M.
2°对“每一个值”的理解:只要有一个
反例, 则 f (x)就不为周期函数.
3°T往往是多值的(如 y = sinx 2π, 4π,
…, -2π, -4π, …都是周期)周期T中最
小正数叫做 f (x)的最小正周期 (有些周
期函数没有最小正周期) .
本书中涉及的周期,如果不加特别说明,一般都是指函数的最小正周期
周期概念的拓展
1 函数f(x)=sinx(x≥0)是否为周期函数?函数f(x)=sinx(x≤0)是否为周期函数?
2 函数f(x)=sinx(x>0)是否为周期函数?函数f(x)=sinx(x≠3kπ)是否为周期函数?
3 函数f(x)=sinx,x∈[0,10π]是否为周期函数?周期函数的定义域有什么特点?
周期函数的定义域一定是无限集,而且定义域一定是无上界或无下界。
2.求函数的周期
例1.求下列函数的周期:
---定义法
练习:P36 1.2
二 公式法
例3 求函数 的周期
形如 的最小正周期
——利用图像
例4 周期函数的应用
课堂小结
1 三角函数的周期是三角函数的重要性质之一,周期的求法有定义法,公式法,图像法。
2 周期性体现了它们的函数值随自变量变化而呈周期性变化的规律,因此研究周期函数的问题只需要研究其一个周期
今日作业
书本P46.A组3.10 B组3
