1.4.2正弦函数、余弦函数的性质(三)》
文档属性
| 名称 | 1.4.2正弦函数、余弦函数的性质(三)》 |

|
|
| 格式 | rar | ||
| 文件大小 | 208.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-20 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
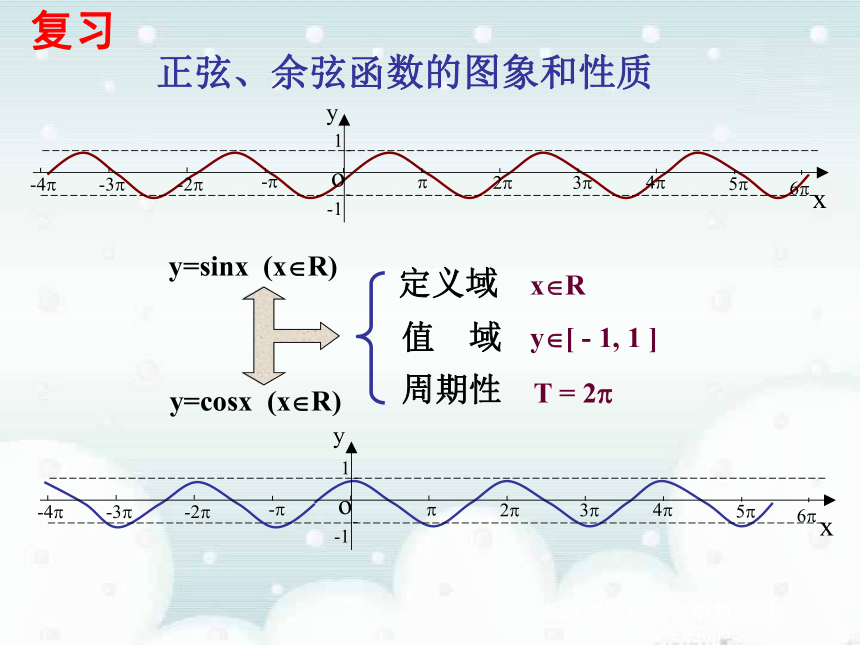
正弦、余弦函数的图象和性质
y=sinx (x R)
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
y
y=cosx (x R)
定义域
值 域
周期性
x R
y [ - 1, 1 ]
T = 2
复习
2 函数的奇偶性
一般地,
如果对于函数f( x )的定义域内任意一个x,都有f(- x )= f( x ),那么就说f( x )是偶函数
如果对于函数f( x )的定义域内任意一个x,都有f(- x )= -f( x ),那么就说f( x )是奇函数
奇函数图像关于原点对称,偶函数图像关于y轴对称
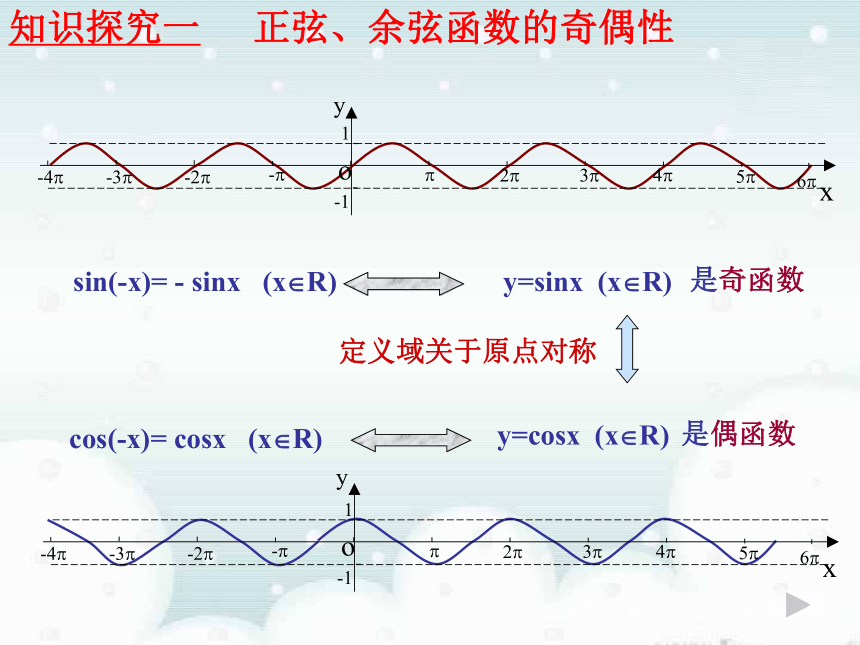
sin(-x)= - sinx (x R)
y=sinx (x R)
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
是奇函数
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
y
cos(-x)= cosx (x R)
y=cosx (x R)
是偶函数
定义域关于原点对称
正弦、余弦函数的奇偶性
知识探究一
例1.判断下列函数的奇偶性:
注意:先求函数的定义域是判断奇偶性的大前提
知识探究二: 正,余弦曲线的对称性
思考1:正弦曲线除了关于原点对称外,是否还关于其它的点对称?
正弦曲线是中心对称图形,其所有的
对称中心坐标是 ;
思考2:正弦曲线是否还具有其它对称性?
正弦曲线是轴对称图形,其所有
的对称轴方程是
思考3:余弦曲线除了关于y轴对称外,是否还关于其它的点和直线对称?
余弦曲线是中心对称图形,其所有的对称中心坐标是 ;
余弦曲线是轴对称图形,其所有的对称轴方程是
正弦曲线,余弦曲线的对称轴一定分别过正弦曲线,余弦曲线的最高点或最低点,即此时的正弦值余弦值取最大值或最小值。
正弦曲线,余弦曲线的对称中心一定分别过正弦曲线,余弦曲线与x轴的交点,即此时的正弦值或余弦值为0
[答案] A
课堂小结
奇偶性是正弦函数,余弦函数的重要性质之一,它揭示了正余弦函数的一条整体性质反应在图像上就是对称性
判断函数奇偶性应先判断定义域是否关于原点对称
作业:判断下列函数的奇偶性
正弦、余弦函数的图象和性质
y=sinx (x R)
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
y
y=cosx (x R)
定义域
值 域
周期性
x R
y [ - 1, 1 ]
T = 2
复习
2 函数的奇偶性
一般地,
如果对于函数f( x )的定义域内任意一个x,都有f(- x )= f( x ),那么就说f( x )是偶函数
如果对于函数f( x )的定义域内任意一个x,都有f(- x )= -f( x ),那么就说f( x )是奇函数
奇函数图像关于原点对称,偶函数图像关于y轴对称
sin(-x)= - sinx (x R)
y=sinx (x R)
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
是奇函数
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
y
cos(-x)= cosx (x R)
y=cosx (x R)
是偶函数
定义域关于原点对称
正弦、余弦函数的奇偶性
知识探究一
例1.判断下列函数的奇偶性:
注意:先求函数的定义域是判断奇偶性的大前提
知识探究二: 正,余弦曲线的对称性
思考1:正弦曲线除了关于原点对称外,是否还关于其它的点对称?
正弦曲线是中心对称图形,其所有的
对称中心坐标是 ;
思考2:正弦曲线是否还具有其它对称性?
正弦曲线是轴对称图形,其所有
的对称轴方程是
思考3:余弦曲线除了关于y轴对称外,是否还关于其它的点和直线对称?
余弦曲线是中心对称图形,其所有的对称中心坐标是 ;
余弦曲线是轴对称图形,其所有的对称轴方程是
正弦曲线,余弦曲线的对称轴一定分别过正弦曲线,余弦曲线的最高点或最低点,即此时的正弦值余弦值取最大值或最小值。
正弦曲线,余弦曲线的对称中心一定分别过正弦曲线,余弦曲线与x轴的交点,即此时的正弦值或余弦值为0
[答案] A
课堂小结
奇偶性是正弦函数,余弦函数的重要性质之一,它揭示了正余弦函数的一条整体性质反应在图像上就是对称性
判断函数奇偶性应先判断定义域是否关于原点对称
作业:判断下列函数的奇偶性
