1.4.2正弦函数、余弦函数的性质(四)
文档属性
| 名称 | 1.4.2正弦函数、余弦函数的性质(四) |  | |
| 格式 | rar | ||
| 文件大小 | 110.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-20 13:02:09 | ||
图片预览




文档简介
(共13张PPT)
正弦、余弦函数的图象和性质
y=sinx (x R)
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
y
y=cosx (x R)
定义域
值 域
周期性
x R
y [ - 1, 1 ]
T = 2
奇偶性
y=sinx (x R)是奇函数
y=cosx (x R)是偶函数
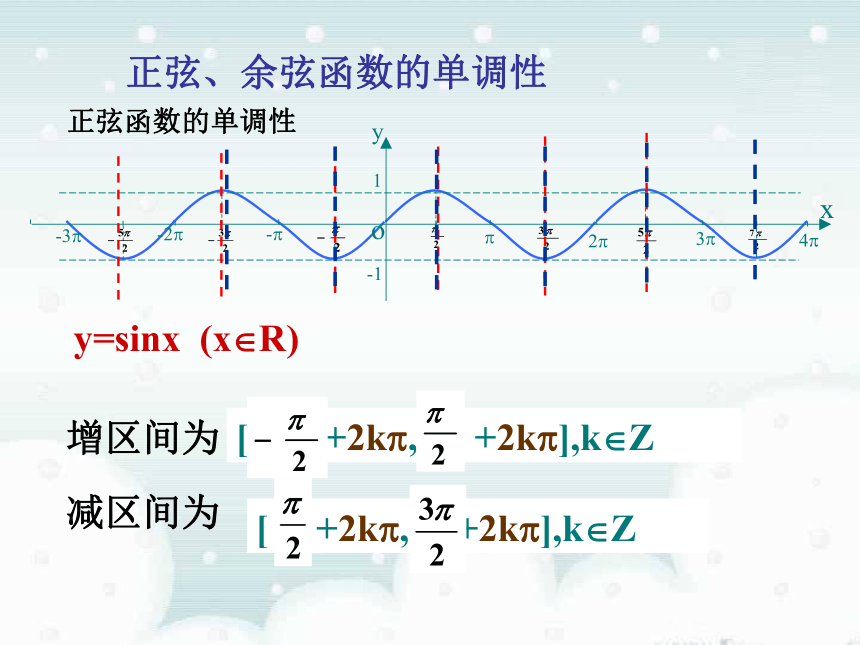
正弦、余弦函数的单调性
正弦函数的单调性
y=sinx (x R)
增区间为
x
y
o
-
-1
2
3
4
-2
-3
1
减区间为
[ +2k , +2k ],k Z
[ +2k , +2k ],k Z
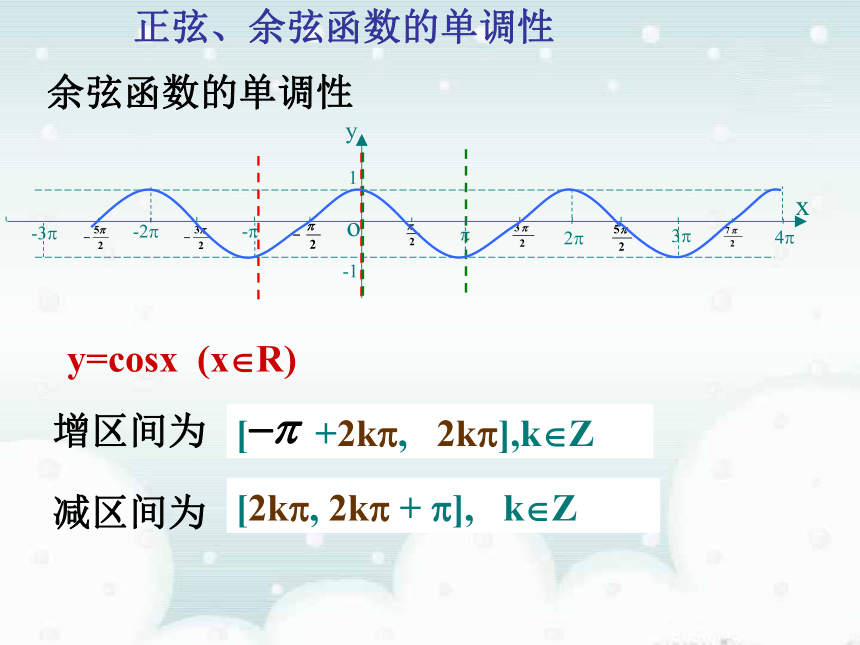
正弦、余弦函数的单调性
余弦函数的单调性
y=cosx (x R)
增区间为
[ +2k , 2k ],k Z
减区间为
[2k , 2k + ], k Z
y
x
o
-
-1
2
3
4
-2
-3
1
例1 比较下列各组数的大小:
分析:化为同一单调区间的上的同名函数,
再利用三角函数单调性作出判断。
解:
(1)
且正弦函数 在区间
上是增函数,所以
解:
(2)
且函数 是减函数
即
练习:P41 5
还有其他方法来比较吗?
作单位圆用三角函数线
变式:你能求函数
的单调区间吗?
1 求形如 或
的函数的单调区间,首先把x的系数化为正的,再
利用整体代换,把 代入相应不等式中,求
解相应的x的范围
求复合函数的单调区间时,要先求定义域,同时
还要注意内层,外层函数的单调性。
小 结:
正弦、余弦函数的奇偶性、单调性
奇偶性
单调性(单调区间)
奇函数
偶函数
[ +2k , +2k ],k Z
单调递增
[ +2k , +2k ],k Z
单调递减
[ +2k , 2k ],k Z
单调递增
[2k , 2k + ], k Z
单调递减
函数
余弦函数
正弦函数
求函数的单调区间:
1. 直接利用相关性质
2. 复合函数的单调性
3. 利用图象寻找单调区间
函 数
性 质 y= sinx (k∈z) y= cosx (k∈z)
定义域
值域
最值及相应的 x的集合
周期性
奇偶性
单调性
对称中心
对称轴
x∈ R
x∈ R
[-1,1]
[-1,1]
x= 2kπ时 ymax=1
x= 2kπ+ π时 ymin=-1
周期为T=2π
周期为T=2π
奇函数
偶函数
在x∈[2kπ, 2kπ+ π ]
上都是增函数 ,
在x∈[2kπ- π , 2kπ ]
上都是减函数 。
(kπ,0)
x = kπ
x= 2kπ+ 时 ymax=1
x=2kπ- 时 ymin=-1
π
2
π
2
在x∈[2kπ- , 2kπ+ ] 上都是增函数 , 在x∈[2kπ+ ,2kπ+ ]上都是减函数.
π
2
π
2
π
2
3π
2
(kπ+ ,0)
π
2
x = kπ+
π
2
正弦、余弦函数的图象和性质
y=sinx (x R)
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
x
6
o
-
-1
2
3
4
5
-2
-3
-4
1
y
y=cosx (x R)
定义域
值 域
周期性
x R
y [ - 1, 1 ]
T = 2
奇偶性
y=sinx (x R)是奇函数
y=cosx (x R)是偶函数
正弦、余弦函数的单调性
正弦函数的单调性
y=sinx (x R)
增区间为
x
y
o
-
-1
2
3
4
-2
-3
1
减区间为
[ +2k , +2k ],k Z
[ +2k , +2k ],k Z
正弦、余弦函数的单调性
余弦函数的单调性
y=cosx (x R)
增区间为
[ +2k , 2k ],k Z
减区间为
[2k , 2k + ], k Z
y
x
o
-
-1
2
3
4
-2
-3
1
例1 比较下列各组数的大小:
分析:化为同一单调区间的上的同名函数,
再利用三角函数单调性作出判断。
解:
(1)
且正弦函数 在区间
上是增函数,所以
解:
(2)
且函数 是减函数
即
练习:P41 5
还有其他方法来比较吗?
作单位圆用三角函数线
变式:你能求函数
的单调区间吗?
1 求形如 或
的函数的单调区间,首先把x的系数化为正的,再
利用整体代换,把 代入相应不等式中,求
解相应的x的范围
求复合函数的单调区间时,要先求定义域,同时
还要注意内层,外层函数的单调性。
小 结:
正弦、余弦函数的奇偶性、单调性
奇偶性
单调性(单调区间)
奇函数
偶函数
[ +2k , +2k ],k Z
单调递增
[ +2k , +2k ],k Z
单调递减
[ +2k , 2k ],k Z
单调递增
[2k , 2k + ], k Z
单调递减
函数
余弦函数
正弦函数
求函数的单调区间:
1. 直接利用相关性质
2. 复合函数的单调性
3. 利用图象寻找单调区间
函 数
性 质 y= sinx (k∈z) y= cosx (k∈z)
定义域
值域
最值及相应的 x的集合
周期性
奇偶性
单调性
对称中心
对称轴
x∈ R
x∈ R
[-1,1]
[-1,1]
x= 2kπ时 ymax=1
x= 2kπ+ π时 ymin=-1
周期为T=2π
周期为T=2π
奇函数
偶函数
在x∈[2kπ, 2kπ+ π ]
上都是增函数 ,
在x∈[2kπ- π , 2kπ ]
上都是减函数 。
(kπ,0)
x = kπ
x= 2kπ+ 时 ymax=1
x=2kπ- 时 ymin=-1
π
2
π
2
在x∈[2kπ- , 2kπ+ ] 上都是增函数 , 在x∈[2kπ+ ,2kπ+ ]上都是减函数.
π
2
π
2
π
2
3π
2
(kπ+ ,0)
π
2
x = kπ+
π
2
