1.3-2三角函数的诱导公式)
文档属性
| 名称 | 1.3-2三角函数的诱导公式) |  | |
| 格式 | rar | ||
| 文件大小 | 104.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-20 13:08:03 | ||
图片预览








文档简介
(共21张PPT)
第二课时
问题提出
1.诱导公式一、二、三、四分别反映了2kπ+α(k∈Z)、π+α、-α、 π-α与α的三角函数之间的关系,这四组公式的共同特点是什么?
函数同名,象限定号.
2.对形如π-α、π+α的角的三角函数可以转化为α角的三角函数,对形如 、 的角的三角函数与α角
的三角函数,是否也存在着某种关系,需要我们作进一步的探究.
知识探究(一): 的诱导公式
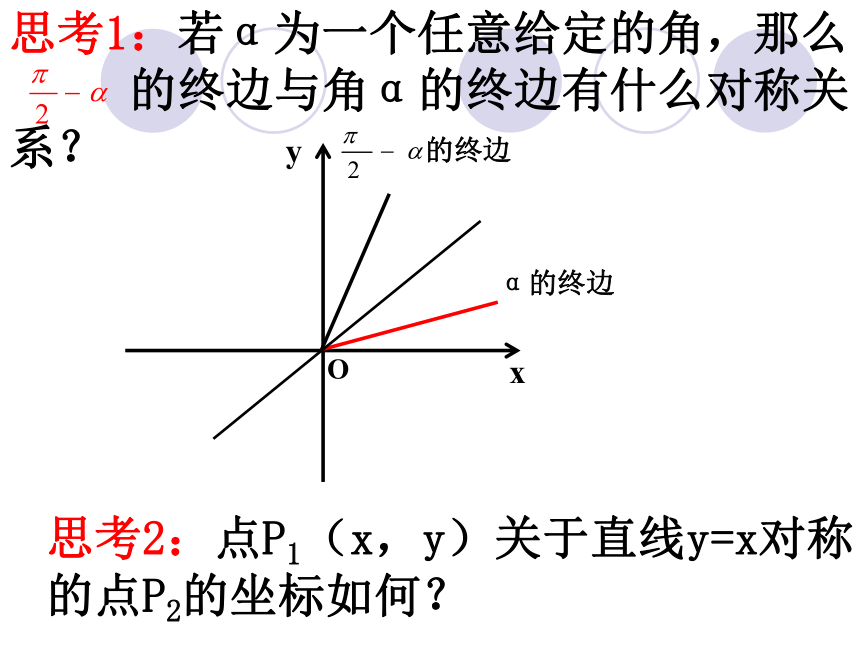
思考1:若α为一个任意给定的角,那么 的终边与角α的终边有什么对称关系?
思考2:点P1(x,y)关于直线y=x对称的点P2的坐标如何?
思考3:设角α的终边与单位圆的交点为P1(x,y),则 的终边与单位圆的交点为P2,根据三角函数的定义,你能获得哪些结论?
思考2:点P1(x,y)关于直线y=x对称的点P2的坐标如何?
思考1:若α为一个任意给定的角,那么
的终边与角α的终边有什么对称关系?
α的终边
O
x
y
的终边
思考3:设角α的终边与单位圆的交点为P1(x,y),则 的终边与单位圆的交点为P2(y,x),根据三角函数的定义,你能获得哪些结论?
α的终边
P1(x,y)
O
x
y
的终边
P2(y,x)
公式五:
知识探究(二): 的诱导公式
思考1: 与 有什么内在联系?
思考2:根据相关诱导公式推导,
, 分别等于什么?
思考3:根据相关诱导公式推导,
分别等于什么?
思考3:根据相关诱导公式推导,
, 分别等于什么?
公式六:
思考2: 与 有什么内在联系?
思考3:根据相关诱导公式推导,
分别等于什么?
诱导公式的变形
诱导公式的变形
共同点:
函数名改变,符号看象限
公式回顾和总结
公式回顾和总结
共同点:
函数名不变,符号看象限
角的形式看为
利用诱导公式就可以将任意角的三角函数转化为锐角的三角函数。其化简方向仍为:“负化正,大化小,化到锐角为终了”。
意义:
口诀:奇变偶不变,符号看象限
例题分析
例1 化简:
求值:
挖掘角的相互关系,寻求诱导公式的应用
互余关系
挖掘角的相互关系,寻求诱导公式的应用
互补关系
牛刀小试
练习:已知 ,求
的值.
2.诱导公式是三角变换的基本公式,其中角α可以是一个单角,也可以是一个复角,应用时要注意整体把握、灵活变通.
小结作业
1.诱导公式反映了各种不同形式的角的三角函数之间的相互关系,并具有一定的规律性,“奇变偶不变,符号看象限”,是记住这些公式的有效方法.
3 利用诱导公式可以求所有角的三角函数值
作业: P29习题1.3 A组:3.
B组:1,2.
第二课时
问题提出
1.诱导公式一、二、三、四分别反映了2kπ+α(k∈Z)、π+α、-α、 π-α与α的三角函数之间的关系,这四组公式的共同特点是什么?
函数同名,象限定号.
2.对形如π-α、π+α的角的三角函数可以转化为α角的三角函数,对形如 、 的角的三角函数与α角
的三角函数,是否也存在着某种关系,需要我们作进一步的探究.
知识探究(一): 的诱导公式
思考1:若α为一个任意给定的角,那么 的终边与角α的终边有什么对称关系?
思考2:点P1(x,y)关于直线y=x对称的点P2的坐标如何?
思考3:设角α的终边与单位圆的交点为P1(x,y),则 的终边与单位圆的交点为P2,根据三角函数的定义,你能获得哪些结论?
思考2:点P1(x,y)关于直线y=x对称的点P2的坐标如何?
思考1:若α为一个任意给定的角,那么
的终边与角α的终边有什么对称关系?
α的终边
O
x
y
的终边
思考3:设角α的终边与单位圆的交点为P1(x,y),则 的终边与单位圆的交点为P2(y,x),根据三角函数的定义,你能获得哪些结论?
α的终边
P1(x,y)
O
x
y
的终边
P2(y,x)
公式五:
知识探究(二): 的诱导公式
思考1: 与 有什么内在联系?
思考2:根据相关诱导公式推导,
, 分别等于什么?
思考3:根据相关诱导公式推导,
分别等于什么?
思考3:根据相关诱导公式推导,
, 分别等于什么?
公式六:
思考2: 与 有什么内在联系?
思考3:根据相关诱导公式推导,
分别等于什么?
诱导公式的变形
诱导公式的变形
共同点:
函数名改变,符号看象限
公式回顾和总结
公式回顾和总结
共同点:
函数名不变,符号看象限
角的形式看为
利用诱导公式就可以将任意角的三角函数转化为锐角的三角函数。其化简方向仍为:“负化正,大化小,化到锐角为终了”。
意义:
口诀:奇变偶不变,符号看象限
例题分析
例1 化简:
求值:
挖掘角的相互关系,寻求诱导公式的应用
互余关系
挖掘角的相互关系,寻求诱导公式的应用
互补关系
牛刀小试
练习:已知 ,求
的值.
2.诱导公式是三角变换的基本公式,其中角α可以是一个单角,也可以是一个复角,应用时要注意整体把握、灵活变通.
小结作业
1.诱导公式反映了各种不同形式的角的三角函数之间的相互关系,并具有一定的规律性,“奇变偶不变,符号看象限”,是记住这些公式的有效方法.
3 利用诱导公式可以求所有角的三角函数值
作业: P29习题1.3 A组:3.
B组:1,2.
