数学:1.5《函数y=asin(ωx+φ)的图象》课件(新人教a版必修4)
文档属性
| 名称 | 数学:1.5《函数y=asin(ωx+φ)的图象》课件(新人教a版必修4) |  | |
| 格式 | rar | ||
| 文件大小 | 151.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-20 13:09:47 | ||
图片预览







文档简介
(共29张PPT)
1.5函数y=Asin(ωx+φ)的图象
教学目的:
1、理解振幅变换和周期变换和平移变换;会用图象变换的方法画y=Asin(ωx+ )的图象 ;
2、会用“五点法”画y=Asin(ωx+ )的图象 ;
3、会求一些函数的振幅、周期、最值等 ;
4、渗透分类讨论的数学思想,提高分析和解决问题的能力 。
教学重点、难点:
难点:理解振幅变换和周期变换和平移变换 。
重点:用图象变换的方法画y=Asin(ωx+ )的图象 。
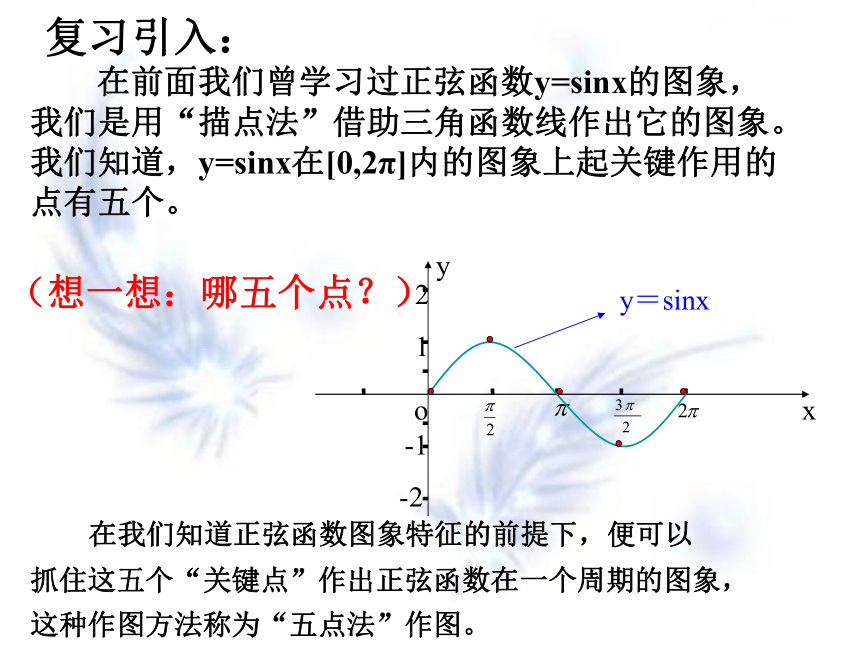
在前面我们曾学习过正弦函数y=sinx的图象,我们是用“描点法”借助三角函数线作出它的图象。我们知道,y=sinx在[0,2π]内的图象上起关键作用的点有五个。
复习引入:
y
o
x
1
2
-1
-2
y=sinx
(想一想:哪五个点?)
在我们知道正弦函数图象特征的前提下,便可以
抓住这五个“关键点”作出正弦函数在一个周期的图象,
这种作图方法称为“五点法”作图。
例1:作函数y = 2sin( x- )的简图。
解:
列表
0
0
0
y
0
-2
0
2
0
Sin(Z)
-1
1
x
2π
π
0
Z
2π
5π
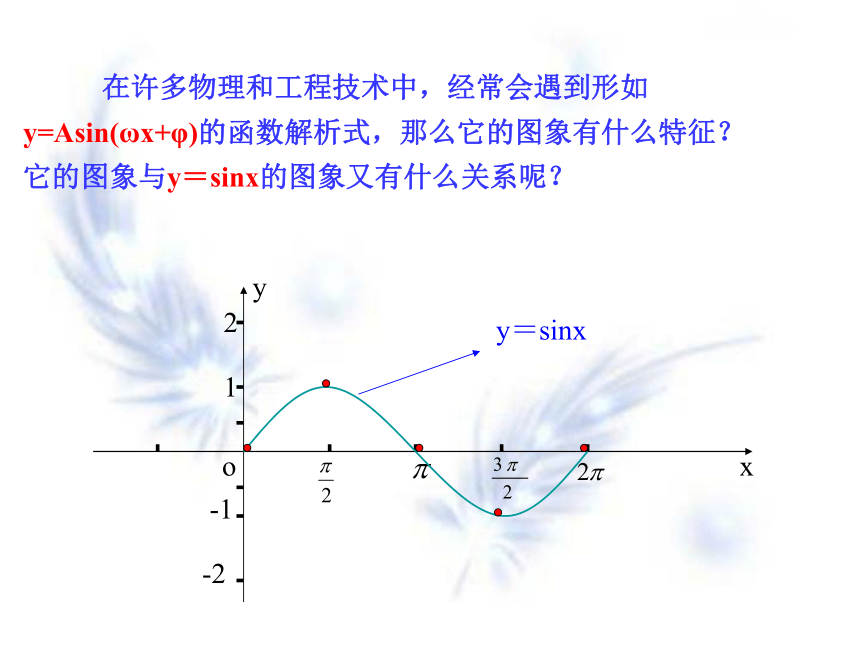
在许多物理和工程技术中,经常会遇到形如
y=Asin(ωx+φ)的函数解析式,那么它的图象有什么特征?
它的图象与y=sinx的图象又有什么关系呢?
y
o
x
1
2
-1
-2
y=sinx
y
o
x
1
2
-1
-2
例1.作出y=2sinx和y= sinx在[0,2π]内的简图,并与y=sinx在[0,2π]内的图象进行比较
y=2sinx
y=sinx
2
1
y= sinx
π
6
想一想
如何由y=sinx的图象变换得到
1
2
0
2
0
2
0
sin
2
-
x
y
o
x
1
2
-1
-2
例1.作出y=2sinx, y= sinx在[0,2π]内的简图,并与y=sinx的在[0,2π]内图象进行比较
y=2sinx
y=sinx
2
1
y= sinx
1
2
y=2sinx
刚才的变换可简记为:
y=sinx的图象
y=2sinx的图象
各点的纵坐标伸长到原来的2倍
(横坐标不变)
y=sinx的图象
2
1
y= sinx的图象
各点的纵坐标缩短到原来的1/2倍
(横坐标不变)
例1.作y=2sinx, y= sinx在[0,2π]内的简图,并与y=sinx在[0,2π]内的图象进行比较
1
2
刚才的变换可简记为:
y=sinx的图象
y=2sinx的图象
各点的纵坐标伸长到原来的2倍
y=sinx的图象
2
1
y= sinx的图象
(横坐标不变)
各点的纵坐标缩短到原来的1/2倍
(横坐标不变)
y=Asinx (其中A>0) 的图象可看成是由y=sinx的图象上的所有点的纵坐标伸长(A>1时) 或 缩短(0注:A引起图象的纵向伸缩,它决定函数的最大(最小)
值,我们把A 叫做振幅。
结论:
练习巩固
A引起图象的纵向伸缩,那么当ω发生变化时,会引起什么变换呢?
1.函数y= sinx,y=4sinx的振幅分别是多少?
它们的图象是由y=sinx的图象作怎样的变换而得到?
3
1
解:
把函数y=sinx的图象上所有点的纵坐标缩短到原来的1/3倍(横坐标不变)即得到y= sinx的图象.
3
1
它们的振幅分别是1/3,4
把函数y=sinx的图象上所有点的纵坐标伸长到原来的4倍(横坐标不变)即得到y=4sinx的图象.
启发过渡:
例1.作y=2sinx, y= sinx在[0,2π]内的简图,并与y=sinx在[0,2π]内的图象进行比较
1
2
y=Asinx (其中A>0) 的图象可看成是由y=sinx的图象上的所有点的纵坐标伸长(A>1时) 或 缩短(0结论:
例2.画出y=sin2x ,y=sin x在[0,2π]内的简图,并与y=sinx在[0,2π]内的图象比较。
解:先作函数y=sin2x在[0,2π]内的图象。
其周期T=______________
ω
=π
0
1
0
1
0
2
sin
-
x
y
o
x
1
-1
3π
-π
想一想
Y=sin x
2
1
Y=sin2x
Y=sinx
例2.画出y=sin2x ,y=sin x在[0,2π]内的简图,并与y=sinx在[0,2π]内的图象比较。
y
o
x
1
-1
3π
-π
Y=sin x
2
1
Y=sin2x
Y=sinx
刚才的变换可简记为:
Y=sinx的图象 y=sin2x的图象
各点的横坐标缩短到原来的1/2倍
Y=sinx的图象 y=sin x的图象
各点的横坐标伸长到原来的2倍
1
2
(纵坐标不变)
(纵坐标不变)
例2.画出y=sin2x ,y=sin x在[0,2π]内的简图,并与y=sinx在[0,2π]内的图象比较。
刚才的变换可简记为:
Y=sinx的图象 y=sin2x的图象
各点的横坐标缩短到原来的1/2倍
Y=sinx的图象 y=sin x的图象
各点的横坐标伸长到原来的2倍
1
2
(纵坐标不变)
(纵坐标不变)
结论:函数y=sinωx (其中ω>0) 的图象,可看
作把y=sinx图象上所有点的横坐标伸长
(当 0<ω<1)或缩短(当ω>1)到原来的1/ω
倍(纵坐标不变)而得到.
注: ω决定函数的周期T=2π/ω,它引起横
向伸缩(可简记为:小伸大缩).
2.函数y=sin3x的周期是多少 它的图象是由y=sinx 的图
象作什么变换而得到
巩固练习:
Y=sinx y=sin3x的图象
各点的横坐标缩短到原来的1/3倍
(纵坐标不变)
解:
T=2π/ω=2π/3
3.把正弦曲线y=sinx图象上所有点的横坐标伸长到原来的
5倍(纵坐标不变),就得到函数______________的图象.
1
5
_
Y=sin x
例2.画出y=sin2x ,y=sin x的简图,并与y=sinx的图象比较。
结论:函数y=sinωx (其中ω>0) 的图象,可看 作把y=sinx图象上所有点的横坐标伸长 (当 0<ω<1)或缩短(当ω>1)到原来的1/ω倍(纵坐标不变)而得到.
为了得到y=3sin(2x+π/5)的图象,只需将函数y=3sin(x+π/5)的图象上各点怎样变化?
探究:
例3.画出 和 的简图(用图象变换法).
Y=sinx的图象 的图象
向左平移π/3个单位长度
Y=sinx的图象 的图象
向右平移π/4个单位长度
o
x
1
-1
y
4
p
3
p
Y=sin(x+ )
π
3
Y=sin(x- )
π
4
Y=sin(x+ )
π
3
Y=sin(x- )
π
4
Y=sinx
Y=sin(x+ )
π
3
π
Y=sin(x- )
4
注:φ引起图象的左右平移,它改变图象的位置,不改变图象的形状.φ叫做初相.
结论:y=sin(x+φ)的图象,可以看作把y=sinx的图象向左(当φ>0)或向右(当φ<0)平移|φ|个单位长度而得到.(简记为:左加右减)
注:φ引起图象的左右平移,它改变图象的位置,不改变图象的形状.φ叫做初相.
结论:y=sin(x+φ)的图象,可以看作把y=sinx的图象向左(当φ>0)或向右(当φ<0)平移|φ|个单位长度而得到.(简记为:左加右减)
巩固练习:
5.函数 的初相是_____,它的图象是由
y=sinx的图象____平移_____个单位长度而得到.
12
π
4.把函数y=sinx 的图象向右平移 个单位长度,得到
函数 ______________的图象.
Y=sin(x- )
12
π
5
p
Y=sin(x+ )
5
p
5
p
左
例3.画出 和 的简图(用图象变换法).
Y=sin(x+ )
π
3
Y=sin(x- )
π
4
问题:把y=sin2x的图象经过怎样的变换就得到
y=sin(2x+ )的图象
3
p
想一想
-3
o
x
1
2
-1
-2
3
y
向左平移π/3个单位长度
横坐标缩短到原来的1/2倍
(纵坐标不变)
纵坐标伸长到原来的3倍
(横坐标不变)
y=sinx的图象
y=sin(x+π/3)的图象
第1步:
第2步:
y=sin(x+π/3)的图象
y=sin(2x+ π/3)的图象
y=sin(2x+ π/3)的图象
y=3sin(2x+ π/3)的图象
第3步:
y=sinx
y=sin(x+π/3)
y=sin(2x+ π/3)
y=3sin(2x+ π/3)
y=3sin(2x+ π/3)
思考:还可以如何变化?
将函数
的图象变换为函数
的图象。
将函数
的图象变换为函数
的图象。
解法2:
y=3sin(2x+ π/3)的图象
:
纵坐标伸长到原来的3倍
(横坐标不变)
y=Asin( x+ ) (A>0, >0) 的图象可由y=sinx经过如下变换得到:
y=sinx
向左( >0)或向右( <0)
平移 个单位
y=sin(x+ )
横坐标变为原来的 倍
纵坐标不变
1
y=sin( x+ )
纵坐标变为原来的A倍
横坐标不变
y=Asin( x+ )
或:
y=sinx
y=sin x
横坐标变为原来的 倍
纵坐标不变
1
纵坐标变为原来的A倍
横坐标不变
y=Asin( x+ )
向左( >0)或向右( <0)
平移 个单位
y=sin (x+ )
=sin( x+ )
①先平移变换再周期变换
②先周期变换再平移变换
例2 如图是函数
的图象,确定A、
、
的值。
解:显然A=2
解法1:由图知当
时,y=0 故有
所求函数解析式为
解法2:由图象可知将
的图象向左移
即得
,即
所求函数解析式为
小结:
1.对于函数 y=Asin( x+ ) (A>0, >0):
A --- 振幅,
--- 周期,
--- 频率,
x+ --- 相位,
--- 初相.
2.图象的变换:
(1)伸缩变换
振幅变换
周期变换
(2)平移变换
上下平移
左右平移
( ----- 形状变换)
( ----- 位置变换)
y=sinx
向左( >0)或向右( <0)
平移 个单位
y=sin(x+ )
横坐标变为原来的 倍
纵坐标不变
1
y=sin( x+ )
纵坐标变为原来的A倍
横坐标不变
y=Asin( x+ )
y=Asin( x+ ) (A>0, >0) 的图象可由y=sinx经过如下变换得到:
四、课堂练习
P62练习题1、2、3、4、7
1.由解析式作图:
由函数y=Asin( x+ )+B的解析式作图:
(1)五点作图法; (2)利用函数图象的变换.
2.看图识解析式:
抓住图象的特征,如关键点,周期,振幅,对称轴等.
小结
P65习题 A组第1、3题
B组 第2、3题
六、课后作业:
一、平移变换
二、对称变换
三、伸缩变换
三、伸缩变换
1.5函数y=Asin(ωx+φ)的图象
教学目的:
1、理解振幅变换和周期变换和平移变换;会用图象变换的方法画y=Asin(ωx+ )的图象 ;
2、会用“五点法”画y=Asin(ωx+ )的图象 ;
3、会求一些函数的振幅、周期、最值等 ;
4、渗透分类讨论的数学思想,提高分析和解决问题的能力 。
教学重点、难点:
难点:理解振幅变换和周期变换和平移变换 。
重点:用图象变换的方法画y=Asin(ωx+ )的图象 。
在前面我们曾学习过正弦函数y=sinx的图象,我们是用“描点法”借助三角函数线作出它的图象。我们知道,y=sinx在[0,2π]内的图象上起关键作用的点有五个。
复习引入:
y
o
x
1
2
-1
-2
y=sinx
(想一想:哪五个点?)
在我们知道正弦函数图象特征的前提下,便可以
抓住这五个“关键点”作出正弦函数在一个周期的图象,
这种作图方法称为“五点法”作图。
例1:作函数y = 2sin( x- )的简图。
解:
列表
0
0
0
y
0
-2
0
2
0
Sin(Z)
-1
1
x
2π
π
0
Z
2π
5π
在许多物理和工程技术中,经常会遇到形如
y=Asin(ωx+φ)的函数解析式,那么它的图象有什么特征?
它的图象与y=sinx的图象又有什么关系呢?
y
o
x
1
2
-1
-2
y=sinx
y
o
x
1
2
-1
-2
例1.作出y=2sinx和y= sinx在[0,2π]内的简图,并与y=sinx在[0,2π]内的图象进行比较
y=2sinx
y=sinx
2
1
y= sinx
π
6
想一想
如何由y=sinx的图象变换得到
1
2
0
2
0
2
0
sin
2
-
x
y
o
x
1
2
-1
-2
例1.作出y=2sinx, y= sinx在[0,2π]内的简图,并与y=sinx的在[0,2π]内图象进行比较
y=2sinx
y=sinx
2
1
y= sinx
1
2
y=2sinx
刚才的变换可简记为:
y=sinx的图象
y=2sinx的图象
各点的纵坐标伸长到原来的2倍
(横坐标不变)
y=sinx的图象
2
1
y= sinx的图象
各点的纵坐标缩短到原来的1/2倍
(横坐标不变)
例1.作y=2sinx, y= sinx在[0,2π]内的简图,并与y=sinx在[0,2π]内的图象进行比较
1
2
刚才的变换可简记为:
y=sinx的图象
y=2sinx的图象
各点的纵坐标伸长到原来的2倍
y=sinx的图象
2
1
y= sinx的图象
(横坐标不变)
各点的纵坐标缩短到原来的1/2倍
(横坐标不变)
y=Asinx (其中A>0) 的图象可看成是由y=sinx的图象上的所有点的纵坐标伸长(A>1时) 或 缩短(0
值,我们把A 叫做振幅。
结论:
练习巩固
A引起图象的纵向伸缩,那么当ω发生变化时,会引起什么变换呢?
1.函数y= sinx,y=4sinx的振幅分别是多少?
它们的图象是由y=sinx的图象作怎样的变换而得到?
3
1
解:
把函数y=sinx的图象上所有点的纵坐标缩短到原来的1/3倍(横坐标不变)即得到y= sinx的图象.
3
1
它们的振幅分别是1/3,4
把函数y=sinx的图象上所有点的纵坐标伸长到原来的4倍(横坐标不变)即得到y=4sinx的图象.
启发过渡:
例1.作y=2sinx, y= sinx在[0,2π]内的简图,并与y=sinx在[0,2π]内的图象进行比较
1
2
y=Asinx (其中A>0) 的图象可看成是由y=sinx的图象上的所有点的纵坐标伸长(A>1时) 或 缩短(0
例2.画出y=sin2x ,y=sin x在[0,2π]内的简图,并与y=sinx在[0,2π]内的图象比较。
解:先作函数y=sin2x在[0,2π]内的图象。
其周期T=______________
ω
=π
0
1
0
1
0
2
sin
-
x
y
o
x
1
-1
3π
-π
想一想
Y=sin x
2
1
Y=sin2x
Y=sinx
例2.画出y=sin2x ,y=sin x在[0,2π]内的简图,并与y=sinx在[0,2π]内的图象比较。
y
o
x
1
-1
3π
-π
Y=sin x
2
1
Y=sin2x
Y=sinx
刚才的变换可简记为:
Y=sinx的图象 y=sin2x的图象
各点的横坐标缩短到原来的1/2倍
Y=sinx的图象 y=sin x的图象
各点的横坐标伸长到原来的2倍
1
2
(纵坐标不变)
(纵坐标不变)
例2.画出y=sin2x ,y=sin x在[0,2π]内的简图,并与y=sinx在[0,2π]内的图象比较。
刚才的变换可简记为:
Y=sinx的图象 y=sin2x的图象
各点的横坐标缩短到原来的1/2倍
Y=sinx的图象 y=sin x的图象
各点的横坐标伸长到原来的2倍
1
2
(纵坐标不变)
(纵坐标不变)
结论:函数y=sinωx (其中ω>0) 的图象,可看
作把y=sinx图象上所有点的横坐标伸长
(当 0<ω<1)或缩短(当ω>1)到原来的1/ω
倍(纵坐标不变)而得到.
注: ω决定函数的周期T=2π/ω,它引起横
向伸缩(可简记为:小伸大缩).
2.函数y=sin3x的周期是多少 它的图象是由y=sinx 的图
象作什么变换而得到
巩固练习:
Y=sinx y=sin3x的图象
各点的横坐标缩短到原来的1/3倍
(纵坐标不变)
解:
T=2π/ω=2π/3
3.把正弦曲线y=sinx图象上所有点的横坐标伸长到原来的
5倍(纵坐标不变),就得到函数______________的图象.
1
5
_
Y=sin x
例2.画出y=sin2x ,y=sin x的简图,并与y=sinx的图象比较。
结论:函数y=sinωx (其中ω>0) 的图象,可看 作把y=sinx图象上所有点的横坐标伸长 (当 0<ω<1)或缩短(当ω>1)到原来的1/ω倍(纵坐标不变)而得到.
为了得到y=3sin(2x+π/5)的图象,只需将函数y=3sin(x+π/5)的图象上各点怎样变化?
探究:
例3.画出 和 的简图(用图象变换法).
Y=sinx的图象 的图象
向左平移π/3个单位长度
Y=sinx的图象 的图象
向右平移π/4个单位长度
o
x
1
-1
y
4
p
3
p
Y=sin(x+ )
π
3
Y=sin(x- )
π
4
Y=sin(x+ )
π
3
Y=sin(x- )
π
4
Y=sinx
Y=sin(x+ )
π
3
π
Y=sin(x- )
4
注:φ引起图象的左右平移,它改变图象的位置,不改变图象的形状.φ叫做初相.
结论:y=sin(x+φ)的图象,可以看作把y=sinx的图象向左(当φ>0)或向右(当φ<0)平移|φ|个单位长度而得到.(简记为:左加右减)
注:φ引起图象的左右平移,它改变图象的位置,不改变图象的形状.φ叫做初相.
结论:y=sin(x+φ)的图象,可以看作把y=sinx的图象向左(当φ>0)或向右(当φ<0)平移|φ|个单位长度而得到.(简记为:左加右减)
巩固练习:
5.函数 的初相是_____,它的图象是由
y=sinx的图象____平移_____个单位长度而得到.
12
π
4.把函数y=sinx 的图象向右平移 个单位长度,得到
函数 ______________的图象.
Y=sin(x- )
12
π
5
p
Y=sin(x+ )
5
p
5
p
左
例3.画出 和 的简图(用图象变换法).
Y=sin(x+ )
π
3
Y=sin(x- )
π
4
问题:把y=sin2x的图象经过怎样的变换就得到
y=sin(2x+ )的图象
3
p
想一想
-3
o
x
1
2
-1
-2
3
y
向左平移π/3个单位长度
横坐标缩短到原来的1/2倍
(纵坐标不变)
纵坐标伸长到原来的3倍
(横坐标不变)
y=sinx的图象
y=sin(x+π/3)的图象
第1步:
第2步:
y=sin(x+π/3)的图象
y=sin(2x+ π/3)的图象
y=sin(2x+ π/3)的图象
y=3sin(2x+ π/3)的图象
第3步:
y=sinx
y=sin(x+π/3)
y=sin(2x+ π/3)
y=3sin(2x+ π/3)
y=3sin(2x+ π/3)
思考:还可以如何变化?
将函数
的图象变换为函数
的图象。
将函数
的图象变换为函数
的图象。
解法2:
y=3sin(2x+ π/3)的图象
:
纵坐标伸长到原来的3倍
(横坐标不变)
y=Asin( x+ ) (A>0, >0) 的图象可由y=sinx经过如下变换得到:
y=sinx
向左( >0)或向右( <0)
平移 个单位
y=sin(x+ )
横坐标变为原来的 倍
纵坐标不变
1
y=sin( x+ )
纵坐标变为原来的A倍
横坐标不变
y=Asin( x+ )
或:
y=sinx
y=sin x
横坐标变为原来的 倍
纵坐标不变
1
纵坐标变为原来的A倍
横坐标不变
y=Asin( x+ )
向左( >0)或向右( <0)
平移 个单位
y=sin (x+ )
=sin( x+ )
①先平移变换再周期变换
②先周期变换再平移变换
例2 如图是函数
的图象,确定A、
、
的值。
解:显然A=2
解法1:由图知当
时,y=0 故有
所求函数解析式为
解法2:由图象可知将
的图象向左移
即得
,即
所求函数解析式为
小结:
1.对于函数 y=Asin( x+ ) (A>0, >0):
A --- 振幅,
--- 周期,
--- 频率,
x+ --- 相位,
--- 初相.
2.图象的变换:
(1)伸缩变换
振幅变换
周期变换
(2)平移变换
上下平移
左右平移
( ----- 形状变换)
( ----- 位置变换)
y=sinx
向左( >0)或向右( <0)
平移 个单位
y=sin(x+ )
横坐标变为原来的 倍
纵坐标不变
1
y=sin( x+ )
纵坐标变为原来的A倍
横坐标不变
y=Asin( x+ )
y=Asin( x+ ) (A>0, >0) 的图象可由y=sinx经过如下变换得到:
四、课堂练习
P62练习题1、2、3、4、7
1.由解析式作图:
由函数y=Asin( x+ )+B的解析式作图:
(1)五点作图法; (2)利用函数图象的变换.
2.看图识解析式:
抓住图象的特征,如关键点,周期,振幅,对称轴等.
小结
P65习题 A组第1、3题
B组 第2、3题
六、课后作业:
一、平移变换
二、对称变换
三、伸缩变换
三、伸缩变换
