人教版八年级下册18.2.3正方形 习题课件(共23张PPT)
文档属性
| 名称 | 人教版八年级下册18.2.3正方形 习题课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 242.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-24 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
有关正方形的习题课
优质课比赛内容
一.正方形的性质
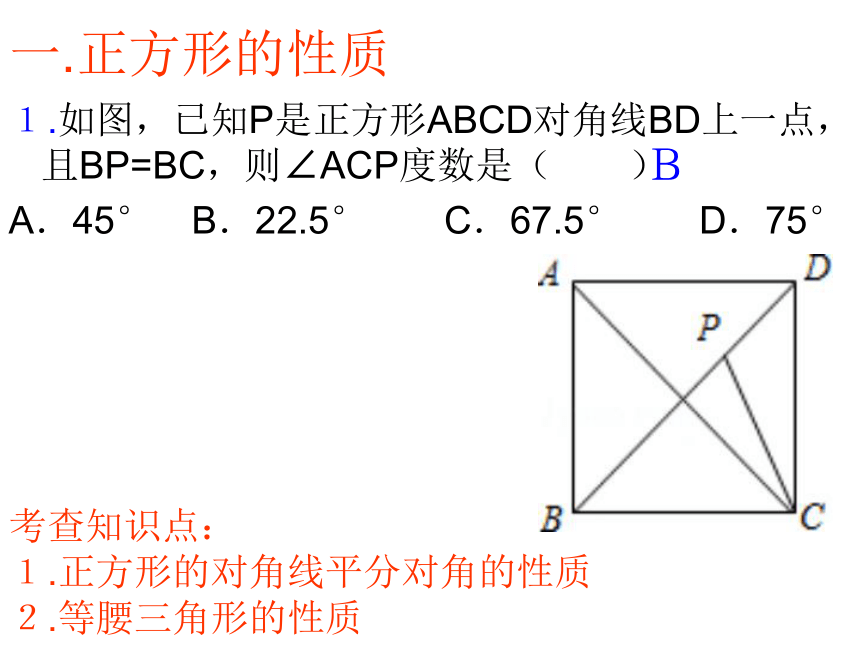
1.如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP度数是( )
A.45° B.22.5° C.67.5° D.75°
考查知识点:
1.正方形的对角线平分对角的性质
2.等腰三角形的性质
B
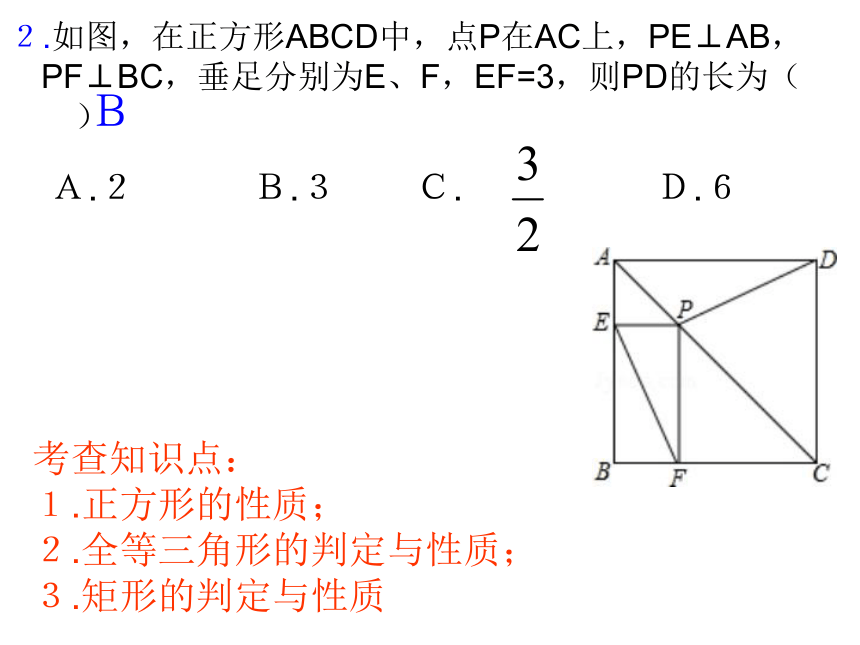
2.如图,在正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E、F,EF=3,则PD的长为( )
A.2 B.3 C. D.6
考查知识点:
1.正方形的性质;
2.全等三角形的判定与性质;
3.矩形的判定与性质
B
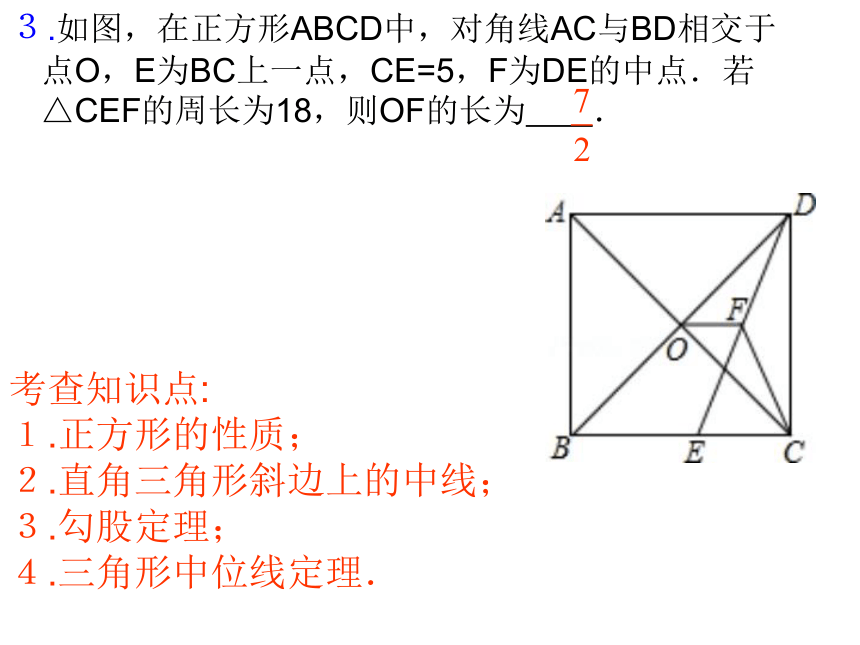
3.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .
考查知识点:
1.正方形的性质;
2.直角三角形斜边上的中线;
3.勾股定理;
4.三角形中位线定理.
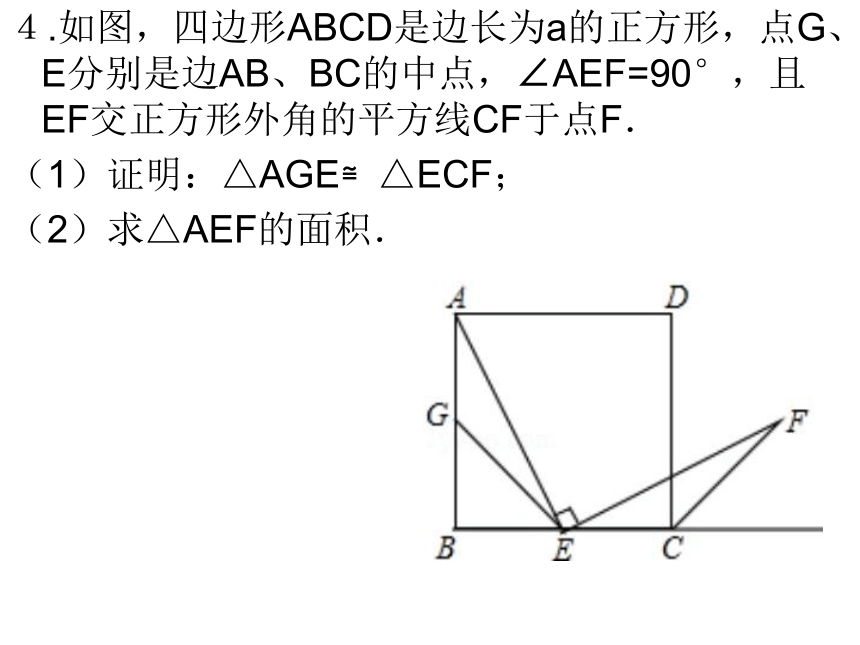
4.如图,四边形ABCD是边长为a的正方形,点G、E分别是边AB、BC的中点,∠AEF=90°,且EF交正方形外角的平方线CF于点F.
(1)证明:△AGE≌△ECF;
(2)求△AEF的面积.
(1)证明:∵G,E分别是正方形ABCD的边 AB,BC的中点
∴AG=GB=BE=EC
且∠AGE=180°﹣45°=135°
又∵CF是∠DCH的平分线
∴∠DCF=∠FCH=45°
∠ECF=90°+45°=135°
∴在△AGE和△ECF中
∴△AGE≌△ECF
(2)解:由△AGE≌△ECF,得AE=EF;
又∵∠AEF=90°,
∴△AEF是等腰直角三角形;
∵AB=a,E为BC中点,
∴BE= BC= AB= a,
根据勾股定理得:AE= =a,
∴S△AEF= a2.
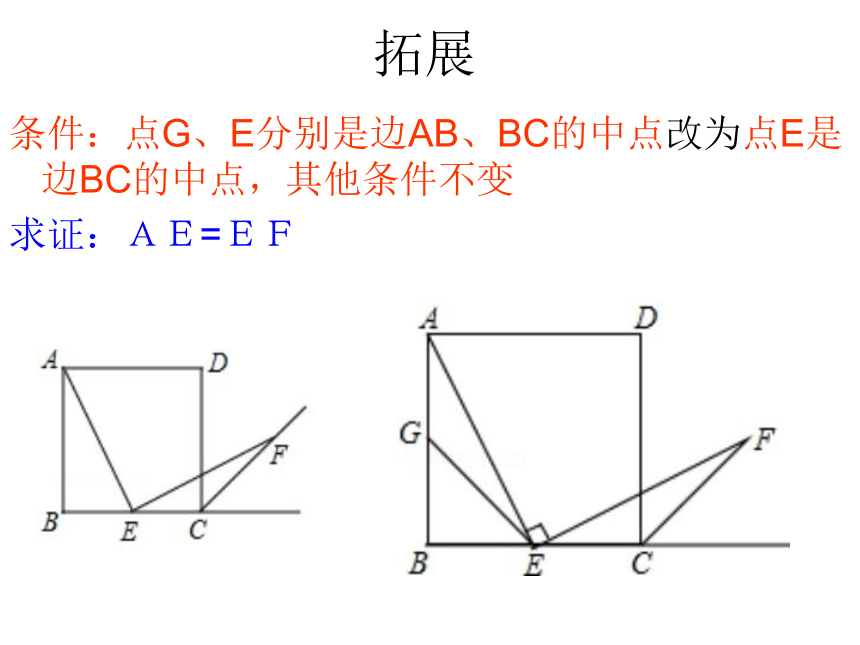
拓展
条件:点G、E分别是边AB、BC的中点改为点E是边BC的中点,其他条件不变
求证:AE=EF
1.下列条件中,不能判定一个平行四边形是正方形的是( )
A.对角线相等且互相垂直
B.一组邻边相等且有一个角是直角
C.对角线相等且一组邻边相等
D.对角线互相平分且有一个角是直角
二.正方形的判定
【考点】正方形的判定.
D
二.正方形的判定
2.如图,在?ABCD中,AC⊥BD于点O,若增加一个条件,使得四边形ABCD是正方形,则下列条件中,不正确的是( )
A.AC=BD
B.AB=BC C.∠ABC=90° D.AO=BO
点拔:
此题主要考查了正方形的判定,
解答此题的关键是熟练掌握正方形的判定定理
B
3.如图所示,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,且DE⊥BC于点E,DF⊥AC于点F,那么四边形CEDF是正方形吗?请说明理由
证明:过D作DG⊥AB,交AB于点G,
∵∠C=∠DEC=∠DFC=90°,
∴四边形CEDF为矩形,
∵AD平分∠CAB,DF⊥AC,DG⊥AB,
∴DF=DG;
∵BD平分∠ABC,DG⊥AB,DE⊥BC,
∴DE=DG,
∴DE=DF,
∴四边形CEDF为正方形.
1.下列对正方形的描述错误的是( )
A.正方形的四个角都是直角
B.正方形的对角线互相垂直
C.邻边相等的矩形是正方形
D.对角线相等的平行四边形是正方形
点拔:
本题考查了正方形的判定与性质、矩形的判定;
熟练掌握正方形的判定与性质是解决问题的关键.
三.正方形综合应用
D
2.如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四种说法:
①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形.
其中,正确的有 (只填写序号)
【考点】
1.正方形的判定
2.平行四边形的判定
3.菱形的判定
4.矩形的判定
①②③④
2.如图,已知E,F,G,H分别是四边形ABCD四边形的中点;
(1)当满足条件 四边形EFGH是矩形;
(2)当满足条件 四边形EFGH是菱形;
(3)当满足条件 四边形EFGH是正方形.
AC⊥BD
AC=BD
AC⊥BD且AC=BD
3.如图,在△ABC
中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACG平分线于点F.?
(1)试说明EO=FO;?
(2)当点O运动到何处时,四边形AECF是矩形?并说明理由.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
3.如图,在△ABC
中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACG平分线于点F.?
(1)试说明EO=FO;
解(1)∵MN∥BC
∴∠OEC=∠BCE
∵CE平分∠BCO
∴∠OCE=∠BCE
∴∠OCE=∠OEC
∴EO=CO
同理可得,FO=CO
∴EO=FO
如图,在△ABC
中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACG平分线于点F.?
(1)试说明EO=FO;?
(2)当点O运动到何处时,四边形AECF是矩形?并说明理由.
(2)当点O运动到AC的中点时,四边形AECF是矩形.
∵当点O运动到AC的中点时,
AO=CO
由(1)得 EO=FO,
∴四边形AECF是平行四边形,
由(1)得 EO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形.
3.如图,在△ABC
中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACG平分线于点F.?
(1)试说明EO=FO;?
(2)当点O运动到何处时,四边形AECF是矩形?并说明理由.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
∵由(2)得,当点O运动到AC的中点时,四边形AECF是矩形,
∵
MN∥BC,
∴
∠ACB
=
∠AOE
当∠ACB=90°时,∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形.
拓展(4)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明,若不是,则说明理由;
(4) 四边形BCFE不可能是菱形,若四边形BCFE为菱形,则 ,,而由(1) 可知 ,在平面内过同一点F不可能有两条直线同垂直于一条直线;
考点:1.平行四边形判定
2.矩形判定
3.菱形判定
4.正方形判定
有关正方形的习题课
优质课比赛内容
一.正方形的性质
1.如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP度数是( )
A.45° B.22.5° C.67.5° D.75°
考查知识点:
1.正方形的对角线平分对角的性质
2.等腰三角形的性质
B
2.如图,在正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E、F,EF=3,则PD的长为( )
A.2 B.3 C. D.6
考查知识点:
1.正方形的性质;
2.全等三角形的判定与性质;
3.矩形的判定与性质
B
3.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .
考查知识点:
1.正方形的性质;
2.直角三角形斜边上的中线;
3.勾股定理;
4.三角形中位线定理.
4.如图,四边形ABCD是边长为a的正方形,点G、E分别是边AB、BC的中点,∠AEF=90°,且EF交正方形外角的平方线CF于点F.
(1)证明:△AGE≌△ECF;
(2)求△AEF的面积.
(1)证明:∵G,E分别是正方形ABCD的边 AB,BC的中点
∴AG=GB=BE=EC
且∠AGE=180°﹣45°=135°
又∵CF是∠DCH的平分线
∴∠DCF=∠FCH=45°
∠ECF=90°+45°=135°
∴在△AGE和△ECF中
∴△AGE≌△ECF
(2)解:由△AGE≌△ECF,得AE=EF;
又∵∠AEF=90°,
∴△AEF是等腰直角三角形;
∵AB=a,E为BC中点,
∴BE= BC= AB= a,
根据勾股定理得:AE= =a,
∴S△AEF= a2.
拓展
条件:点G、E分别是边AB、BC的中点改为点E是边BC的中点,其他条件不变
求证:AE=EF
1.下列条件中,不能判定一个平行四边形是正方形的是( )
A.对角线相等且互相垂直
B.一组邻边相等且有一个角是直角
C.对角线相等且一组邻边相等
D.对角线互相平分且有一个角是直角
二.正方形的判定
【考点】正方形的判定.
D
二.正方形的判定
2.如图,在?ABCD中,AC⊥BD于点O,若增加一个条件,使得四边形ABCD是正方形,则下列条件中,不正确的是( )
A.AC=BD
B.AB=BC C.∠ABC=90° D.AO=BO
点拔:
此题主要考查了正方形的判定,
解答此题的关键是熟练掌握正方形的判定定理
B
3.如图所示,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,且DE⊥BC于点E,DF⊥AC于点F,那么四边形CEDF是正方形吗?请说明理由
证明:过D作DG⊥AB,交AB于点G,
∵∠C=∠DEC=∠DFC=90°,
∴四边形CEDF为矩形,
∵AD平分∠CAB,DF⊥AC,DG⊥AB,
∴DF=DG;
∵BD平分∠ABC,DG⊥AB,DE⊥BC,
∴DE=DG,
∴DE=DF,
∴四边形CEDF为正方形.
1.下列对正方形的描述错误的是( )
A.正方形的四个角都是直角
B.正方形的对角线互相垂直
C.邻边相等的矩形是正方形
D.对角线相等的平行四边形是正方形
点拔:
本题考查了正方形的判定与性质、矩形的判定;
熟练掌握正方形的判定与性质是解决问题的关键.
三.正方形综合应用
D
2.如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四种说法:
①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形.
其中,正确的有 (只填写序号)
【考点】
1.正方形的判定
2.平行四边形的判定
3.菱形的判定
4.矩形的判定
①②③④
2.如图,已知E,F,G,H分别是四边形ABCD四边形的中点;
(1)当满足条件 四边形EFGH是矩形;
(2)当满足条件 四边形EFGH是菱形;
(3)当满足条件 四边形EFGH是正方形.
AC⊥BD
AC=BD
AC⊥BD且AC=BD
3.如图,在△ABC
中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACG平分线于点F.?
(1)试说明EO=FO;?
(2)当点O运动到何处时,四边形AECF是矩形?并说明理由.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
3.如图,在△ABC
中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACG平分线于点F.?
(1)试说明EO=FO;
解(1)∵MN∥BC
∴∠OEC=∠BCE
∵CE平分∠BCO
∴∠OCE=∠BCE
∴∠OCE=∠OEC
∴EO=CO
同理可得,FO=CO
∴EO=FO
如图,在△ABC
中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACG平分线于点F.?
(1)试说明EO=FO;?
(2)当点O运动到何处时,四边形AECF是矩形?并说明理由.
(2)当点O运动到AC的中点时,四边形AECF是矩形.
∵当点O运动到AC的中点时,
AO=CO
由(1)得 EO=FO,
∴四边形AECF是平行四边形,
由(1)得 EO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形.
3.如图,在△ABC
中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACG平分线于点F.?
(1)试说明EO=FO;?
(2)当点O运动到何处时,四边形AECF是矩形?并说明理由.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
∵由(2)得,当点O运动到AC的中点时,四边形AECF是矩形,
∵
MN∥BC,
∴
∠ACB
=
∠AOE
当∠ACB=90°时,∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形.
拓展(4)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明,若不是,则说明理由;
(4) 四边形BCFE不可能是菱形,若四边形BCFE为菱形,则 ,,而由(1) 可知 ,在平面内过同一点F不可能有两条直线同垂直于一条直线;
考点:1.平行四边形判定
2.矩形判定
3.菱形判定
4.正方形判定
