初中数学>>新人教版>>人教版版九年级上册>>第二十五章 概率初步>>随机事件与概率
文档属性
| 名称 | 初中数学>>新人教版>>人教版版九年级上册>>第二十五章 概率初步>>随机事件与概率 |

|
|
| 格式 | rar | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-05-20 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
一块铁放入水中,会不会下沉?
在一定条件下,
必然会发生的事件叫做必然事件。
铁必然会沉入水中,即100%沉入水中。
结论:
跑一百米只用5秒钟,信不信?
绝对不可能,即可能性为0。
一定条件下,
必然不会发生的事件叫做不可能事件。
结论:
买100万张彩票,那么你一定能买到一等奖吗?
买到一等奖有可能发生,也有可能不发生。
在一定条件下,
可能发生也可能不发生的事件叫做随机事件。
结论:
例1 指出下列事件是必然事件,不可能事件,还是随机事件:
(1)某地1月1日刮西北风;
(2)当x是实数是,x2≥0;
(3)手电简的电池没电,灯炮发亮;
(4)一个电影院某天的上座率超过50%.
下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件。
5名同学参加讲演比赛,以抽签方式决定每个人的出场顺序
1.抽到的序号有几种可能的结果?
2.抽到的序号小于6吗?
3.抽到的序号会是0吗?
4.抽到的序号会是1吗?
形状大小相同的签
可能发生也可能不会发生
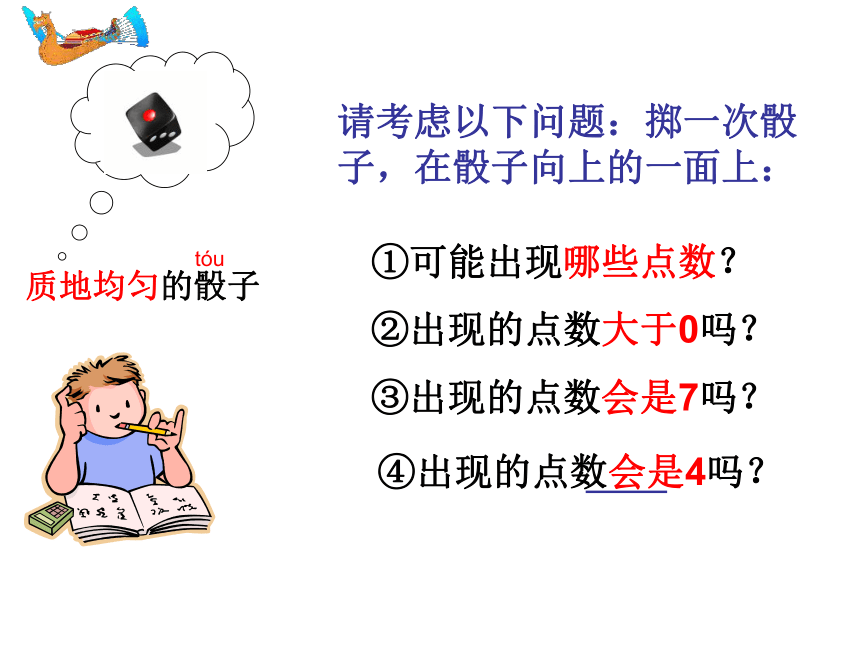
①可能出现哪些点数?
请考虑以下问题:掷一次骰
子,在骰子向上的一面上:
②出现的点数大于0吗?
③出现的点数会是7吗?
④出现的点数会是4吗?
质地均匀的骰子
tóu
是随机事件
2008年奥运会在北京举办!
打开电视正在播刘翔夺冠的体育片
王义夫下一枪会中10环
冠军属于外国选手是不可能事件
冠军属于王楠是随机事件
冠军属于中国是必然事件
我国运动员张怡宁、王楠在最后决赛中会师
冠军属于中国
冠军属于王楠
冠军属于外国选手
(3)掷一枚骰子,向上的一面是6点;
(2)篮球队员在罚线上投篮一次,未投中;
下列事件中,哪些是必然发生的,哪些是不可能发生的,哪些是随机事件。
(1)通常加热到100℃时,水沸腾;
必然事件
随机事件
随机事件
(5)经过城市中某一有交通信号灯的路口,遇到红灯;
(4)度量三角形的内角和,结果是360°;
不可能发生
随机事件
(6)汽车累积行驶1万公里,从未出现故障。
随机事件
相传古代有个王国,国王非常阴险而多疑,一位正直的大臣得罪了国王,被叛死刑,这个国家世代沿袭着一条奇特的法规:凡是死囚,在临刑前都要抽一次“生死签”(写着“生”和“死”的两张纸条),犯人当众抽签,若抽到“死”签,则立即处死,若抽到“生”签,则当众赦免。国王一心想处死大臣,与几个心腹密谋,想出一条毒计:
嘿嘿,这次非让你死不可!
毒计:暗中让执行官把“生死签”上都写成“死”,两死抽一,必死无疑。然而,在断头台前,聪明的大臣迅速抽出一张签纸塞进嘴里,等到执行官反应过来,签纸早已吞下,大臣故作叹息说:“我听天意,将苦果吞下,只要看剩下的签是什么字就清楚了。”剩下的当然写着“死”字,国王怕犯众怒,只好当众释放了大臣。
嘿嘿,这次非让你死不可!
嘿嘿,这次非让你死不可!
老臣自有妙计!
概念巩固
(1)在法规中,大臣被处死是什么事件?
(2)在国王的阴谋中,大臣被处死是什么事件?
(3)在大臣的计策中,大臣被处死是什么事件?
现在有一个盒子,5个红球,4个
白球,每个球除颜色外全部相同。
摸球游戏
问题:1.一次摸出一个球,可能是红球,也可能是白球,,两种可能性一样大吗?
2.那种可能性大,为什么
在同样条件下,随机事件可能发生,也可能不发生,那么它发生的可能性有多大呢?这是我们下面要讨论的问题。
我们从抛掷硬币这个简单问题说起。
实验:让学生以同桌为一小组,每人抛掷50次,记录正面朝上的次数。
概率
抛掷次数(n) 2048 4040 12000 30000 24000
正面朝上数(m) 1061 2048 6019 14984 12012
频率(m/n) 0.518 0.506 0.501 0.4996 0.5005
历史上曾有人作过抛掷硬币的大量重复实验,
结果如下表所示
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
实验结论:
当抛硬币的次数很多时,出现下面的频率值是
稳定的,接近于常数0.5,在它附近摆动.
概率的定义:
一般地,在大量重复进行同一试验时,事件A发生的频率m/n稳定在某个常数p的附近,那么这个常数就叫做事件A的概率,
记作P(A)=P.
必然事件的概率和不可能事件的概率
分别是多少呢?.
P(必然事件)=1
P(不可能事件)=0
记随机事件A在n次试验中发生了m次,那么有0≤m≤n,
0≤m/n≤1
于是可得 0≤P(A) ≤1.
显然,必然事件的概率是1,不可能事件的概率是0.
求概率的方法:
通过大量的重复试验,统计出这个事件的频率近似地作为它的概率。
事件A发生的次数m和试验次数n满足:
0≤m≤n,所以事件A的概率满足
0≤P(A)≤1.
例2:对一批衬衫进行抽查,结果如下表:
抽取件数n 50 100 200 500 800 1000
优等品件数m
42
88
176
445
724
901
优等品频率m/n
0.84
0.88
0.88
0.89
0.901
0.905
求抽取一件衬衫是优等品的概率约是多少?抽取衬衫2000件,约有优质品几件?
某射手进行射击,结果如下表所示:
射击次数n 20 100 200 500 800
击中靶心次数m
13
58
104
255
404
击中靶心频率m/n
(1)填表
(2)这个射手射击一次,击中靶心的概率是多少?
0.5
(3)这射手射击1600次,击中靶心的次数是 。
800
0.65
0.58
0.52
0.51
0.55
有三张牌,抽到J的概率是0.22,抽到Q的概率是0.38,则抽到K的概率是
0.4
大家试验,抛掷一个骰子,它落地时向上的的数为1的概率是多少?
课堂小结:
1、必然事件、不可能事件、随机事件的定义。
2、必然事件A,则P(A)=1;
不可能事件B,则P(B)=0;
随机事件C,则0<P(C)<1。
3、求概率的方法:通过大量反复试验,统计出这件事发生的频率近似地做为它的概率。
4、概率的定义及基本性质。
概率的定义:
一般地,在大量重复进行同一试验时,事件A发生的频率m/n稳定在某个常数p的附近,那么这个常数就叫做事件A的概率,
记作P(A)=P.
0≤P(A) ≤1.
必然事件的概率是1,不可能事件的概率是0.
一块铁放入水中,会不会下沉?
在一定条件下,
必然会发生的事件叫做必然事件。
铁必然会沉入水中,即100%沉入水中。
结论:
跑一百米只用5秒钟,信不信?
绝对不可能,即可能性为0。
一定条件下,
必然不会发生的事件叫做不可能事件。
结论:
买100万张彩票,那么你一定能买到一等奖吗?
买到一等奖有可能发生,也有可能不发生。
在一定条件下,
可能发生也可能不发生的事件叫做随机事件。
结论:
例1 指出下列事件是必然事件,不可能事件,还是随机事件:
(1)某地1月1日刮西北风;
(2)当x是实数是,x2≥0;
(3)手电简的电池没电,灯炮发亮;
(4)一个电影院某天的上座率超过50%.
下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件。
5名同学参加讲演比赛,以抽签方式决定每个人的出场顺序
1.抽到的序号有几种可能的结果?
2.抽到的序号小于6吗?
3.抽到的序号会是0吗?
4.抽到的序号会是1吗?
形状大小相同的签
可能发生也可能不会发生
①可能出现哪些点数?
请考虑以下问题:掷一次骰
子,在骰子向上的一面上:
②出现的点数大于0吗?
③出现的点数会是7吗?
④出现的点数会是4吗?
质地均匀的骰子
tóu
是随机事件
2008年奥运会在北京举办!
打开电视正在播刘翔夺冠的体育片
王义夫下一枪会中10环
冠军属于外国选手是不可能事件
冠军属于王楠是随机事件
冠军属于中国是必然事件
我国运动员张怡宁、王楠在最后决赛中会师
冠军属于中国
冠军属于王楠
冠军属于外国选手
(3)掷一枚骰子,向上的一面是6点;
(2)篮球队员在罚线上投篮一次,未投中;
下列事件中,哪些是必然发生的,哪些是不可能发生的,哪些是随机事件。
(1)通常加热到100℃时,水沸腾;
必然事件
随机事件
随机事件
(5)经过城市中某一有交通信号灯的路口,遇到红灯;
(4)度量三角形的内角和,结果是360°;
不可能发生
随机事件
(6)汽车累积行驶1万公里,从未出现故障。
随机事件
相传古代有个王国,国王非常阴险而多疑,一位正直的大臣得罪了国王,被叛死刑,这个国家世代沿袭着一条奇特的法规:凡是死囚,在临刑前都要抽一次“生死签”(写着“生”和“死”的两张纸条),犯人当众抽签,若抽到“死”签,则立即处死,若抽到“生”签,则当众赦免。国王一心想处死大臣,与几个心腹密谋,想出一条毒计:
嘿嘿,这次非让你死不可!
毒计:暗中让执行官把“生死签”上都写成“死”,两死抽一,必死无疑。然而,在断头台前,聪明的大臣迅速抽出一张签纸塞进嘴里,等到执行官反应过来,签纸早已吞下,大臣故作叹息说:“我听天意,将苦果吞下,只要看剩下的签是什么字就清楚了。”剩下的当然写着“死”字,国王怕犯众怒,只好当众释放了大臣。
嘿嘿,这次非让你死不可!
嘿嘿,这次非让你死不可!
老臣自有妙计!
概念巩固
(1)在法规中,大臣被处死是什么事件?
(2)在国王的阴谋中,大臣被处死是什么事件?
(3)在大臣的计策中,大臣被处死是什么事件?
现在有一个盒子,5个红球,4个
白球,每个球除颜色外全部相同。
摸球游戏
问题:1.一次摸出一个球,可能是红球,也可能是白球,,两种可能性一样大吗?
2.那种可能性大,为什么
在同样条件下,随机事件可能发生,也可能不发生,那么它发生的可能性有多大呢?这是我们下面要讨论的问题。
我们从抛掷硬币这个简单问题说起。
实验:让学生以同桌为一小组,每人抛掷50次,记录正面朝上的次数。
概率
抛掷次数(n) 2048 4040 12000 30000 24000
正面朝上数(m) 1061 2048 6019 14984 12012
频率(m/n) 0.518 0.506 0.501 0.4996 0.5005
历史上曾有人作过抛掷硬币的大量重复实验,
结果如下表所示
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
实验结论:
当抛硬币的次数很多时,出现下面的频率值是
稳定的,接近于常数0.5,在它附近摆动.
概率的定义:
一般地,在大量重复进行同一试验时,事件A发生的频率m/n稳定在某个常数p的附近,那么这个常数就叫做事件A的概率,
记作P(A)=P.
必然事件的概率和不可能事件的概率
分别是多少呢?.
P(必然事件)=1
P(不可能事件)=0
记随机事件A在n次试验中发生了m次,那么有0≤m≤n,
0≤m/n≤1
于是可得 0≤P(A) ≤1.
显然,必然事件的概率是1,不可能事件的概率是0.
求概率的方法:
通过大量的重复试验,统计出这个事件的频率近似地作为它的概率。
事件A发生的次数m和试验次数n满足:
0≤m≤n,所以事件A的概率满足
0≤P(A)≤1.
例2:对一批衬衫进行抽查,结果如下表:
抽取件数n 50 100 200 500 800 1000
优等品件数m
42
88
176
445
724
901
优等品频率m/n
0.84
0.88
0.88
0.89
0.901
0.905
求抽取一件衬衫是优等品的概率约是多少?抽取衬衫2000件,约有优质品几件?
某射手进行射击,结果如下表所示:
射击次数n 20 100 200 500 800
击中靶心次数m
13
58
104
255
404
击中靶心频率m/n
(1)填表
(2)这个射手射击一次,击中靶心的概率是多少?
0.5
(3)这射手射击1600次,击中靶心的次数是 。
800
0.65
0.58
0.52
0.51
0.55
有三张牌,抽到J的概率是0.22,抽到Q的概率是0.38,则抽到K的概率是
0.4
大家试验,抛掷一个骰子,它落地时向上的的数为1的概率是多少?
课堂小结:
1、必然事件、不可能事件、随机事件的定义。
2、必然事件A,则P(A)=1;
不可能事件B,则P(B)=0;
随机事件C,则0<P(C)<1。
3、求概率的方法:通过大量反复试验,统计出这件事发生的频率近似地做为它的概率。
4、概率的定义及基本性质。
概率的定义:
一般地,在大量重复进行同一试验时,事件A发生的频率m/n稳定在某个常数p的附近,那么这个常数就叫做事件A的概率,
记作P(A)=P.
0≤P(A) ≤1.
必然事件的概率是1,不可能事件的概率是0.
同课章节目录
