解直角三角形应用
图片预览


文档简介
(共17张PPT)
解直角三角形的应用:
利用解直角三角形解测量、航海、工程技术和物理学中的有关距离、高度、角度即仰角俯角;方向角或方位角;坡度、坡角、水平距离,垂直距离等问题是现今中考的热点。 (1)应用中要弄明白它们的概念,理解题目所述的实际意义,弄清已测与所求之间的关系,能根据题意正确画图或识图,从图中确定要解的直角三角形,解直角三角形时,充分使用原始数据,正确选择关系式,使运算尽可能简便、准确。
(2)、如果图中无直角三角形,可适当地作垂线,转化为直角三角形,间接地解出。
(3)、在解一些较复杂图形时,注意借助于几何图形的性质,可使得问题得到解决。
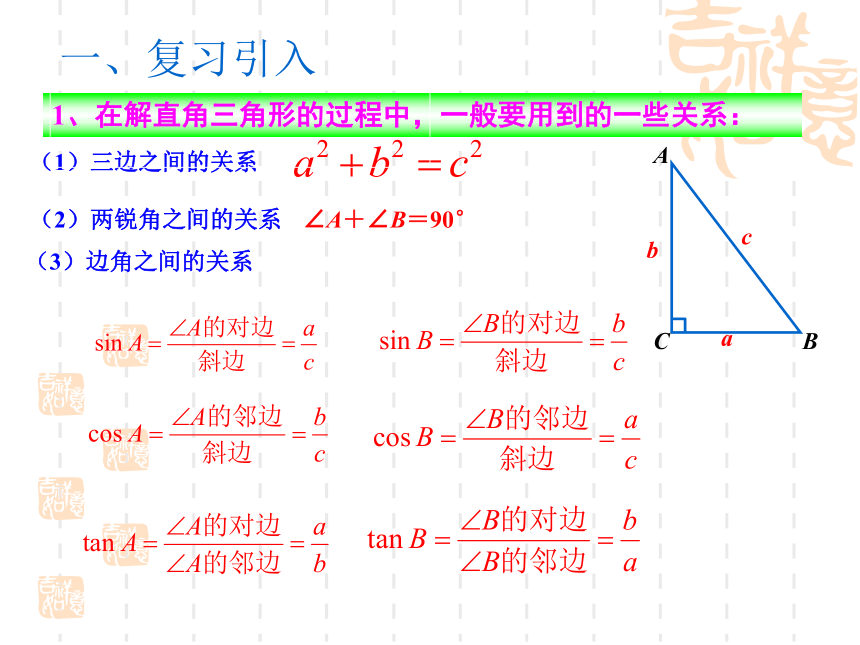
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
1、在解直角三角形的过程中,一般要用到的一些关系:
一、复习引入
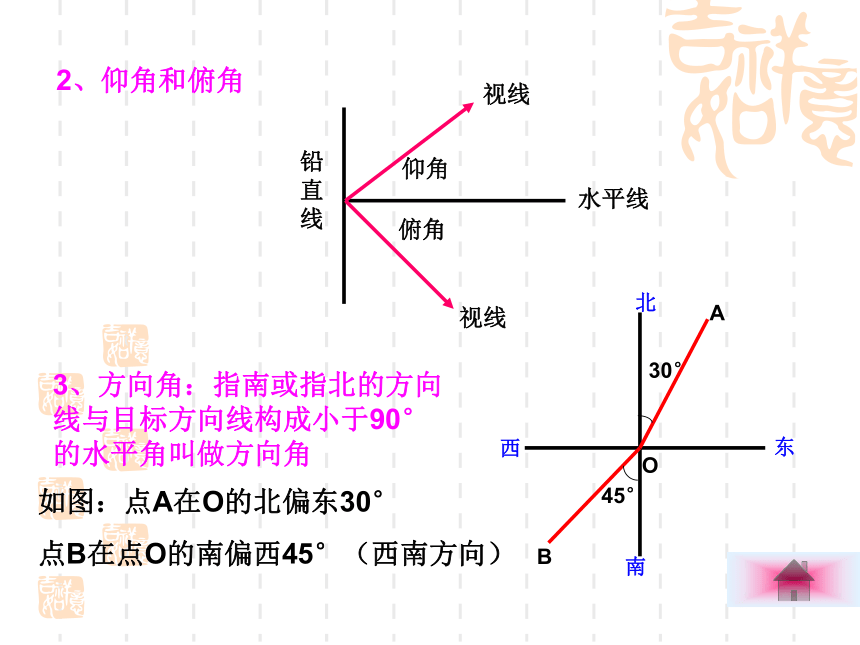
2、仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
3、方向角:指南或指北的方向线与目标方向线构成小于90°的水平角叫做方向角
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
30°
45°
B
O
A
东
西
北
南
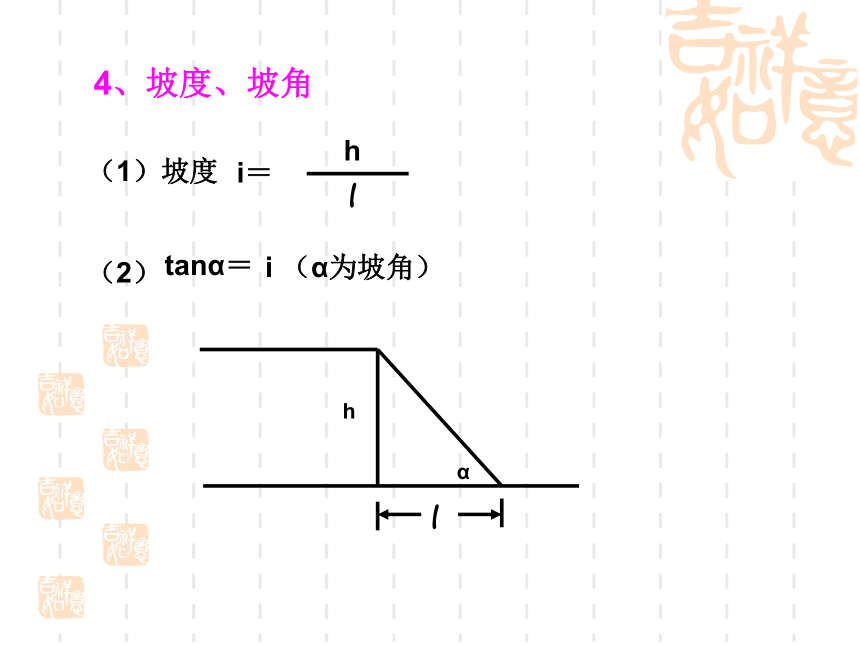
4、坡度、坡角
l
h
α
(1)坡度
i=
h
l
tanα=
i
(α为坡角)
(2)
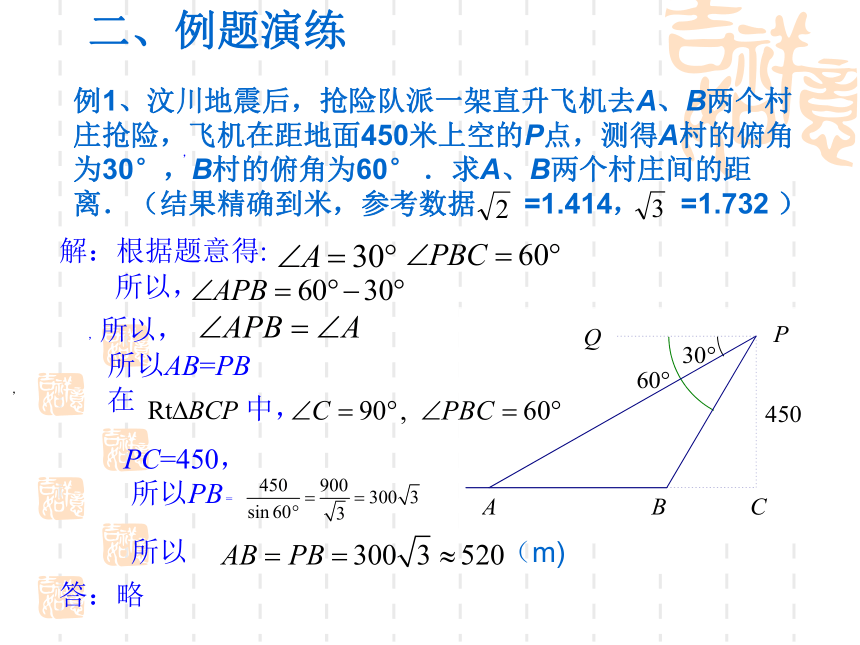
例1、汶川地震后,抢险队派一架直升飞机去A、B两个村庄抢险,飞机在距地面450米上空的P点,测得A村的俯角为30°,B村的俯角为60° .求A、B两个村庄间的距离.(结果精确到米,参考数据 =1.414, =1.732 )
二、例题演练
,
解:根据题意得:
,
所以,
,所以,
所以AB=PB
在
中,
PC=450,
所以PB =
所以
答:略
(m)
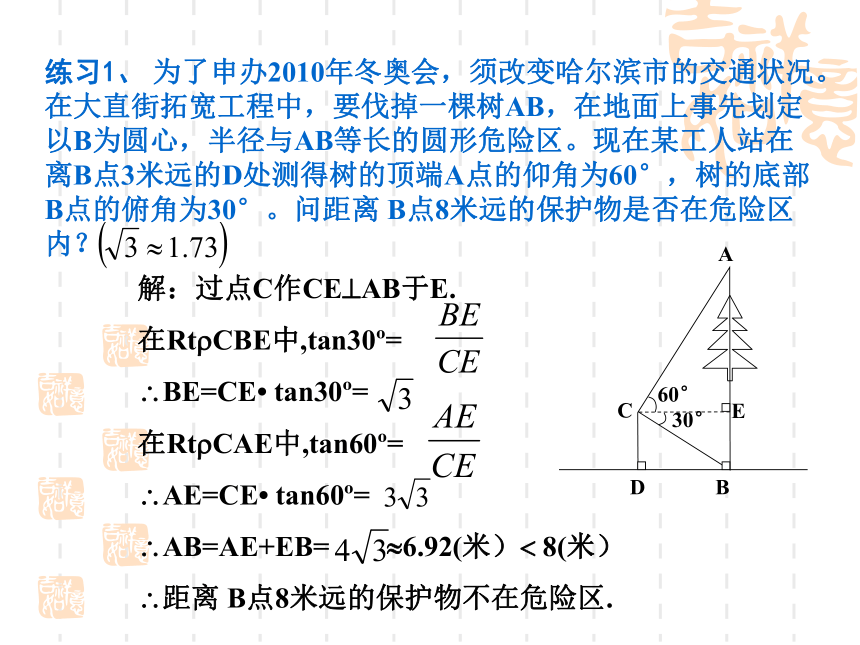
练习1、 为了申办2010年冬奥会,须改变哈尔滨市的交通状况。在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区。现在某工人站在离B点3米远的D处测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°。问距离 B点8米远的保护物是否在危险区内?
C
D
B
E
30°
60°
A
解:过点C作CE AB于E.
在Rt CBE中,tan30 =
BE=CE tan30 =
在Rt CAE中,tan60 =
AE=CE tan60 =
AB=AE+EB= 6.92(米) 8(米)
距离 B点8米远的保护物不在危险区.
例2、(2008山东青岛)一艘轮船自西向东航行,在A处测得东偏北21.3°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北63.5°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?(参考数据:sin21.3°≈9/25,tan21.3°≈2/5, sin63.5°≈9/10,tan63.5°≈2)
东
北
68.7°
D
解:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD.
设BD=x海里,
在Rt△BCD中,tan∠CBD=CD/BD,
∴CD=x ·tan63.5°.
在Rt△ACD中,AD=AB+BD=(60+x)海里,tan∠A=CD/AD,
∴CD=( 60+x ) ·tan21.3°.
∴x·tan63.5°=(60x)·tan21.3,
解得,x=15.
练习2、外国船只,除特许外,不得进入我国海洋100海里以内的区域.如图,设A、B是我们的观察站,A和B之间的距离为160海里,海岸线是过A、B的一条东西直线.一外国船只在P点,在A点测得北偏东450,同时在B点测得北偏西300,问此时是否要向外国船只发出警告,令其退出我国海域.
A
B
P
⌒
⌒
45°
60°
┓
C
例3、一段河坝的横断面为等腰三角形ABCD,试根据下图中的数据求出坡角α和坝底宽AD。(单位是米,结果保留根号)
A
B
C
D
E
F
4
6
α
练习3拦水坝横断面为梯形ABCD(图中i=1: 是指坡面的铅直高度AF与水平宽度BF的比)根据图中数据求: (1)坡角α和β. (2)斜坡AB的长.
B
A
C
D
E
F
α
β
i=1:
i=1:1
6m
谈谈今天的收获
三、小结
1、应用解直角三角形的知识解决实际问题时要注意:当已知条件或求解中有斜边时,用正弦或余弦,无斜边,用正切;计算结果的精确度要求,一般来说中间量要多取一位有效数字;在题目中求未知量时,应尽量选用直接由已知量求未知量;当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线),再用直角三角形中的边角关系解决。
2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
四、作业:
见 教科书第97页第9、10题
解直角三角形的应用:
利用解直角三角形解测量、航海、工程技术和物理学中的有关距离、高度、角度即仰角俯角;方向角或方位角;坡度、坡角、水平距离,垂直距离等问题是现今中考的热点。 (1)应用中要弄明白它们的概念,理解题目所述的实际意义,弄清已测与所求之间的关系,能根据题意正确画图或识图,从图中确定要解的直角三角形,解直角三角形时,充分使用原始数据,正确选择关系式,使运算尽可能简便、准确。
(2)、如果图中无直角三角形,可适当地作垂线,转化为直角三角形,间接地解出。
(3)、在解一些较复杂图形时,注意借助于几何图形的性质,可使得问题得到解决。
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
1、在解直角三角形的过程中,一般要用到的一些关系:
一、复习引入
2、仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
3、方向角:指南或指北的方向线与目标方向线构成小于90°的水平角叫做方向角
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
30°
45°
B
O
A
东
西
北
南
4、坡度、坡角
l
h
α
(1)坡度
i=
h
l
tanα=
i
(α为坡角)
(2)
例1、汶川地震后,抢险队派一架直升飞机去A、B两个村庄抢险,飞机在距地面450米上空的P点,测得A村的俯角为30°,B村的俯角为60° .求A、B两个村庄间的距离.(结果精确到米,参考数据 =1.414, =1.732 )
二、例题演练
,
解:根据题意得:
,
所以,
,所以,
所以AB=PB
在
中,
PC=450,
所以PB =
所以
答:略
(m)
练习1、 为了申办2010年冬奥会,须改变哈尔滨市的交通状况。在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区。现在某工人站在离B点3米远的D处测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°。问距离 B点8米远的保护物是否在危险区内?
C
D
B
E
30°
60°
A
解:过点C作CE AB于E.
在Rt CBE中,tan30 =
BE=CE tan30 =
在Rt CAE中,tan60 =
AE=CE tan60 =
AB=AE+EB= 6.92(米) 8(米)
距离 B点8米远的保护物不在危险区.
例2、(2008山东青岛)一艘轮船自西向东航行,在A处测得东偏北21.3°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北63.5°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?(参考数据:sin21.3°≈9/25,tan21.3°≈2/5, sin63.5°≈9/10,tan63.5°≈2)
东
北
68.7°
D
解:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD.
设BD=x海里,
在Rt△BCD中,tan∠CBD=CD/BD,
∴CD=x ·tan63.5°.
在Rt△ACD中,AD=AB+BD=(60+x)海里,tan∠A=CD/AD,
∴CD=( 60+x ) ·tan21.3°.
∴x·tan63.5°=(60x)·tan21.3,
解得,x=15.
练习2、外国船只,除特许外,不得进入我国海洋100海里以内的区域.如图,设A、B是我们的观察站,A和B之间的距离为160海里,海岸线是过A、B的一条东西直线.一外国船只在P点,在A点测得北偏东450,同时在B点测得北偏西300,问此时是否要向外国船只发出警告,令其退出我国海域.
A
B
P
⌒
⌒
45°
60°
┓
C
例3、一段河坝的横断面为等腰三角形ABCD,试根据下图中的数据求出坡角α和坝底宽AD。(单位是米,结果保留根号)
A
B
C
D
E
F
4
6
α
练习3拦水坝横断面为梯形ABCD(图中i=1: 是指坡面的铅直高度AF与水平宽度BF的比)根据图中数据求: (1)坡角α和β. (2)斜坡AB的长.
B
A
C
D
E
F
α
β
i=1:
i=1:1
6m
谈谈今天的收获
三、小结
1、应用解直角三角形的知识解决实际问题时要注意:当已知条件或求解中有斜边时,用正弦或余弦,无斜边,用正切;计算结果的精确度要求,一般来说中间量要多取一位有效数字;在题目中求未知量时,应尽量选用直接由已知量求未知量;当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线),再用直角三角形中的边角关系解决。
2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
四、作业:
见 教科书第97页第9、10题
